PROBLEM LINK:
Editorialist: Soumik Sarkar
DIFFICULTY:
MEDIUM
PREREQUISITES:
2D geometry, Dynamic programming, Sorting, Binary search
PROBLEM:
Given a list of n points on a 2D plane such that no two have the same x-coordinate, find the length of the longest sequence of points p_1, p_2, ... p_k such that x_{p_1}, x_{p_2}, ... x_{p_k} is in increasing order and each point p_i for 3 \le i \le k lies below or on the line joining points p_{i-1} and p_{i-2}.
EXPLANATION:
First let us sort the points by their x-coordinate since the sequence as required by the problem must be in increasing order of x-coordinate. We are also considering 0-based indexing. Now suppose we are at the i^{th} point P_i which is the last point in some sequence as required by the problem. At P_i, we can choose any P_j given j < i to be the second last point. However, the third last point P_k must be such that P_i lies below the line joining P_j and P_k. Take a look at the situation below.
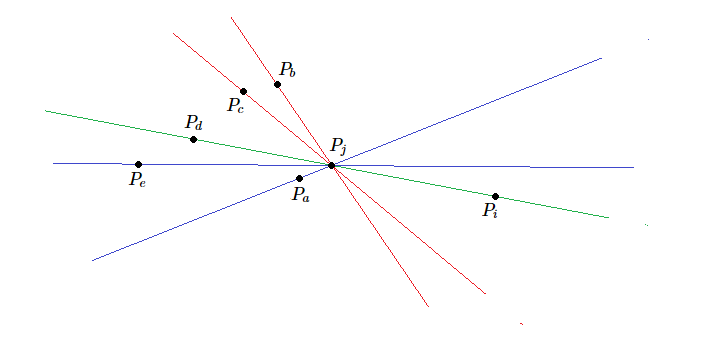
P_b and P_c cannot be chosen as P_k, but P_a, P_d, P_e are valid choices for P_k.
Let f(i, j) be the largest sequence as required by the problem, whose last point is P_i and the second last is P_j. Of course 0 \le i, j < n and j < i. Then,
Comparing the slopes is a simple way to determine whether P_i lies below or on the point joining P_j and P_k. The answer will be the maximum f(i, j) over all i, j. So now we have a correct \mathcal{O}(n^3) solution. However this is not fast enough, and we must improve it.
Notice that we are choosing all k such that some parameter that depends on k is greater than a threshold value. Along with some dp[j][k] which stores f(j, k), let’s have another structure C where C[j] is a list of pairs of values (k, f(j, k)). Now if the pairs in C[j] are sorted by slope(P_j, P_k), then from point i we can use binary search get some index in C[j] beyond which all are valid choices of the third last point! Let this index be b, then we only need to choose the max of all values f(j, k) from each pair in C[j] from index b to the end of C[j]. We can use a suffix max array S[j] to precalculate these max values from any index till the end. The complexity has been reduced to \mathcal{O}(n^2 \log n).
Some things to note:
- The dp table is now redundant, just using C is enough.
- Instead of storing (k, f(j, k)) pairs we can store (slope(P_j, P_k), f(j, k)) pairs for convenience, especially in C++ which has built-in support for ordering pairs (Python does too but sadly it is too slow to clear the given time limit).
- We can add a sentinel pair (\infty, 1) to each C[j] to denote the sequence with the point P_j by itself. Without this, we would have to separately handle empty binary search results.
Refer to the editorialist’s solution for better understanding.
EDITORIALIST’S SOLUTION:
Editorialist’s solution can be found here.