PROBLEM LINK:
Setter- Karthik Singhal
Tester- Suchan Park
Editorialist- Abhishek Pandey
DIFFICULTY:
Easy
PRE-REQUISITES:
Properties of XOR , Basic Math to make up the formula.
PROBLEM:
Given an array A of size N, find number of triplets (i,j,k), i < j \leq k such that XOR of subarray from [i,j-1] is equal to XOR of subarray [j,k].
QUICK-EXPLANATION:
Key to AC- If XOR of a subarray of length L is 0, then there are L-1 valid triplets.
Realize that A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} = A_j \oplus A_{j+1} \oplus .... \oplus A_k, on re-arranging the terms becomes A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k =0 , i.e. the XOR of subarray in range [i,k] must be 0.
Lets say that we find such a subarray of length L. Then, it will contribute L-1 pairs to the answer, as if the XOR of a subarray is 0, then we can place j anywhere i \leq j \leq k and get a valid triplet. Since j cannot be equal to i, hence 1 is subtracted.
Now, to compute the answer efficiently, we will use prefix XOR. If we see that the prefix XOR at 2 indices, say L and R, is same - then it means that the XOR of subarray [L+1,R] is 0. Hence, we make a list which tells that what prefix value occurs at what indices. Now, multiple methods are there which will lead to different forms of same formula or computation, one of them being-
Assuming that we are currently at index i, where prefix xor is S, keep track of following variables :
- cnt[S]- Number of times this prefix-xor S is seem before index i.
- bad\_ways[S]- For every index j such that j<i and prefix XOR at j is also equal to S, add (j+1) to the number of bad ways.
These variables affect answer in following way -
Ans=Ans+ cnt[S]*i-bad\_ways[S] for all i (1-based indexing)
EXPLANATION:
We will divide the editorial into 3 sections.
- Proof 1 that A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} = A_j \oplus A_{j+1} \oplus .... \oplus A_k, on re-arranging the terms becomes A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k =0
- Proof 2 that such a subarray (of length, say L) contributes L-1 to the answer.
- Derivation of formula for final answer.
Proof 1
This will be the shortest proof. Here, we will use the property of XOR that-
“A number, if XOR’ed with itself, results in 0. Meaning X \oplus X=0. Also, a number when XOR’ed with 0 yields itself. That is, 0 \oplus X=X”
We have-
A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} = A_j \oplus A_{j+1} \oplus .... \oplus A_k
XORING with A_j \oplus A_{j+1} \oplus .... \oplus A_k on both sides-
A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k= A_j \oplus A_{j+1} \oplus .... \oplus A_k \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k
\implies A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k= (A_j \oplus A_j) \oplus (A_{j+1} \oplus A_{j+1}) \oplus .... \oplus (A_k \oplus A_k)
\implies A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k = 0 \oplus 0 \oplus ... \oplus 0
\therefore A_i \oplus A_{i+1} \oplus .... \oplus A_{j-1} \oplus A_j \oplus A_{j+1} \oplus .... \oplus A_k =0
\implies XOR of subarray in range [i,k] is 0.
Proof 2
Now we know that for every such triplet (i,j,k), the XOR of subarray in range [i,k] is 0. This gives a good insight to the problem.
One thing which we should think right now is, that, what does the problem reduces to now?
What some people wrongly assume is, that now the answer is count of subarrays with XOR 0. But it is not true, because as we will see below, a subarray can contribute multiple triplets to the answer!
How so? Easy, just read the below theorem properly-
“If the XOR of a subarray in range [L,R] is 0, then we can always divide this subarray into 2 subarrays [L,i] and [i,R] \forall L \leq i \leq R such that XOR of both these subarrays is equal.”
Lets prove it now. The proof is easy, using the property that X \oplus X=0 and that 0 \oplus X=X again. You may want to stop here if you want to do the proof yourself.
Proof-
Given that-
A_L \oplus A_{L+1} \oplus ... \oplus A_R=0.
Let me take an index i such that L \leq i \leq R. XORING both sides with A_L \oplus A_{L+1} \oplus ... \oplus A_i, we get-
A_L \oplus A_{L+1} \oplus ... \oplus A_R \oplus (A_L \oplus A_{L+1} \oplus ... \oplus A_i) = 0 \oplus (A_L \oplus A_{L+1} \oplus ... \oplus A_i)
(A_L \oplus A_L) \oplus ...\oplus (A_i \oplus A_i) \oplus A_{i+1} \oplus ... \oplus A_R = A_L \oplus A_{L+1} \oplus ... \oplus A_i
\implies 0 \oplus ... \oplus 0 \oplus A_{i+1} \oplus ... \oplus A_R = A_L \oplus A_{L+1} \oplus ... \oplus A_i
\therefore A_{i+1} \oplus ... \oplus A_R = A_L \oplus A_{L+1} \oplus ... \oplus A_i
OR
A_L \oplus A_{L+1} \oplus ... \oplus A_i = A_{i+1} \oplus ... \oplus A_R
Now, note that the length of a subarray is just the number of elements in it. A subarray from [L,R] has length R-L+1. Now, read the incoming paragraph(s) carefully.
For our current question, we need to find how many triplets (i,j,k) a subarray from [L,R] contributes. Note that for the subarray under consideration, i=L and k=R are fixed (as changing them would mean changing the subarray. Since we are talking about contribution of a particular subarray right now, i and k are fixed).
Now, j ideally could have taken any value between [L,R] and we would have XOR of subarray [L,j] equal to XOR of subarray from [j,R]. That would be R-L+1 values. But j=i is not allowed by the question. Hence, number of possible values j can take reduces by 1. Hence, R-L triplets are contributed by this subarray.
Expressing them in terms of length of subarray (because we talked in terms of length earlier in quick explanation)-
Length = R-L+1
Triplets = R-L = Length -1.
Hence, if the length of the subarray is L, then L-1 triplets are possible.
Deriving the final formula
In previous proof, we saw that if the subarray of length L as XOR 0, then it contributes L-1 triplets to the answer.
Now, the first step before deriving the formal answer is to identify subarrays with XOR 0. How will we efficiently find this out?
The standard trick used here is to use prefix XOR. Let pref[i] denote A_1 \oplus ... \oplus A_i, i.e. the prefix XOR till i. Now, say that I have 2 indices, i and j such that pref[i]==pref[j]. Then this means that the XOR of subarray in range [i+1,j] is 0.
If you want the proof or intuition for it, you can refer below-
Proof
pref[i] = pref[j]
\implies A_1 \oplus ... \oplus A_i = A_1 \oplus ... \oplus A_i \oplus A_{i+1} \oplus ... \oplus A_j
XORING both sides with A_1 \oplus ... \oplus A_i
(A_1 \oplus ... \oplus A_i) \oplus (A_1 \oplus ... \oplus A_i) = (A_1 \oplus A_1) \oplus ... \oplus (A_i \oplus A_i) \oplus A_{i+1} \oplus ... \oplus A_j
\implies A_{i+1} \oplus ... \oplus A_j =0
This gives us a big hint! The answer lies in keeping the track of the previous values of prefix-XOR encountered!
Before proceeding forward, I’d like to recall that if a subarray of XOR 0 has length L, it contributes L-1 triplets to the answer.
Now, say I am iterating through the prefix-XOR array pref[]. Say I have pref[i]=S right now. All I need to do is, to iterate over all j such that j<i and pref[i]=pref[j]. For all such j, I add i-j to the answer. But this is O(N^2). How to improve it?
Easy! Precomputation!
Since I do not want that we get lost in conventions or variables used, let me define things as follow-
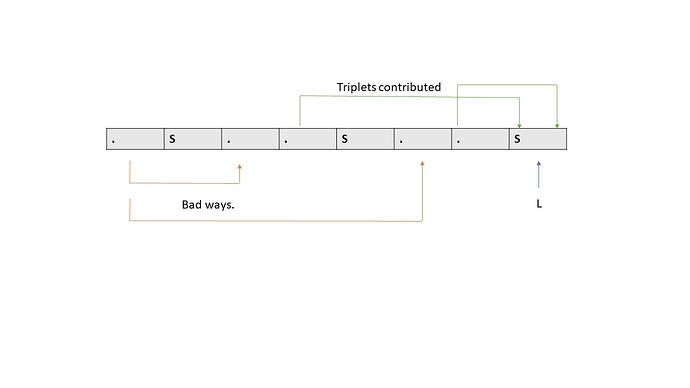
Say we are iterating the prefix-XOR array, and are currently at index R such that pref[R]=S. Lets consider contribution of all subarrays ending at R. For every i such that i<R and pref[i]=pref[R]=S, we know that the XOR of subarray from range [i+1,R] has XOR 0, and contributes R-(i+1) to the answer.
This is the first hint! For every i where we find pref[i]=S , we add (i+1) to number of bad\_ways for prefix-XOR S. In other words, we just make an array bad\_ways[] and perform bad\_ways[S]+=(i+1).
Now, say number of times I encountered prefix XOR of S so far (i.e. till index R) is cnt. Now, I can find answer as-
Triplets += cnt*R-bad \_ ways[S]
Confused how this came from? You can see it below!
How did we get above?
Contribution \ at \ index \ R = \sum [R - (i+1) ] for all i such that pref[i]=pref[R]=S
\sum [R - (i+1) ] = cnt * R - \sum (i+1) since we know that S occurred cnt times before, and hence there are cnt such i.
\implies \sum [R - (i+1) ]= cnt*R - bad\_ways[S] as bad\_ways[S] stores the \sum (i+1) on coming across such an index i.
To get an intuition of the above formula, you can refer to image below-
SOLUTION
Setter
#include<bits/stdc++.h>
#include <chrono>
using namespace std;
using namespace std::chrono;
#define ll long long
vector<ll>v[2000005];
int main()
{
//auto start = high_resolution_clock::now();
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// ifstream inn;
// inn.open("input8.txt");
// if (!inn) {
// cerr << "Unable to open file datafile.txt";
// exit(1); // call system to stop
// }
// ofstream my;
// my.open("output8.txt");
ll t;
cin >> t;
while(t--)
{
for(int i=0;i<2000005;i++)
v[i].clear();
ll n;
cin >> n;
ll arr[n];
for(ll i=0;i<n;i++)
cin >>arr[i];
v[0].push_back(0);
ll z=0;
ll ans=0;
for(ll i=0;i<n;i++)
{
z=z^arr[i];
v[z].push_back(i+1);
}
for(ll i=0;i<2000005;i++)
{
for(ll j=0;j<v[i].size();j++)
{
ans+=v[i][j]*(j-(v[i].size()-1-j));
}
ans=ans-(v[i].size()*(v[i].size()-1))/2;
}
cout << ans<<"\n";
//my << ans<<endl;
}
//inn.close();
// auto stop = high_resolution_clock::now();
// auto duration = duration_cast<microseconds>(stop - start);
// cout << duration.count() << endl;
}
Tester
fun main(Args: Array<String>) {
repeat(readLine()!!.toInt()) {
val N = readLine()!!.toInt()
val A = listOf(0) + readLine()!!.trim().split(" ").map{ it.toInt() }
val P = run { var acc = 0; A.map{ acc = acc xor it; acc } }
// P[j-1] xor P[i-1] = P[k-1] xor P[j-1] -> P[i-1] = P[k-1] (k - i)
val pref = mutableMapOf<Int, Pair<Long, Long>>()
var ans = 0L
for((k, v) in P.withIndex()) {
val (icount, isum) = pref.getOrDefault(v, Pair(0L, 0L))
ans += icount * (k-1) - isum
pref[v] = Pair(icount + 1, isum + k)
}
println(ans)
}
}
A solution using editorial's approach
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
namespace io
{
const int N=1<<20;
char buf[N],*t1=buf,*t2=buf;
#ifdef cjy
#define getc getchar
#else
#define getc() t1==t2&&(t2=(t1=buf)+fread(buf,1,N,stdin),t1==t2)?EOF:*t1++
#endif
inline int read()
{
static int an;an=0;
static char ch;ch=getc();
while(ch<48||ch>57)ch=getc();
while(ch>=48&&ch<=57)an=(an<<3)+(an<<1)+(ch^48),ch=getc();
return an;
}
}using io::read;
int T,n,a[100010];
int cnt[2000020];
long long sum[2000020],ans;
int main()
{
T=read();
cnt[0]=1;sum[0]=1;
while(T--)
{
n=read();
int s=0;ans=0;
for(int i=1;i<=n;++i)
{
a[i]=read();
s^=a[i];
ans+=1ll*cnt[s]*i-sum[s];
++cnt[s];
sum[s]+=i+1;
}
printf("%lld\n",ans);
s=0;
for(int i=1;i<=n;++i)
{
s^=a[i];
--cnt[s];
sum[s]-=i+1;
}
}
return 0;
}
The credits for above solution go to cjy2003
Time Complexity=O(N)
Space Complexity=O(N)
CHEF VIJJU’S CORNER 
-
Expand the solution for 0 \leq A_i \leq 10^{18}. Discuss the following points for your solution-
- What data structures did you use?
- Is the complexity same as before or did it increase?
- Will it work for -10^{18} \leq A_i \leq 10^{18}
-
Prove of disprove the following-
- The editorial states that a subarray, whose XOR is 0, can always be divided into 2 subarrays with equal XOR. With that in mind, can I propose that-
- Such a subarray (whose XOR is 0) can be divided into 2 subsets with equal XOR?
- Can I propose that no matter HOW I distribute elements into those 2 subsets, they will always have equal XOR?
- Can I extend it to K subsets?
- The editorial states that a subarray, whose XOR is 0, can always be divided into 2 subarrays with equal XOR. With that in mind, can I propose that-
-
Prove or disprove the method of computation given below. PS: Proof by AC or Proof by WA are not accepted
 .
.- Say my prefix xor S repeats at indices i_1,i_2,...,i_n. Now, for each such index i_x, I will see how many times prefix xor of S occurs AFTER i_x. Let it be cnt. Now, I will see the difference between i_{x+1} and i_x. These many elements contribute cnt times to the final answer, hence I will add cnt*(i_{x+1}-i_x) to the answer. Doing this for all indices, and for all prefix XOR S, I will get final answer.
Setter's Notes
As in the given problem, we have to find all the triplets (i,j,k) such that Arr[i]^Arr[i+1}^…Arr[j-1]=Arr[j]^Arr[j+1]^…Arr{k].
The brute force solution is very easy in O(n^3) i.e to iterate over all the subarrays & see where this condition is satisfied and add it to the answer.
Now trying to optimize it , we can do better i.e in O(n^2), what we can do is we can precompute the value of xors in a prefix array and use this array in iterating over all the subarrays and this reduces one loop for calculating xors .
Can we do more better, Yes we can do it in O(n).
Now here comes a little bit of bit manipulation, If we have an array of integers and the total xor all the elements is 0 then at whatever position i break the array into two parts the xor of the two halves will be equal.
Example : 6 5 1 2
Where ever i break this array the zor of the two halves will be same as the overall xor the array is 0 ( in this case the size of array is 4 and the number of possible positions where i can break this array is 3 )
So now i think you all know what you all have to do i.e see which subarrays of the array have xor zero.
This can be achieved by taking prefix xor of the array and storing all the positions of particular xor value.
Now we know that between which indices the xor is zero i.e between all the pairs of the indices of a particular xor value.
Assume that for some array the prefix xor is having value 3 at 4 different positions.
Let the positions be 2 5 7 11 now we need to consider all the pairs of these indices and find the difference between then because these will be the positions where we can break the corresponding subarrays, that can be done in O(n^2).
Here comes a little maths and you can refer to editorial to know how to do it in O(n) :D.
And finally add up all the differences for all different xor values, that will be our final answer.