PROBLEM LINK:
Author: Sunny Aggarwal
Tester: Sergey Kulik
Editorialist: Sunny Aggarwal
DIFFICULTY:
Medium
PRE-REQUISITES:
Trees, Dynamic Programming, Memoization, Implementation, Observation.
PROBLEM STATEMENT:
You are given a tree T and 2 integers K and M. You are asked to count the number of ways of assigning an integer to each node from range [1, M] such that absolute difference between the integers assigned to adjacent pairs of nodes is atleast K.
SOLUTION:
Subtask 1:
Number of ways of assigning an integer (say y) to a node (say x) such that subtree rooted at node x holds the desire properties can be computed using following recurrence
C++ Code:
const int maxN = 111;
const int maxM = 111;
const int mod = 1e9 + 7;
int dp[maxN][maxM], n, m, k;
vector adj[ maxN ];
void dfs(int u, int p=0) {
for( auto it: adj[u])
if( it != p )
dfs(it, u);
for(int y=1; y<=m; y++) {
dp[u][y] = 1;
for( auto it: adj[u] ) {
if( it != p ) {
int ans = 0;
for(int i=1; i<=m; i++) {
if(abs(i-y) >= k) {
ans += dp[it][i];
if( ans >= mod ) ans -= mod;
}
}
dp[u][y] = 1LL * dp[u][y] * ans % mod;
}
}
}
}
Answer will be \sum_{1 \le i \le M }{DP_{(root, i)}}.
Time Complexity: O(N \times M \times M)
Subtask 2:
Above proposed solution can be optimised to work in O(N \times M).
Let have a look at the recurrence again.
It should be noted that for a given y, there is a continuous range of i where |i-y| \lt K and we can simply subtract the number of ways due to that range from total number of ways by maintaining prefix sum as follows.
const int maxN = 111;
const int maxM = 11111;
const int mod = 1e9 + 7;
int dp[maxN][maxM], n, m, k;
vector adj[ maxN ];
void dfs(int u, int p=0) {
for( auto it: adj[u] ) {
if( it != p ) {
dfs(it, u);
}
}
for(int y=1; y<=m; y++) {
dp[u][y] = 1;
for( auto it: adj[u] ) {
if( it != p ) {
int ans = dp[it][m]; // total sum
int l, r; // finding range to be subtracted
l = max(y - k + 1, 1);
r = min(m, y + k - 1);
if( l <= r ) {
// subtracting range
ans -= dp[it][r] - dp[it][l-1];
if( ans < 0 ) ans += mod;
if( ans > mod ) ans -= mod;
}
dp[u][y] = 1LL * dp[u][y] * ans % mod;
}
}
dp[u][y] += dp[u][y-1]; // maintaining prefix sum
if( dp[u][y] >= mod )
dp[u][y] -= mod;
}
}
Answer will be stored at {DP_{(root, m)}}.
Time Complexity: O(N \times M)
Subtask 3:
This subtask is bit interesting as M \le 10^9. Let just consider following tree consisting of 3 nodes and rooted at node labelled 1 with M = 10 and some K = 2. Note that K = 0 can be handled separately.
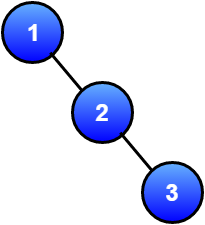
For node 3,
dp_{(3, 1)} = 1
dp_{(3, 2)} = 1
dp_{(3, 3)} = 1
dp_{(3, 4)} = 1
dp_{(3, 5)} = 1
dp_{(3, 6)} = 1
dp_{(3, 7)} = 1
dp_{(3, 8)} = 1
dp_{(3, 9)} = 1
dp_{(3, 10)} = 1
For node 2,
dp_{(2, 1)} = 8
dp_{(2, 2)} = 7
dp_{(2, 3)} = 7
dp_{(2, 4)} = 7
dp_{(2, 5)} = 7
dp_{(2, 6)} = 7
dp_{(2, 7)} = 7
dp_{(2, 8)} = 7
dp_{(2, 9)} = 7
dp_{(2, 10)} = 8
For node 1,
dp_{(1, 1)} = 57
dp_{(1, 2)} = 50
dp_{(1, 3)} = 51
dp_{(1, 4)} = 51
dp_{(1, 5)} = 51
dp_{(1, 6)} = 51
dp_{(1, 7)} = 51
dp_{(1, 8)} = 51
dp_{(1, 9)} = 50
dp_{(1, 10)} = 57
Note that for a leaf node all values are same i.e 1, as we move a level up atmost first K-1 and last K-1 values will become variable and remaining values will become constant ( see values from dp_{(2, 2)} to dp_{(2, 9)}). And if we further move a level up atmost first 2 \times (K-1) and last 2 \times (K-1) values will become variable and remaining values will become constant and so on. More Formally, as we move a level up atmost K-1 more values from the front and at most K-1 more values at the back will become variable and rest of the values will become constant. So, why do we need to compute these constant values again and again? Computing it once is enough to solve the given problem.
It should also be noted that in worst case maximum possible height of the tree will be 99 (as N \le 100) and value of K-1 will also be 99 (as K \le 100). It means that in worst case scenario, we may need to find first 99 \times 99 values from front and 99 \times 99 values from back and 1 value for the middle i.e constant value.
How to implement above idea efficiently ?
C++ Code:
// total values needed in wort case
const int L1 = 2 * 99 * 99 + 1;
// total values needed from the front
const int L2 = 99 * 99;
// taking modulo
void add_mod( int &x ) {
if( x < 0 ) x += mod;
if( x >= mod ) x -= mod;
}
int val; // temp variable
void left(int i, int u, int it) {
int cnt, v;
cnt = max(0, i - k);
if( cnt == 0 ) return;
if( cnt <= L2 ) {
val += dp[it][cnt];
} else {
val += dp[it][L2];
add_mod( val );
cnt -= L2;
v = dp[it][L2+1] - dp[it][L2];
add_mod( v );
if( cnt <= m - 2 * L2) {
val += 1LL * cnt * v % mod;
} else {
val += 1LL * (m - 2 * L2) * v % mod;
add_mod( val );
cnt -= (m - 2 * L2);
val += dp[it][L2+1+cnt] - dp[it][L2+1];
}
}
add_mod( val );
}
void right(int i, int u, int it) {
int cnt, v;
cnt = max(0, m - (i+k) + 1);
if( cnt == 0 ) return;
if( cnt <= L2 ) {
val += dp[it][L1] - dp[it][L1-cnt];
} else {
val += dp[it][L1] - dp[it][L1-L2];
add_mod( val );
cnt -= L2;
v = dp[it][L2+1] - dp[it][L2];
add_mod( v );
if( cnt <= m - 2 * L2 )
val += 1LL * cnt * v % mod;
else {
val += 1LL * (m - 2 * L2) * v % mod;
add_mod( val );
cnt -= (m - 2 * L2);
val += dp[it][L2] - dp[it][L2-cnt];
}
}
add_mod( val );
}
void dfs(int u, int p = 0) {
// i need my children's answer to be
// computed to compute myself
for( auto it: adj[u] )
if( it != p )
dfs( it, u );
int i;
// i denotes the actual value of integer
// to be assigned to node u
for(int j=1; j<=L1; j++) {
dp[u][j] = 1;
if( j > L2+1 ) {
// if we are computing last L2 values
// then i should be updated as follows
i = m - (L1 - j);
} else {
// if we are computing first L2 values
// or the middle constant value
i = j;
}
for( auto it: adj[u] ) {
if( it != p ) {
// resetting variable
val = 0;
// including all the values (say x) to the left of i
// i.e in the range [1, i] that gives (x - i) >= k
left(i, u, it);
// including all the values (say x) to the right of i
// i.e in the range [i, m] that gives (x - i) >= k
right(i, u, it);
// note that for k = 0, x = i is included 2 times. so, we
// need to subtract it once.
if( k == 0 ) {
val -= dp[it][j] - dp[it][j-1];
// adjusting modulo
add_mod( val );
}
dp[u][j] = 1LL * dp[u][j] * val % mod;
}
}
dp[u][j] += dp[u][j-1];
add_mod( dp[u][j] );
}
}
Time Complexity: O(N^2 \times K)
TIME COMPLEXITY:
O(N^2 \times K)
SETTER’S AND TESTER’S SOLUTION:
Setter’s solution can be found [here][132]
Tester’s solution can be found [here][133]
[132]: http://www.codechef.com/download/Solutions/LTIME35/Setter/LABEL.cpp
[133]: http://www.codechef.com/download/Solutions/LTIME35/Tester/LABEL.cpp
 Unfortunately there was a bug in my code during the contest which took me too long , but at least I had the good idea
Unfortunately there was a bug in my code during the contest which took me too long , but at least I had the good idea 