PROBLEM LINKS :
Contest : Division 1
Contest : Division 2
Practice
Setter : Kochekov Kerim
Tester : Istvan Nagy
Editorialist : Anand Jaisingh
DIFFICULTY
Medium
PREREQUISITES :
Sylvester’s Criterion, Basic Arithmetic skills
PROBLEM :
Given 3 integers A,B,C, you need to find the number of positive triplets of integers (a,b,c) , such that 1 \le a \le A , 1 \le b \le B , 1 \le c \le C and for any two real numbers x \ne 0 and y \ne 0 , ax^2+2bxy+cy^2 > x^2 +y^2
QUICK EXPLANATION :
We can re-write the given inequality as (a-1) \cdot x^2 +2bxy +(c-1) \cdot y^2 > 0 . Let P(x,y)=(a-1) \cdot x^2 +2bxy +(c-1) \cdot y^2. We can re-write P(x,y) as 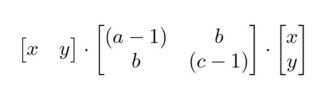
Now, P(x,y) > 0 \forall x \ne 0 , y \ne 0 if the matrix in the middle is Positive definite , after which we use Sylvester’s Criterion for Positive Definiteness of a matrix and some ad-hoc logic to find possible values of (a,b,c).
EXPLANATION :
The first thing that comes to mind is that we can rearrange the given inequality a little bit. We can :
ax^2+2bxy+cy^2 > x^2 +y^2
ax^2 - x^2 +2bxy +cy^2 -y^2 > 0
x^2(a-1) + 2bxy + y^2(c-1) >0
(a-1)\cdot x^2 + 2bxy +(c-1) \cdot y^2 > 0
Now, let P(x,y)= (a-1) \cdot x^2 + 2bxy + (c-1) \cdot y^2
Note that P(x,y) is a polynomial in two variables (x,y)
We can rewrite using a matrix equation as :
P(x,y) =
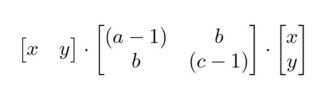
For this polynomial P(x,y) to be > 0 for all x \ne 0 and y \ne 0 , we need the matrix
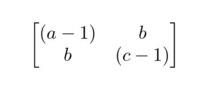
To be Positive Definite. Now, Sylvester’s Criterion says that the given matrix is Positive Definite, if all its Principal Minor’s ( A Principal Minor is the determinant of some top left k \cdot k matrix ) are positive.
This gives us two equations to solve :
(1) (a-1) > 0, \hspace{0.2cm} a > 1
(2) (a-1) \cdot (c-1) - b^2 > 0 , \hspace{0.2cm} (a-1) \cdot (c-1) > b^2
Now, we’ve reduced our original problem to the following :
For each b in the range [1,B] we need to find the number of pairs of integers (a,c), 1 \le a \le A , 1 \le c \le C and (a-1) \cdot (c-1) > b^2 . Since B is rather small, we can simulate this process.
Let’s see how we can do this for a fixed integer b.
An important observation we can make is that if both (a-1) and (c-1) are > b , then the product (a-1) \cdot (c-1) is > b^2 , and if (a-1) and (c-1) < b then (a-1) \cdot (c-1) < b^2
So we are left with 3 cases to consider
Case 1 :
Both (a-1) and (c-1) are > b . In this case, the answer is the number of lattice points inside the rectangle [b+1,A-1] \times [b+1,C-1]
Case 2 :
Here we consider the case when a-1 \le b . For some (a-1) \le min(b,A-1) , the minimum number it needs to be multiplied by is \left\lfloor\frac{b^2}{a-1}\right\rfloor +1 . So we iterate over each possible a in the range [2,min(b,A-1)] and find the number of corresponding possible (c-1)'s
Case 3 :
And, analogous to Case 2, we do similarly when (c-1) \le min(b,C-1).
In the end, just don’t forget to take the final answer Modulo 10^9+7.
That’s it, thank you !
Your Comment’s are Welcome !
I also suggest that you read another wonderful approach by pick_pacemen in the comments section
COMPLEXITY ANALYSIS :
Time Complexity : O( T \cdot B^2 )
Space Complexity : O(1)
SOLUTION LINKS :
Setter
#include "bits/stdc++.h"
#define MOD 1000000007
#define debug(x) cerr<< #x <<" = "<< x<<endl;
using namespace std;
int f(int x,int y){return int((x*1.0*x)/y);}
int mod(long long x){return (x%MOD);}
int main(){
int t;
scanf("%d",&t);
while(t--){
int a,b,c,ans=0;
scanf("%d%d%d",&a,&b,&c);
//(a-1)(c-1)>b*b and a>1
for(int i=1;i<=b;i++){
ans=mod(max(0,c-i-1)*1LL*max(0,a-i-1)+ans);//1<=b+1<a,c
for(int j=2;j<=min(a,i+1);j++)//2<=a<=b+1<c
ans=mod(ans+max(0,c-f(i,j-1)-1));
for(int j=2;j<=min(c,i+1);j++)//1<=c<=b+1<a
ans=mod(ans+max(0,a-f(i,j-1)-1));
}
printf("%d\n",ans);
}
return 0;
}
Tester
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T &a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if (g == endd) {
assert(cnt > 0);
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
//assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
int solver(int A, int B, int C)
{//A<=C
int res = 0, mod = 1e9 + 7;
for (int b = 1; b <= B; ++b)
{//b*b < a*c
int bb = b * b;
//if a < c && a <= b
for (int a = 1; a <= min(A, b); ++a)
{
int minc = (bb + a - 1) / a;
while (minc * a <= bb)
++minc;
if (minc <= C)
{
res = res + C - minc + 1;
if (res > mod)
res -= mod;
}
}
//if c < a && c <= b
for (int c = 1; c <= min(C, b); ++c)
{
int mina = (bb + c - 1) / c;
while (mina * c <= bb)
++mina;
if (mina <= A)
{
res = res + A - mina + 1;
if (res > mod)
res -= mod;
}
}
//if a > b && c > b
if (A > b)
{
res = (res + static_cast<int64_t>(A - b)*(C - b)) % mod;
}
}
return res;
}
int main(int argc, char** argv)
{
#ifdef HOME
if (IsDebuggerPresent())
{
freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
int T, A, B, C;
//T=readIntLn(1, 10);
scanf("%d", &T);
for (int tc = 0; tc < T; ++tc)
{
//A = readIntSp(1, 1000000000);
//B = readIntSp(1, 5000);
//C = readIntLn(1, 1000000000);
scanf("%d %d %d", &A, &B, &C);
int sol = solver(min(A, C) - 1, B, max(A, C) - 1);
printf("%d\n", sol);
}
//assert(getchar() == -1);
return 0;
}
Editorialist
//#pragma GCC optimize("Ofast,no-stack-protector")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx")
//#pragma GCC target("avx,tune=native")
// Anand Jaisingh
#include<bits/stdc++.h>
using namespace std;
typedef complex<double> base;
typedef long double ld;
typedef long long ll;
#define pb push_back
#define pii pair<int,int>
#define pll pair< ll , ll >
#define vi vector<int>
#define vvi vector< vi >
const int maxn=(int)(2e5+5);
const ll mod=(ll)(1e9+7);
int a[maxn];
int mul(ll a,ll b)
{
return (a*b)%mod;
}
int add(int a,int b)
{
int ret=a+b;
if(ret>=mod)
{
ret-=mod;
}
return ret;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);
int t;cin>>t;
while(t>0)
{
int A,B,C,res=0;
cin>>A>>B>>C;
for(int b=1;b<=B;b++)
{
int sq=b*b;
int r1=max(0,A-1-(b+1)+1),r2=max(0,C-1-(b+1)+1),prod=mul(r1,r2);
res=add(res,prod);
for(int k1=1;k1<=min(b,A-1);k1++)
{
int other=(sq/k1)+1;
int sz=max(0,C-1-other+1);
res=add(res,sz);
}
for(int z=1;z<=min(b,C-1);z++)
{
int other=(sq/z)+1;
int sz=max(0,A-1-other+1);
res=add(res,sz);
}
}
cout<<res<<endl;t--;
}
return 0;
}