LARSQR31-Editorial

[devendra7700]

PROBLEM LINK:

Contest Division 1
Contest Division 2
Contest Division 3
Contest Division 4

Setter: Aditya Mittal
Tester: Satyam, Jatin Garg
Editorialist: Devendra Singh

DIFFICULTY:

2179

PREREQUISITES:

Binary Search, Sparse Table

PROBLEM:

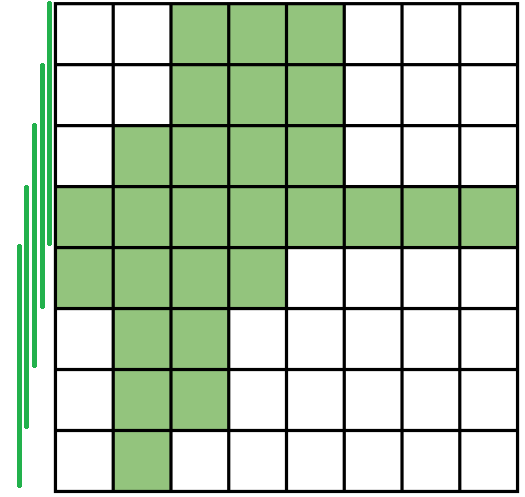
Chef has a garden of size N \times N. The garden is divided into N^2 squares of size 1\times 1 each.

Chef has plants in some unit squares of the garden, because of which, that part looks green.
Formally, for the i^{th} row (0 \le i \lt N), Chef has plants in all the columns from A_i to B_i (both inclusive) where 0 \le A_i \le B_i \lt N.

Help Chef find the length of the side of the largest square that is green.

EXPLANATION:

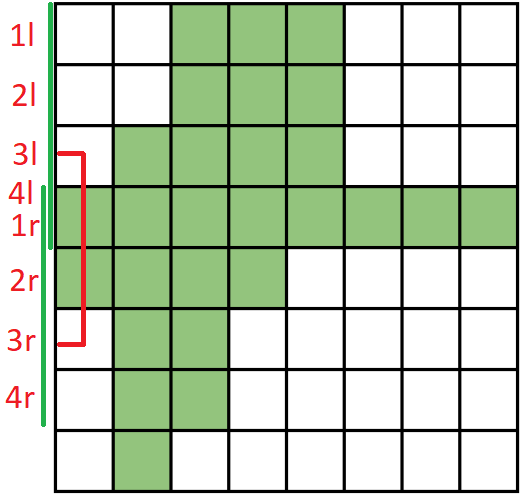
Observation : If there exists a square of side length L that is green, then there exists a square of side length L-1 that is green too. To prove this, just cut the square of side L-1 from the square of side length L (that is green) from the top left corner of it.
This observation suggests that length of the largest square that is green is binary searchable.

We can binary search over the length of the square and for a particular length check if there exists some square with that length which is green. If there exists some square of length L that is green then for some L consecutive rows the intersection of columns that are green must be \geq L. For a particular length L iterate over all the rows from i = 0 to N-1-L and check whether the intersection of green columns for the next L consecutive rows (starting from i^{th} row) is \geq L.

Intersection of two column ranges is calculated as

Let p1 and p2 be two column ranges that are green.(p1.F=L and p1.S=R)

pair<int,int> get(pair<int,int> p1, pair<int,int> p2)
{
    if (p1.F > p2.F)
        swap(p1, p2);
    if (p2.F > p1.S)
        return {1, 0};// To make length of intersection as 0
    return {p2.F, min(p1.S, p2.S)};
}

Segment tree is not used here to get the intersection as it answers a query in O(log(N)) time , where N is the size of the array, which would result in O(Nlog^2(N)) time complexity which is not fast enough to pass the test cases.

We need an efficient way to get the intersection of green columns for L consecutive rows. Sparse table can provide the length of the intersection in O(1) time with O(Nlog(N)) precomputation. Some other data structure like sqrt-tree will also serve the same purpose. Thus we can binary search over the length of side of largest green square and each time the check function inside binary seach algorithm can be implemented in O(N) time. Overall the time complexity of the solution including pre-computation is O(Nlog(N)).

For details of implementation please refer to the attached solutions.

TIME COMPLEXITY:

O(Nlog(N)) for each test case.

SOLUTION:

Setter's solution

#include<bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/detail/standard_policies.hpp>
using namespace std;
using namespace __gnu_pbds;
#define ll long long
#define int long long
#define endl "\n"
#define fi first
#define se second
#define fastio ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define fr(a,b,c) for(int a=b; a<c; a++)
#define frr(a,b,c) for(int a=b;a>=c;a--)
#define pb push_back
#define pii pair<int,int>
#define R(a) ll a; cin >> a;
#define RS(a) string  a; cin >> a;
typedef tree<long long,null_type,greater<long long>,rb_tree_tag,tree_order_statistics_node_update> ordered_set;
typedef tree<long long,null_type,less<long long>,rb_tree_tag,tree_order_statistics_node_update> ordered_set1;
#define RA(a, n) ll a[(n) + 1] = {}; fr(i, 1, (n)+1) {cin >> a[i];}
#define RM(a, n, m) int a[n + 1][m + 1] = {}; fr(i, 1, n+1) {fr(j, 1, m+1) cin >> a[i][j];}
#define reset(X) memset(X, 0, sizeof(X))
using vi=vector<int>;
const int inf = 1e18;
const int mod=998244353;
void __print(long x) {cerr << x;}
void __print(long long x) {cerr << x;}
void __print(unsigned x) {cerr << x;}
void __print(unsigned long x) {cerr << x;}
void __print(unsigned long long x) {cerr << x;}
void __print(float x) {cerr << x;}
void __print(double x) {cerr << x;}
void __print(long double x) {cerr << x;}
void __print(char x) {cerr << '\'' << x << '\'';}
void __print(const char *x) {cerr << '\"' << x << '\"';}
void __print(const string &x) {cerr << '\"' << x << '\"';}
void __print(bool x) {cerr << (x ? "true" : "false");}

template<typename T, typename V>
void __print(const pair<T, V> &x) {cerr << '{'; __print(x.first); cerr << ','; __print(x.second); cerr << '}';}
template<typename T>
void __print(const T &x) {int f = 0; cerr << '{'; for (auto &i: x) cerr << (f++ ? "," : ""), __print(i); cerr << "}";}
void _print() {cerr << "]"<<endl;}
template <typename T, typename... V>
void _print(T t, V... v) {__print(t); if (sizeof...(v)) cerr << ", "; _print(v...);}
#ifndef ONLINE_JUDGE
#define deb(x...) cerr << "[" << #x << "] = ["; _print(x)
#else
#define deb(x...)
#endif
#define all(x) (x).begin(),(x).end()
unsigned int power(int x, unsigned int y, int p)
{
    int res = 1;
    x = x % p;
    while (y > 0)
    {
        if (y & 1)
            res = (res*x) % p;
        y = y>>1;
        x = (x*x) % p;
    }
    return res;
}
int modInverse(int n, int p)
{
    return power(n, p-2, p);
}
const int maxn=1e6+5;
int t[4*maxn][2];
bool f;
void build(int a[], int v, int tl, int tr) {
    if (tl == tr) {
        if(!f)
        t[v][0] = a[tl];
        else
            t[v][1]=a[tl];
    } else {
        int tm = (tl + tr) / 2;
        build(a, v*2, tl, tm);
        build(a, v*2+1, tm+1, tr);
        if(!f)
        {
            t[v][0]= max(t[v*2][0], t[v*2+1][0]);
        }
        else
        t[v][1] = min(t[v*2][1], t[v*2+1][1]);
    }
}
int sum(int v, int tl, int tr, int l, int r) {
    if (l > r)
    {
        if(!f)
        {
            return 0;

        }
        else
        {
            return inf;
        }
    }

    if (l == tl && r == tr) {
        if(f==0)
        return t[v][0];
        else
            return t[v][1];
    }
    int tm = (tl + tr) / 2;
    if(f==0)
    return max(sum(v*2, tl, tm, l, min(r, tm)), sum(v*2+1, tm+1, tr, max(l, tm+1), r));
           else
            return min(sum(v*2, tl, tm, l, min(r, tm)), sum(v*2+1, tm+1, tr, max(l, tm+1), r));
}
signed main()
{
    fastio;
    int t=1;
    //cin>>t;
    while(t--)
    {
       int n;
       cin>>n;
      vector<pair<int,int>>v;
      int a[n],b[n];
      fr(i,0,n)
      {
          cin>>a[i]>>b[i];
      }
      build(a,1,0,n-1);
      f=1;
      build(b,1,0,n-1);
      f=0;
      int cur=0;
      int ans=1;
      fr(i,0,n)
      {
          int x1 = sum(1,0,n-1,cur,i);
          f=1;
          int x2 = sum(1,0,n-1,cur,i);
          f=0;
          int xx = x2-x1+1;
          int yy = i-cur+1;
         // cout<<x1<<" "<<x2<<endl;
          if(xx<=0)cur=i;
          else
          {
              ans  = max(ans, min(i-cur+1,xx));
              if(xx<i-cur+1)
              {
                  cur+=1;
                  i-=1;
              }
              else
              {
                  continue;
              }
          }
      }
      cout<<ans<<endl;
    }
}

Tester-1's Solution

#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast,unroll-loops")
#include <bits/stdc++.h>
using namespace std;
#ifndef ONLINE_JUDGE    
#define debug(x) cerr<<#x<<" "; _print(x); cerr<<nline;
#else
#define debug(x);  
#endif 
#define ll long long 
 
 
/*
------------------------Input Checker----------------------------------
*/
 
long long readInt(long long l,long long r,char endd){
    long long x=0;
    int cnt=0;
    int fi=-1;
    bool is_neg=false;
    while(true){   
        char g=getchar();
        if(g=='-'){  
            assert(fi==-1);     
            is_neg=true;
            continue;
        }
        if('0'<=g && g<='9'){
            x*=10;
            x+=g-'0';
            if(cnt==0){
                fi=g-'0';
            }
            cnt++;
            assert(fi!=0 || cnt==1);
            assert(fi!=0 || is_neg==false);
 
            assert(!(cnt>19 || ( cnt==19 && fi>1) ));
        } else if(g==endd){
            if(is_neg){
                x= -x;
            }
 
            if(!(l <= x && x <= r))
            {
                cerr << l << ' ' << r << ' ' << x << '\n';
                assert(1 == 0);
            }
 
            return x;
        } else {
            assert(false);
        }
    }
}
string readString(int l,int r,char endd){
    string ret="";
    int cnt=0;
    while(true){
        char g=getchar();
        assert(g!=-1);
        if(g==endd){
            break;
        }
        cnt++;
        ret+=g;
    }
    assert(l<=cnt && cnt<=r);
    return ret;
}
long long readIntSp(long long l,long long r){
    return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
    return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
    return readString(l,r,'\n');
}
string readStringSp(int l,int r){
    return readString(l,r,' ');
}
 
 
/*
------------------------Main code starts here----------------------------------
*/
const ll MOD=1e9+7;
vector<ll> readv(ll n,ll l,ll r){
    vector<ll> a;
    ll x;
    for(ll i=1;i<n;i++){  
        x=readIntSp(l,r);  
        a.push_back(x);   
    }
    x=readIntLn(l,r);
    a.push_back(x);
    return a;  
}
const ll MAX=3000300;
void solve(){  
    ll n=readIntLn(1,1e6);
    vector<ll> a(n+5),b(n+5);
    for(ll i=1;i<=n;i++){
        a[i]=readIntSp(0,n-1);
        b[i]=readIntLn(a[i],n-1); 
    }
    ll ans=0,l=0; 
    multiset<ll> lft,rght;      
    lft.insert(n+1); rght.insert(-1);
    a[0]=n+1,b[0]=-1; 
    for(ll i=1;i<=n;i++){
        lft.insert(a[i]); rght.insert(b[i]);
        while(1){
            auto il=*(--lft.end()),ir=*(rght.begin()); 
            if(ir-il+1<i-l+1){
                lft.erase(lft.find(a[l])); rght.erase(rght.find(b[l]));
                l++;
            }
            else{
                break;
            }
        }
        ans=max(ans,i-l+1); 
    }
    cout<<ans;
    return;  
}
int main(){
    ios_base::sync_with_stdio(false);                         
    cin.tie(NULL);                              
    #ifndef ONLINE_JUDGE                 
    freopen("input.txt", "r", stdin);                                                
    freopen("output.txt", "w", stdout);  
    freopen("error.txt", "w", stderr);                          
    #endif         
    ll test_cases=1 ;//readIntLn(1,100); 
    while(test_cases--){
        solve();
    }
    assert(getchar()==-1);
    return 0;
}

Tester-2's Solution

// Jai Shree Ram  
  
#include<bits/stdc++.h>
using namespace std;

#define rep(i,a,n)     for(int i=a;i<n;i++)
#define ll             long long
#define int            long long
#define pb             push_back
#define all(v)         v.begin(),v.end()
#define endl           "\n"
#define x              first
#define y              second
#define gcd(a,b)       __gcd(a,b)
#define mem1(a)        memset(a,-1,sizeof(a))
#define mem0(a)        memset(a,0,sizeof(a))
#define sz(a)          (int)a.size()
#define pii            pair<int,int>
#define hell           1000000007
#define elasped_time   1.0 * clock() / CLOCKS_PER_SEC



template<typename T1,typename T2>istream& operator>>(istream& in,pair<T1,T2> &a){in>>a.x>>a.y;return in;}
template<typename T1,typename T2>ostream& operator<<(ostream& out,pair<T1,T2> a){out<<a.x<<" "<<a.y;return out;}
template<typename T,typename T1>T maxs(T &a,T1 b){if(b>a)a=b;return a;}
template<typename T,typename T1>T mins(T &a,T1 b){if(b<a)a=b;return a;}

// -------------------- Input Checker Start --------------------
 
long long readInt(long long l, long long r, char endd)
{
    long long x = 0;
    int cnt = 0, fi = -1;
    bool is_neg = false;
    while(true)
    {
        char g = getchar();
        if(g == '-')
        {
            assert(fi == -1);
            is_neg = true;
            continue;
        }
        if('0' <= g && g <= '9')
        {
            x *= 10;
            x += g - '0';
            if(cnt == 0)
                fi = g - '0';
            cnt++;
            assert(fi != 0 || cnt == 1);
            assert(fi != 0 || is_neg == false);
            assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
        }
        else if(g == endd)
        {
            if(is_neg)
                x = -x;
            if(!(l <= x && x <= r))
            {
                cerr << l << ' ' << r << ' ' << x << '\n';
                assert(false);
            }
            return x;
        }
        else
        {
            assert(false);
        }
    }
}
 
string readString(int l, int r, char endd)
{
    string ret = "";
    int cnt = 0;
    while(true)
    {
        char g = getchar();
        assert(g != -1);
        if(g == endd)
            break;
        cnt++;
        ret += g;
    }
    assert(l <= cnt && cnt <= r);
    return ret;
}
 
long long readIntSp(long long l, long long r) { return readInt(l, r, ' '); }
long long readIntLn(long long l, long long r) { return readInt(l, r, '\n'); }
string readStringLn(int l, int r) { return readString(l, r, '\n'); }
string readStringSp(int l, int r) { return readString(l, r, ' '); }
void readEOF() { assert(getchar() == EOF); }
 
vector<int> readVectorInt(int n, long long l, long long r)
{
    vector<int> a(n);
    for(int i = 0; i < n - 1; i++)
        a[i] = readIntSp(l, r);
    a[n - 1] = readIntLn(l, r);
    return a;
}
 
// -------------------- Input Checker End --------------------


int solve(){
 		int n = readIntLn(1,1e6);
 		vector<pii>segs;
 		for(int i = 0; i < n; i++){
 			int x = readIntSp(0,n - 1);
 			int y = readIntLn(x,n - 1);
 			segs.push_back({x,y});
 		}
 		vector<vector<int>> mx(22,vector<int>(n + 1));
 		auto mn = mx;
 		vector<int> LOG(n + 1);
 		for(int i = 0; i < n; i++){
 			mx[0][i] = segs[i].x;
 			mn[0][i] = segs[i].y;
 		}
 		for(int i = 2; i <= n; i++){
 			LOG[i] = 1 + LOG[i/2];
 		}
 		for(int x = 1; x <= 21; x++){
 			for(int i = 0; i + (1 << (x - 1)) < n; i++){
 				mx[x][i] = max(mx[x - 1][i],mx[x - 1][i + (1 << (x - 1))]);
 				mn[x][i] = min(mn[x - 1][i],mn[x - 1][i + (1 << (x - 1))]);
 			}
 		}
 		auto query = [&](int l,int r){
 			int j = LOG[r - l + 1];
 			int mxx = max(mx[j][l],mx[j][r - (1 << j) + 1]);
 			int mnn = min(mn[j][l],mn[j][r - (1 << j) + 1]);
 			return mnn - mxx + 1;
 		};
 		int ans = 1;
 		for(int i = 0; i < n; i++){
 			int mxL = segs[i].x;
 			int mnR = segs[i].y;
 			int R = i;
 			int L = 0;
 			while(L <= R){
 				int M = (L + R)/2;
 				int val = query(M,i);
 				if(val >= i - M + 1){
 					ans = max(ans,i - M + 1);
 					R = M - 1;
 				}else{
 					L = M + 1;
 				}
 			}
 			
 		}
 		cout << ans << endl;
 return 0;
}
signed main(){
    ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    //freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    #ifdef SIEVE
    sieve();
    #endif
    #ifdef NCR
    init();
    #endif
    int t=1;//cin>>t;
    while(t--){
        solve();
    }
    return 0;
}
 

This text will be hidden

Editorialist's Solution

#include "bits/stdc++.h"
using namespace std;
#define ll long long
#define pb push_back
#define all(_obj) _obj.begin(), _obj.end()
#define F first
#define S second
#define pll pair<ll, ll>
#define vll vector<ll>
ll INF = 1e18;
const int N = 1e6 + 11, mod = 1e9 + 7;
ll max(ll a, ll b) { return ((a > b) ? a : b); }
ll min(ll a, ll b) { return ((a > b) ? b : a); }
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
pll st[N][26];
int lg[N + 1];
pll get(pll p1, pll p2)
{
    if (p1.F > p2.F)
        swap(p1, p2);
    if (p2.F > p1.S)
        return {1, 0};
    return {p2.F, min(p1.S, p2.S)};
}
int int_len(int L, int R)
{
    int j = lg[R - L + 1];
    pll p = get(st[L][j], st[R - (1 << j) + 1][j]);
    return p.S - p.F + 1;
}
void sol(void)
{
    int n;
    cin >> n;
    vector<pll> vp(n);
    for (int i = 0; i < n; i++)
        cin >> vp[i].F >> vp[i].S;
    for (int i = 0; i < n; i++)
        st[i][0] = vp[i];
    for (int j = 1; j <= 25; j++)
        for (int i = 0; i + (1 << j) <= n; i++)
            st[i][j] = get(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
    lg[1] = 0;
    for (int i = 2; i <= N; i++)
        lg[i] = lg[i / 2] + 1;
    int l = 1, r = n, mid;
    while (l <= r)
    {
        mid = (l + r) / 2;
        bool istrue = false;
        for (int i = 0; i <= n - mid; i++)
        {
            if (int_len(i, i + mid - 1) >= mid)
                istrue = true;
        }
        if (istrue)
            l = mid + 1;
        else
            r = mid - 1;
    }
    cout << r;
    return;
}
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL), cout.tie(NULL);
    int test = 1;
    // cin>>test;
    while (test--)
        sol();
}

[kiss_my_axe_2]

Time limit for this problem is given 1 - 1.5 secs, what does this mean, is it range or something.
Also for (segment tree) O(Nlog^2(N)) solution to pass what should be the time limit or constrains.

[a3000]

why does dp solution not work here?

[david_s]

I tried a more direct approach. As we work down the rows, maintain a list (variable length array) of those rows above which may contribute to a larger green square than we have so far. If the current row is narrower than any of the stored rows above at either start or end, reduce the length of the row above. Do not keep rows which are the same length as those above.

This method passed 8 out of the 14 test cases. I have no idea why it failed in other cases. You can see my solution at CodeChef: Practical coding for everyone If anyone has any idea why is failed for some cases I would like to know.

[termii]

dp solution does work, I used one. PREREQUISITES: binary search, dp, two pointer

To be more specific, I binary search for the correct solution.

public static void solve() throws IOException {
    //read input
    int n = sc.nextInt();
    Interval[] arr = new Interval[n];
    for (int i = 0; i < n; i++) arr[i] = new Interval(sc.nextInt(), sc.nextInt());

    //binary search
    int L = 1; //always possible (at least 1x1)
    int R = n+1; //never possible

    while(L + 1 < R){
        int M = L + (R-L)/2;
        if(isPossible(M, n, arr)) L = M;
        else R = M;
    }

    //print solution
    out.println(L);
}

Note that I am using a small Interval class that can return its own size and combine itself with another Interval to make a new one:

static class Interval {
    public long left;
    public long right;
    public Interval(long left, long right) {
        this.left = left;
        this.right = right;
    }

    //returns the size of the interval
    public long getIntervalSize(){
        if(left == -1 || right == -1 || left > right) return 0;
        else return (right-left+1);
    }

    //returns the overlapping interval
    public Interval generateOverlap(Interval other){
        long start = max(left, other.left);
        long end = min(right, other.right);

        if(start > end) return new Interval(-1,-1);
        return new Interval(start, end);
    }

    @Override
    public String toString() { return "(" + left + ", " + right + ")"; }
}

dp-part, an example - Testcase 2 of the problem statement, lets check if a square of size 4x4 exists:

I have marked on the left side the different squares that could exists and from where to where they reach. [1, 4], [2, 5], [3, 6], [4, 7] and [5, 8] namely. The easy and slow solution would be to check if there is a square in either of these intervals. O(n²).
With dp we can change the problem statement a little bit though. We don’t ask if there is a square that starts with line 1 and ends with 4 or starts at i and ends at i+3. We ask if, for a line i, there exists a square that contains that line.

Here I marked what I mean. Lets say we want to know if i=4 lies within a 4x4 square. we know that it lies in the intervals [1,4], [4,7] and anything inbetween. We can generate 2 dp arrays that keep track how the intervals above and below look. In this case we would have 2 dp arrays storing:
aboveDP: [interval(4), interval(3,4), interval(2,4), interval(1,4)]
belowDP: [interval(4), interval(4,5), interval(4,6), interval(4,7)]
Note 2 things.
First, we had to generate and store 4*2 intervals. This takes O(n) because each interval can be generated in constant time. [1,4] = [2,4] + [1].
Second, having these 2 dp array allows us to check if, for example, [3, 6] = [3,4] + [4,6] is a valid square in constant time O(1).

Here is the code:

//O(n)
public static boolean isPossible(int M, int n, Interval[] arr){
    //split the grid in parts of height M
    for (int i = M-1; i < n; i += M) {
        Interval[] intervalsAbove = new Interval[M];
        Interval[] intervalsBelow = new Interval[M];

        intervalsAbove[0] = arr[i];
        for (int j = 1; j < M; j++) {
            if(i-j < 0) intervalsAbove[j] = new Interval(-1,-1);
            else intervalsAbove[j] = (intervalsAbove[j-1]).generateOverlap(arr[i-j]);
        }

        intervalsBelow[0] = arr[i];
        for (int j = 1; j < M; j++) {
            if(i+j >= n) intervalsBelow[j] = new Interval(-1,-1);
            else intervalsBelow[j] = intervalsBelow[j-1].generateOverlap(arr[i+j]);
        }

        //sliding window
        for (int j = 0; j < M; j++) if((intervalsBelow[j].generateOverlap(intervalsAbove[M-1-j]).getIntervalSize()) >= M) return true;
    }
    return false;
}

full solution: CodeChef: Practical coding for everyone

[aging1986]

I used segment tree to solve this problem.
First, define f(i, j) as the number of consecutive green grids above grid (i, j). For row i, if the green range is [A_i, B_i], we have below formula:
f(i, j) = 1 + f(i - 1, j) when j \in [A_i, B_i], otherwise f(i, j) = 0.
We can further find out that, for each row i, the value f(i, j) first non-decrease, then non-increase. That’s due to the fact that green grids of each row is consecutive.
As the problem requests to find largest square, we can check from 1 to N if that square exists for each row. The maximum checking time is 2N.
For each sqare side length K, we can binary search on segment tree which holds f(i, j). Just first the left and right boundary of K, then check if the distance between them is larger than or equal to K.
Update of segment tree: set [1, A_i - 1] and [B_i + 1, N] to 0, and increase [A_i, B_i] by 1.
The overall time complexity is O(NlogN).

[lengli]

In fact, I passed this problem using the line segment tree, (maybe the data is not strong enough?), here is my passing code.

/*
lengli_QAQ
Hope there are no bugs!!!
*/
#include <bits/stdc++.h>
#define fastio ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define endl '\n'
#define getcha() (S==T&&(T=(S=fsr)+fread(fsr,1,1<<15,stdin),S==T)?EOF:*S++)
char fsr[1<<15],*S=fsr,*T=fsr;
inline int read(){
	int r(0),w(1);char ch;
	while(ch=getcha(),ch>=58 || ch<=47)w=(ch=='-'?-1:1);r=(r<<3)+(r<<1)+ch-48;
	while(ch=getcha(),ch<=57 && ch>=48)r=(r<<3)+(r<<1)+ch-48;
	return r*w;
}
//#define x first
//#define y second

using namespace std;
typedef pair<int,int> PII;
typedef long long LL;

const int N=1000100;

PII a[N];
PII tr[N*2];

inline PII get(PII ll,PII rr)
{
	if(ll.first > rr.first) swap(ll,rr);
	PII res={-1,-1};
	if(rr.first <= ll.second)
	{
		int lll=rr.first;
		int rrr=min(ll.second,rr.second);
		res={lll,rrr};
	}
	return res;
}

int n, m;
void build(){
	for(m=1; m<=n; m<<=1);
	for(int i=m+1; i<=m+n; i++)
		tr[i].first=read(),tr[i].second=read();;
	for(int i=m-1; i; i--)
		tr[i]=get(tr[i<<1],tr[i<<1|1]);
}

inline PII query(int l,int r){
    PII ans={0,1e9};
    for(l=m+l-1,r=m+r+1;l ^ r ^ 1;l>>=1,r>>=1){
        if(~l&1)ans=get(tr[l ^ 1],ans);
        if(r&1)ans=get(tr[r ^ 1],ans);
    }
    return ans;
}


inline bool check(int x)
{
	for(int i=1;i<=n-x+1;i++)
	{
		int a=i,b=i+x-1;
		PII t=query(a,b);
		int l=t.first,r=t.second;
		if(l==-1) continue;
		
		if(r-l+1 >=x ) return 1;
	}
	return 0;
}


signed main()
{
    n=read();
    build();
    int l=1,r=n;
    while(l<r)
    {
    	int mid=(l+r+1)/2;
    	if(check(mid)) l=mid;
    	else r=mid-1;
    }
  	
    cout<<l;
    
    return 0;
}

[for_dreams]

space and time complexities are exceeded in most optimal dp way too.

[pavan512]

waant to check my failing edge case

[pavan512]

Hi @devendra7700 , could you please enable Debug mode for this problem as contest is already ended

[giselus]

It can also be solved in linear time using two pointers technique.
Let’s look at intersection on some interval [l,r]. Notice that intervals [l-1,r] and [l,r+1] can’t have larger intersection. Also smaller interval cannot have smaller intersection.
So as normally, let’s have two pointers l,r. If r-l > intersection of (l,r) we want to increase l, as increasing r cannot lead to better answer. It’s similiar in other case.
The last thing is finding intersection after moving one of the pointers. This can be done using minimum/maximum queue.