PROBLEM LINK:
Practice
Division 1
Division 2
Author: Sachin Yadav
Tester: Smit Mandavia
Editorialist: Sachin Yadav
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Ordered-Sets
PROBLEM:
You are given N rectangles of different dimensions and colours. Each of the rectangles has three properties, the colour C_{i}, the length L_{i} and breadth B_{i}. The length L and the breadth B of these rectangles are even and all the rectangles are centred at the origin. The rectangles are placed one over the other. The rectangle i, is obscured by the rectangles j if j > i , that is only the colour of the top rectangle is visible in the overlapping region.
Given the colours and the dimensions of the rectangles, find out how many unit squares of each colour are visible in the final figure.
QUICK EXPLANATION:
As the figure is always symmetric about x and y axis, we need to just calculate the area for a quadrant and then multiply by 4 at the end.
Instead of processing from rectangle 1 to rectangle N, here we go from rectangle N to rectangle 1. So instead of placing the rectangles at top one by one, we place them at the bottom of others.
When we keep on adding rectangles this way, we observe that the outline of the current figure forms a staircase-like structure. So while placing a new rectangle we can find the portion of the rectangle that would be visible once it is placed behind the current figure.
We sum over these visible areas as per the different colours to get the area of each colour in the final figure.
EXPLANATION:
As mentioned above, we would be adding rectangles in reverse from N to 1. At any instant, the outline of the figure forms a staircase structure.
So lets say, at some moment I have placed i rectangles and now I am placing (i+1)^{th} rectangle behind them. Some of the portion of this rectangle will be hidden behind other rectangles and some part visible after placing it. If a portion of the rectangle is visible, then I can say that it will be visible in the final figure as well, as the next rectangles will be placed behind these (i+1) rectangles.
Therefore, for every rectangle, while placing it, I just need to find the area of the part of the rectangle that will be visible after placing it behind the previous rectangles. I add this area to the count of the respective colours for each rectangle and get the final answer.
Now comes the question, how to find the area of the (i+1)^{th} rectangle that is visible in the final figure.
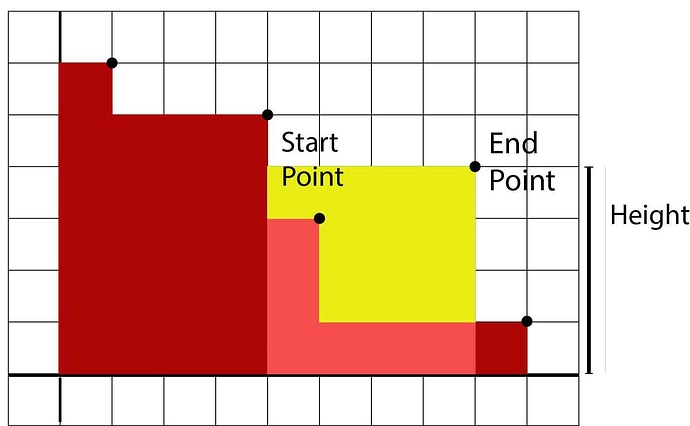
Refer to the figure above.
Now , I am adding a rectangle to this structure, as the structure is forming a staircase-like structure, I can binary search on it to get the starting point a at which the visible portion of this new rectangle starts i.e. a previously added rectangle whose height is just greater or equal to current rectangle’ height in the outline.
Let the length of rectangle be b.
There may be two cases here:
- b \leq a : The rectangle will be completely hidden. It will not contribute to the final figure.
- b > a : Some portion of the rectangle would be visible in the final figure.
Now in the case b > a. We have to consider the contribution of this rectangle in the final figure.
The contribution of this rectangle is
(b-a)\times height - Area of the staircase outline from a to b
Then we update the staircase strucure after inserting this rectangle.
Implementation
For maintaining the staircase structure, I have used an ordered set of pairs with (x,y) coordinates of top-right corner for every rectangle in it.
This structure satisifies the property x_{1}\leq x_{2}\leq x_{3}\leq x_{4}\leq \dots\leq x_{k} and y_{1}\geq y_{2}\geq y_{3}\geq \dots \geq y_{k}.
To add a new rectangle (x,y) beneath these k rectangles, we find the lower_bound of the indices. Now we iterate over the rectangles which lie inside the new rectangle area and remove them one-by-one. As we remove them, we also calculate the area thay had occupied which we subtract from the current rectangles area.
Time Complexity: O(N\times log(N))
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll T, N, C, l, b, c;
struct rect_data{
ll l, h, c;
};
auto ladder_cmp = []( pair<ll,ll> a, pair<ll,ll>b )
{
if(a.second==b.second) return a.first < b.first;
else return a.second > b.second;
};
set<pair<ll,ll> , decltype(ladder_cmp) > rects_set(ladder_cmp);
rect_data rects[100001];
ll clr_cnt[101];
void add_rect(ll i)
{
ll y=rects[i].h, x=rects[i].l, clr=rects[i].c;
if(rects_set.empty()){
clr_cnt[clr]+=x*y;
rects_set.insert({x,y});
return ;
}
auto itr=rects_set.upper_bound(make_pair(x,y));
ll prev_lh=0;
if(itr!=rects_set.begin()) prev_lh=prev(itr)->first;
if(x<=prev_lh) return;
clr_cnt[clr]+=(x-prev_lh)*y;
for( ; itr!=rects_set.end();)
{
if(itr!=rects_set.end() && x<=prev_lh){ clr_cnt[clr]-=x*y; return; }
if(x<=itr->first){ clr_cnt[clr]-=(itr->second)*(x-prev_lh); rects_set.insert({x,y}); return; }
else{
clr_cnt[clr]-=itr->second*(itr->first-prev_lh);
prev_lh=itr->first;
auto iter2=itr++;
rects_set.erase(iter2);
}
}
rects_set.insert({x,y});
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr);
cin>>T;
while(T--)
{
memset(clr_cnt, 0, sizeof(clr_cnt));
rects_set.clear();
cin>>N>>C;
for(ll i=0; i<N; i++)
{
cin>>rects[i].l>>rects[i].h>>rects[i].c;
rects[i].l/=2; rects[i].h/=2;
}
for(ll i=N-1; i>=0; i--)
add_rect(i);
for(ll i=0; i<C; i++)
cout<<4*clr_cnt[i+1]<<" ";
cout<<"\n";
}
return 0;
}
Tester's Solution
#include<bits/stdc++.h>
using namespace std;
#define ll long long int
#define FIO ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define mod 1000000007
int main()
{
FIO;
ll t,n,k,i,j,tmp;
cin >> t;
while(t--){
cin >> n >> k;
ll area[k+1]={0},l[n],b[n],c[n];
set< pair<ll,ll> > s;
set< pair<ll,ll> > :: iterator it;
vector< pair<ll,ll> > vec;
s.insert({0,LLONG_MAX});
s.insert({LLONG_MAX,0});
for(i=0;i<n;i++)
cin >> l[i] >> b[i] >> c[i];
for(i=n-1;i>=0;i--){
tmp=0;
it=s.lower_bound({l[i],LLONG_MIN});
if(it->second<b[i])
vec.push_back({l[i],it->second});
it--;
while(it!=s.begin() && it->first<l[i] && it->second<b[i]){
vec.push_back((*it));
it--;
}
if(it->first<l[i])
vec.push_back({it->first,b[i]});
for(auto x:vec){
it=s.find(x);
if(it!=s.end())
s.erase(it);
}
for(j=0;j<vec.size()-1;j++)
tmp+=(vec[j].first-vec[j+1].first)*(b[i]-vec[j].second);
if(tmp>0)
s.insert({l[i],b[i]});
area[c[i]]+=tmp;
vec.clear();
}
for(i=1;i<=k;i++)
cout << area[i] << " ";
cout << "\n";
}
return 0;
}