PROBLEM LINK
Author: Mann Mehta
Tester: Jaymeet Mehta
Editorialist: Vatsal Parmar
DIFFICULTY
Easy
PREREQUISITES
Basic Math, Triangle Properties, Geometry
PROBLEM
You are given a 9-Queries on an Isosceles Triangle, in which you get to know isosceles sides and any one angle of an Isosceles Triangle. Your task is to predict other two angles of Isosceles Triangle.
EXPLANATION
Here there are total 3-ways such that we select 2 side as an isosceles side in a triangle. That's why total 9-queries are possible for each angel with all 3 ways.(3-Angles × 3-Ways = 9-Queries)
What is Isosceles Triangle ?
In geometry, an isosceles triangle is a triangle that has at least two sides of equal length.
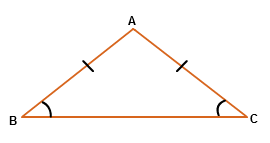
angle ( A ) + angle ( B ) + angle ( C ) = 180
If AB = AC then angle(B) = angle(C)
Now, we go through first three queries Where $AB$ and $AC$ are isosceles side therefore angle(B) = angle(C) .
1) Query-1
Let’s consider angle(A) which is given as A and suppose other two angles angle(B) and angle(C) as X.
Now applying the angle sum property.
angle(A)+angle(B)+angle(C)=180
A + X + X = 180
2X = 180 − A
X = (180 − A) / 2
Let's consider angle ( B ) which is given as B and suppose other two angles angle(A) as X and angle(C) as Y.
Now applying the angle sum property.
angle(A)+angle(B)+angle(C)=180
X + B + Y = 180
We know that angle(B) = angle(C) therefore angle(C)=B
X + B + B = 180
X + 2B = 180
X = 180 − 2B
Now in this query angle ( B ) and angle ( C ) is an isosceles angle’s therefore to make a valid triangle it’s value must be in range :- 0 < angle ( B ), angle ( C ) < 90
3) Query-3
Let’s consider angle ( C ) which is given as C and suppose other two angles angle ( A ) as X and angle(B) as Y.
Now applying the angle sum property.
angle(A)+angle(B)+angle(C)=180
X + Y + C + = 180
We know that angle(B) = angle(C) therefore angle(B)=C
X + C + C + = 180
X + 2C = 180
X = 180 − 2C
Now in this query angle ( B ) and angle ( C ) is an isosceles angle’s therefore to make a valid triangle it’s value must be in range :- 0 < angle ( B ),angle ( C ) < 90
Now similarly go for other queries also.