Whats ur logic for both the problems
int term1= max(row-1-x,x);
int term2 = max(column-1-y,y);
cout << term1 +term2 << endl;
first one
Second one was max(term1,term2)
logic not the code 
Why
maximum manhattan distance from the corners will be the answer
For the first one the answer is maximum manhattan distance to corners
max({abs(0-x)+abs(0-y), abs(r-1-x)+abs(0-y), abs(0-x)+abs(c-1-y), abs(r-1-x)+abs(c-1-y)})
For second one it is the maximum distance from walls, because the 4 corners can be reached within the maximum of these distances
max({abs(r-1-x), abs(x), abs(c-1-y), abs(y)})
I’m sure if you’ll draw some examples, you’ll see It.
In the first case, the farthest point will be one of the corners. So you need to find the furthest corner.
In the second case you increase your size in all directions so it’s like making your box bigger until it touches all the sides of the main grid. As in each move you get one more unit closer to each side, the answer would be the maximum distance from each side.
https://www.codechef.com/viewsolution/32456434
above link is for Apocalypse revisited can you point out what’s wrong…
#include <iostream>
using namespace std;
int main() {
int t;
cin>>t;
while(t–)
{
int r,c; cin>>r>>c;
int x,y; cin>>x>>y;
r-=1; c-=1;
//cout<<x<< " "<<c-x<<endl;
//cout<< y<< " "<<r-y<<endl;
int res=max(x,r-x);
int res2=max(c-y,y);
cout<<res+res2<<endl;
}
return 0;
}
above is code for Apocalypse … can you point out the flaw.
Thank U in advance
u did
res=max(x,y);
instead of
res=max(x,r-x);
in endgame and similar for res2 rest seems right.
The logic is that the maximum time that the virus will take to spread will be to one of the corner vertices based on Manhattan Distance.
For First question:
Since diagonal movement is not allowed, hence we need to find the maximum distance to one of the corners with the following logic:
int option1 = (r - x - 1) + (c - y - 1); // For corner labelled 16
int option2 = (r - 1 - x) + y; // For corner labelled 13
int option3 = x + y; // For corner labelled 1
int option4 = x + (c - 1 - y); // For corner labelled 4
int answer = max(max(option1, option2), max(option3, option4));
For Second Question:
Since, diagonal movement is allowed in this one, we can take the same amount of time to reach the corners as we would take to reach the top, bottom, left or right or the current column and row we are situated in.
int option1 = c - 1 - y; // For bottom end of the column
int option2 = y; // For top end of the column
int option3 = x; // For left end of the row
int option4 = r - x - 1; // For right end of the row
int answer = max(max(option1, option2), max(option3, option4));
Hope it helps!
Thanks!
does this competition rated ??
I dont understand this part “same amount of time to reach the corners as we would take to reach the top,bottom …”
Replying to @vai53
Okay so consider the example when you are initially located at block 15. Our task is to find the time we take to reach the farthest point on the grid with all typed of movements allowed.
Our initial position looks like this. At each day, we just make the moves which take us towards any corner point i.e 1, 4, 13 or 16.
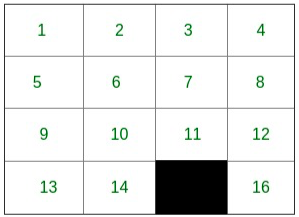
Path for corner 1:
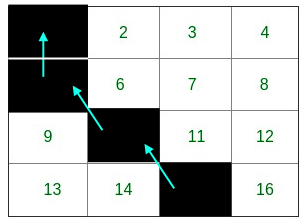
Time Taken: 3 days
Path for corner 4:
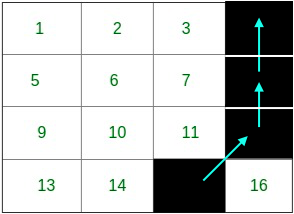
Time Taken: 3 days
Path for corner 13:
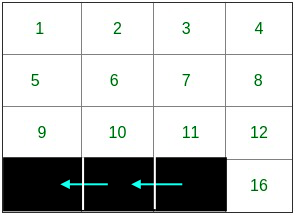
Time Taken: 2 days
Path for corner 16:
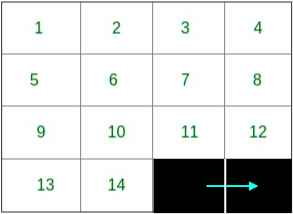
Time Taken: 1 day
Now, we notice that the time taken to reach the farthest corner is 3 days. But if you observe carefully then this is also the time taken to reach the farthest point in the initial row or column.
The farthest point in the initial row or column in our situation is 3.
Path for cell 3:
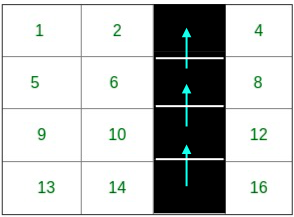
Time Taken: 3 days
Thus, we observe that it is possible to reach any corner within the time taken to reach the farthest point in the initial row or column. This can be deduced through some observations and also dry running some examples to get a better picture.