Problem Link
Author: Noszály Áron
Tester: Mark Mikhno
Editorialist: Bhuvnesh Jain
Difficulty
MEDIUM
Prerequisites
DFS, Cycle detection, case analysis.
Problem
You are given a simple graph with N vertices and M edges. Each vertex of the graph can belong to at most one cycle only. For every edge, you need to find the number of simple paths which contain this edge and contain at most one cycle edge in them.
Explanation
The editorial will mainly contain the case analysis through various images and will describe the approach in brief. The exact implementation details can be referred through the editorialist solution which is commented to explain the details in an editorial.
The first thing to do in the problem is to first identify cycle vertices and cycle edges. This is can be simply through DFS or BFS. If you are not aware of this, I recommend you to read through it here. For detailed explanation, Cormen has a very good explanation of it using the concept of back edges and color the vertices into 3 parts white (non-visited), gray (partially-visited) and black (completely visited). If you still have doubts about that, you can ask below. The sample graph which covers all possible corner cases used to describe the editorial is given below.

Now, we run a DFS where we try to split the graph into various trees. The different trees are connected through edges which are part of some cycle in the graph. This means while constructing the tree we will never traverse a cycle edge. At the same time, we will root the all such trees along some vertex and also calculate the subtree size for every vertex as well. The below image shows the output of the algorithm. (This is done as part of dfs function in the implementation). The root of the tree is marked in blacked colour and underlined.
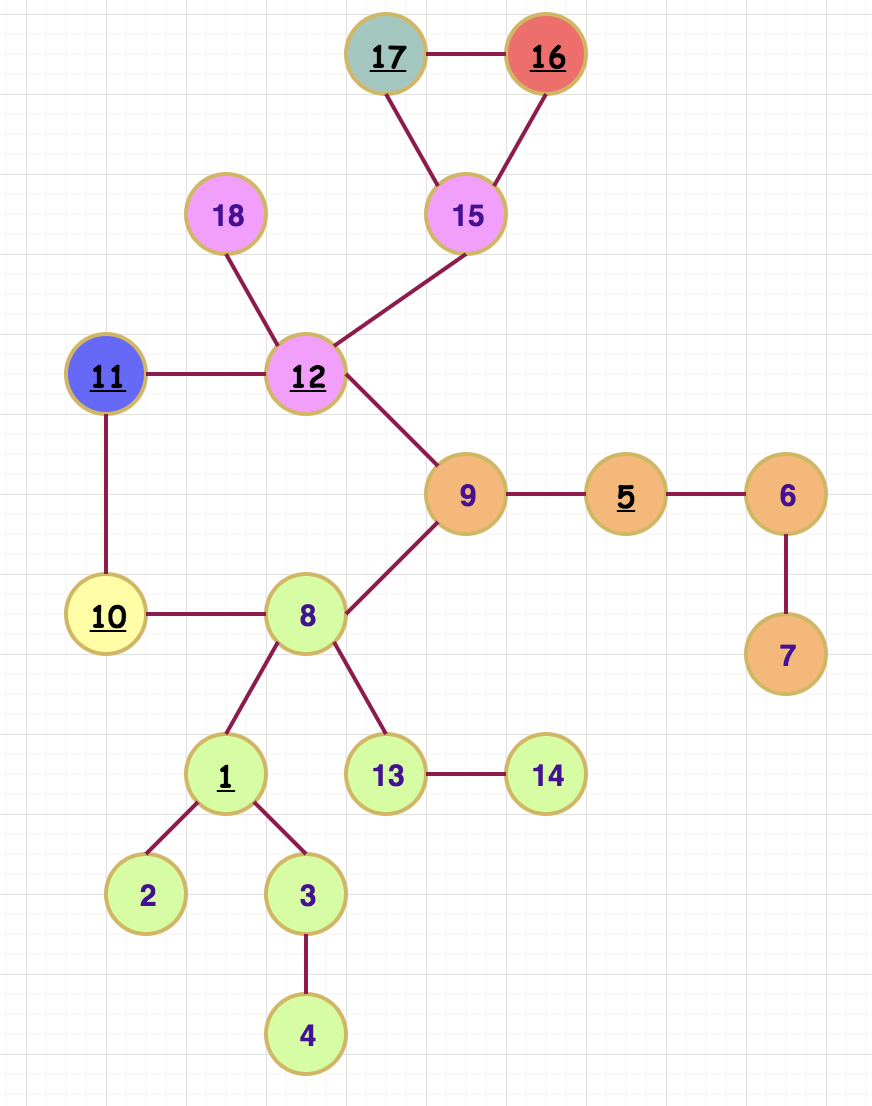
Now, we have 2 cases:
- CYCLE EDGE
Consider the case for edge (8, 9). Since one cycle edge is already included, it means we can only add paths which do not include cycle edges. This is exactly we tried to calculate in the DFS above. So, we basically find the number of vertices (or paths as it is a tree) for both end vertices 8 and 9. The answer is simply the product of these 2 values as it means we chose endpoint from the vertex in tree same as 8 and another end from tree same as 9.
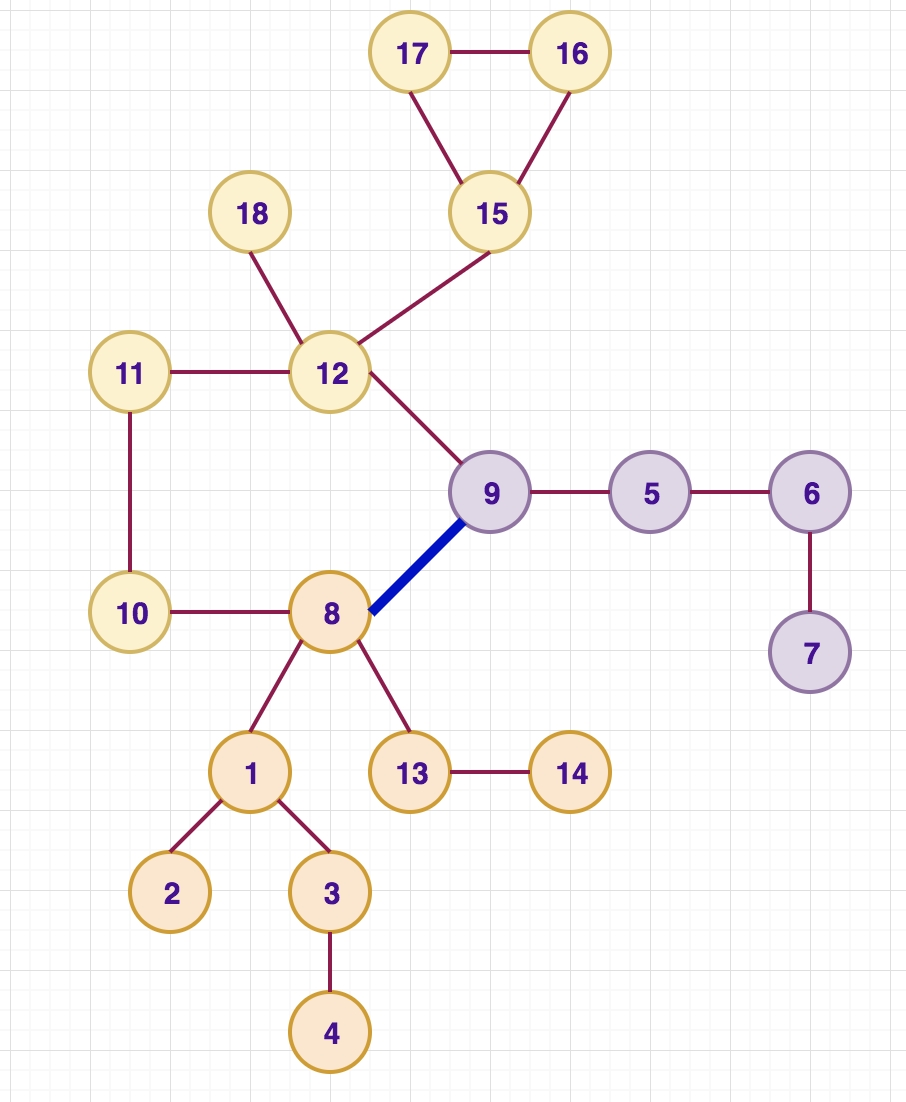
- NON-CYCLE_EDGE
Consider the case for edge (12, 15). We split the answer into two parts: one containing no cycle edge and other containing one cycle edge. For the first case, we simply use the DFS done before. The vertices for starting and ending parts are highlighted in different colours. The answer is simply the product of the number of ways of choosing starting and ending vertices.
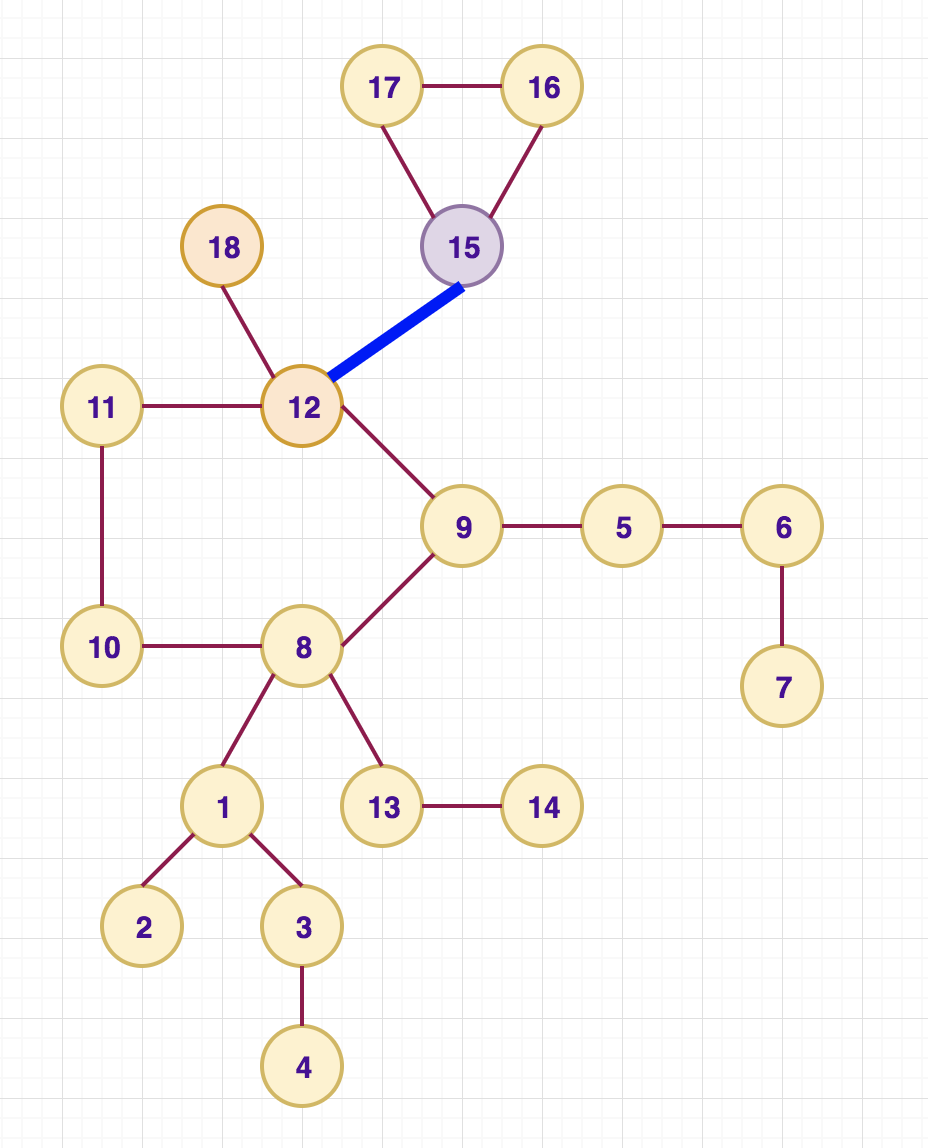
Now for the case when the path contains exactly one edge from a cycle, we again have 2 options. The cycle edge comes from the vertex 12 or from vertex 15. The first case is highlighted in the left image while the second case is highlighted in the right image.
.png)
.png)
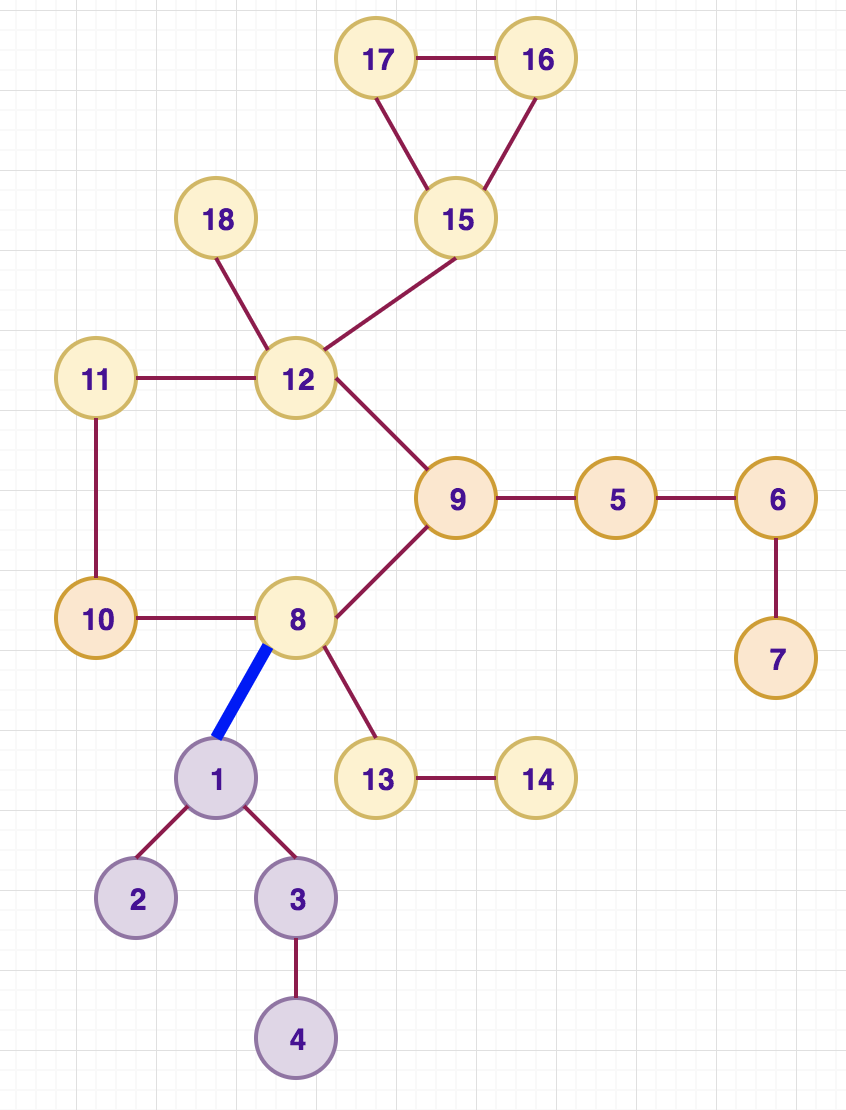
Below figures also highlight how the calculation is done for other non-cycle edges like (1, 8) and (1, 3).
Edge (1, 8). No-cycle path:

Cycle-edge paths (Left: containing cycle as part of vertex 1, Right: containing cycle as part of vertex 8)

Edge (1, 3). No-cycle path:
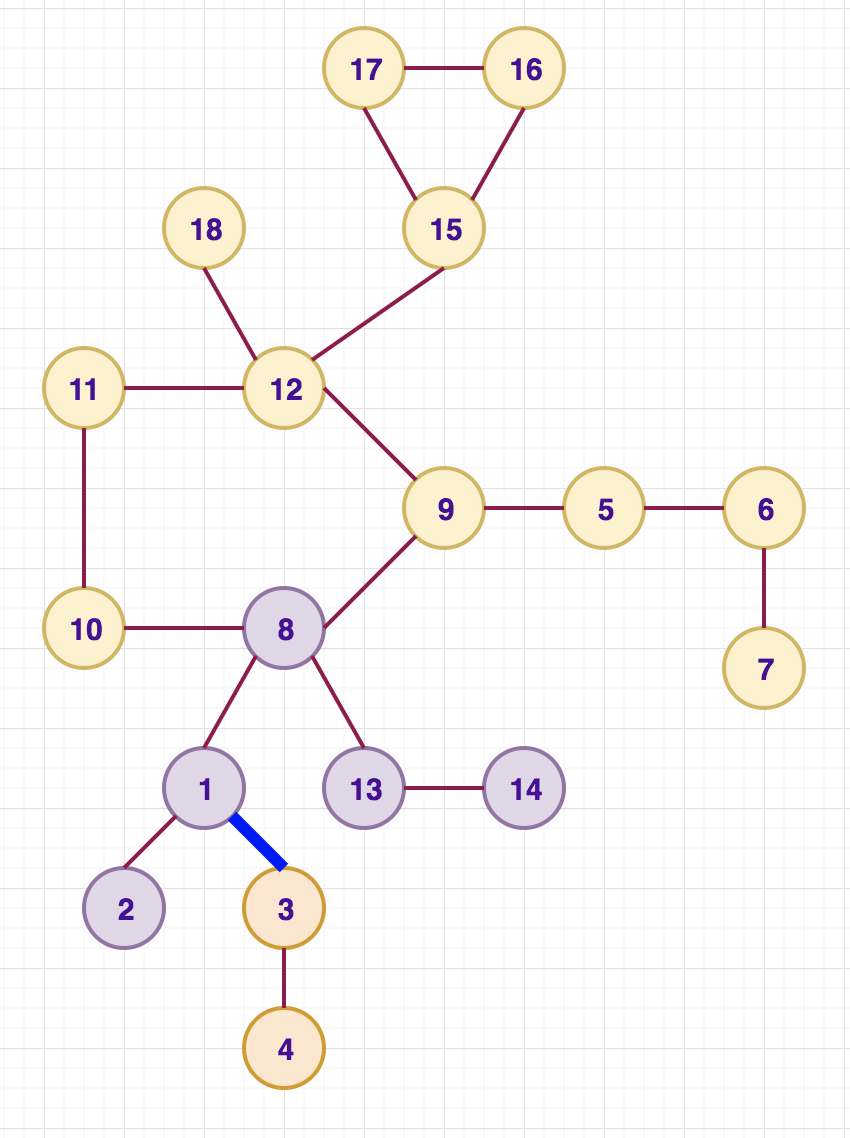
Cycle-edge paths (Left: containing cycle as part of vertex 1, Right: containing cycle as part of vertex 3)
.png)
.png)
The exact details of the above cases can be seen in editorialist implementation. The code is completely commented for your help and is in line with the editorial. The case analysis and what information you store in the nodes can differ and can vary across implementation as well.
Feel free to share your approach, if it was somewhat different.
Bonus Problem
The problem statement doesn’t provide a limit on M, the number of edges. Can you find the upper limit in terms of N?
Time Complexity
O(N + M) per test case.
Space Complexity
O(N + M)
SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here.