PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: sho358
Tester & Editorialist: iceknight1093
DIFFICULTY:
2268
PREREQUISITES:
Multisource dijkstra
PROBLEM:
You’re given an undirected graph on N vertices with M edges.
K mail carriers are present on it: the i-th of them starts at vertex X_i and has a range of D_i; meaning he can deliver mail to any vertex that’s at most distance D_i away from X_i.
Can every vertex receive its mail?
EXPLANATION:
If K = 1, we could run a BFS from the starting point and till distance D_i; and check if all vertices are covered in \mathcal{O}(N + M).
This of course generalizes to a (slow) solution for K \gt 1: run a separate BFS for each mailman and check if all vertices are visited in the end.
Of course, the complexity here is \mathcal{O}(K\cdot (N+M)), which is too slow.
A natural optimization to try now would be to attempt a multisource BFS, however it doesn’t quite work directly because of the D_i values; so a previously visited vertex can’t simply be skipped.
Example
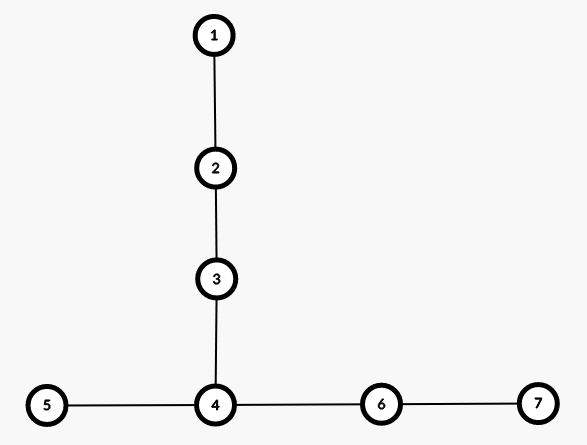
Suppose we have mail carriers at 1 and 5, with D_1 = 5 and D_5 = 4.
If we BFS from 1 first, we’ll end up marking vertices 4 and 6, but not 7.
BFS-ing from 5 will then stop before marking 7, since vertices on its path are already marked.
This case also shows that trying to BFS from vertices with larger D_i first isn’t necessarily correct either.
What really matters is how many moves we have left from each vertex.
In particular, we need to know the maximum number of remaining steps from each vertex.
To do this, we can instead transform our algorithm to a multisource dijkstra!
Let \text{rem}[u] be the maximum number of remaining steps from vertex u.
First, for each mail carrier i, set \text{rem}[K_i] \gets \max(\text{rem}[K_i], D_i).
Then, for a vertex u and an adjacent vertex v, \text{rem}[v] can be updated with \text{rem}[u]-1.
Notice that this is similar to the usual dijkstra with distances, where we update \text{dist}[v] with \text{dist}[u]+wt.
So, simply running dijkstra’s algorithm on this will give us the correct values of \text{rem}[u] for all u.
Note that here, we want to keep the maximum value and not the minimum; make sure to implement that correctly.
Finally, if \text{rem}[u] \leq 0 for any vertex the answer is No; otherwise the answer is Yes.
TIME COMPLEXITY
\mathcal{O}((N+M)\log N) for each testcase.
CODE:
Author's code (C++)
#include <bits/stdc++.h> //Andrei Alexandru a.k.a Sho
using ll=long long;
using ld=long double;
int const INF=1000000005;
ll const LINF=1000000000000000005;
ll const mod=1000000007;
ld const PI=3.14159265359;
ll const MAX_N=3e5+5;
ld const EPS=0.00000001;
#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast")
#define f first
#define s second
#define pb push_back
#define mp make_pair
#define endl '\n'
#define sz(a) (int)a.size()
#define CODE_START ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
ll t,n,m,k,x[200005],d[200005],viz[200005];
vector<ll>g[100005];
void testcase(){
cin>>n>>m>>k;
for(ll i=1;i<=n;i++)
{
viz[i]=0;
}
for(ll i=1;i<=k;i++)
{
cin>>x[i];
}
priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>>q;
for(ll i=1;i<=k;i++)
{
cin>>d[i];
viz[x[i]]=min(-d[i],viz[x[i]]);
q.push(mp(-d[i],x[i]));
}
for(ll i=1;i<=m;i++)
{
ll x,y;
cin>>x>>y;
g[x].pb(y);
g[y].pb(x);
}
while(!q.empty()){
ll x,y;
x=q.top().s;
y=q.top().f;
q.pop();
if(viz[x]!=y){
continue;
}
for(auto it : g[x]){
if(viz[x]+1<viz[it]){
viz[it]=viz[x]+1;
q.push(mp(viz[it],it));
}
}
}
int ans=1;
for(ll i=1;i<=n;i++)
{
if(viz[i]==0){
ans=0;
}
}
if(ans){
cout<<"YES"<<endl;
}else cout<<"NO"<<endl;
for(ll i=1;i<=n;i++)
{
viz[i]=0;
g[i].clear();
}
}
int32_t main(){
CODE_START;
cin>>t;
while(t--){
testcase();
}
}
Editorialist's code (Python)
from heapq import heappop, heappush
for _ in range(int(input())):
n, m, k = map(int, input().split())
pos = list(map(int, input().split()))
dis = list(map(int, input().split()))
adj = [ [] for _ in range(n)]
for i in range(m):
u, v = map(int, input().split())
adj[u-1].append(v-1)
adj[v-1].append(u-1)
dist = [-1] * n
queue = []
for i in range(k):
x, d = pos[i] - 1, dis[i] - 1
dist[x] = max(dist[x], d)
heappush(queue, (-d, x))
while queue:
rem, v = heappop(queue)
rem *= -1
if rem != dist[v] or rem == 0: continue
for x in adj[v]:
if dist[x] < rem - 1:
dist[x] = rem - 1
heappush(queue, (1 - rem, x))
print('Yes' if min(dist) >= 0 else 'No')