PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: Kirtan Shah
Testers: Nishank Suresh, Tejas Pandey
Editorialist: Nishank Suresh
DIFFICULTY:
1432
PREREQUISITES:
Algebraic manipulation
PROBLEM:
You have an array [1, 2, 3, \ldots, N]. At most K times, you can swap any two of its elements. What is the maximum number of inversions the resulting array can have?
EXPLANATION:
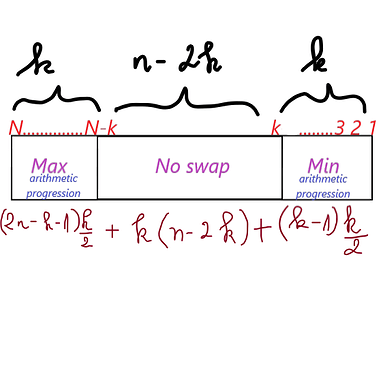
The absolute best final array we can hope for is [N, N-1, N-2, \ldots, 3, 2, 1], which has \binom{N}{2} inversions.
To this end, the optimal sequence of swaps is as follows:
- Swap 1 and N
- Swap 2 and N-1
- Swap 3 and N-2
\vdots
Notice that we need only N/2 swaps to reach [N, N-1, \ldots, 2, 1], so we can set K \gets \min(N/2, K).
Now, simulating the above process in \mathcal{O}(K) is easy, but the constraints don’t allow for it. Instead, let’s analyze it a bit more.
We start out with 0 inversions.
- Swapping 1 and N gives us 2N-3 inversions: N-1 with 1 and N-1 with N, with the pair (1, N) being counted twice
- The same logic should tell you that swapping 2 and N gives us 2N-7 more inversions
- Swapping 3 and N-2 gives us 2N-11 inversions
\vdots
So, K swaps give us
inversions. This is the sum we want to compute.
Doing a bit of basic algebra, this is not hard:
which is an \mathcal{O}(1) formula for the answer!
Of course, it’s possible to derive different formulas with the help of different algebraic manipulations.
TIME COMPLEXITY:
\mathcal{O}(1) per testcase.
CODE:
Setter's code (C++)
#include<iostream>
#include<iterator>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef long double ld;
typedef std::vector<int> vi;
typedef std::vector<ll> vll;
typedef std::vector<ld> vld;
typedef std::vector<std::vector<ll> > vvll;
typedef std::vector<std::vector<ld> > vvld;
typedef std::vector<std::vector<std::vector<ll> > > vvvll;
typedef std::vector<string> vstr;
typedef std::vector<std::pair<ll,ll> > vpll;
typedef std::pair<ll,ll> pll;
#define f(i_itr,a,n) for(ll i_itr=a; i_itr<n; i_itr++)
#define rev_f(i_itr,n,a) for(ll i_itr=n; i_itr>a; i_itr--)
#define pb push_back
#define fi first
#define se second
#define all(a) a.begin(),a.end()
#define ms(a,val) memset(a,val,sizeof(a))
const ll mod = 1000000007;
const ll N = 1e5 + 5;
ll setBitNumber(int n)
{
// calculate the number
// of trailing zeroes
ll k = __builtin_clz(n);
// To return the value
// of the number with set
// bit at (31 - k)-th position
// assuming 32 bits are used
return 1 << (31 - k);
}
void solve()
{
ll n, k;
cin >> n >> k;
if (k >= n / 2) {
cout << (n * (n - 1)) / 2<<endl;
return;
}
ll t = n - k * 2;
cout << (n * (n - 1)) / 2 - (t * (t - 1)) / 2<<endl;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
ll qq_itr=1;
cin >> qq_itr;
while (qq_itr--)
solve();
return 0;
}
Tester's code (C++)
#include <bits/stdc++.h>
using namespace std;
// -------------------- Input Checker Start --------------------
long long readInt(long long l, long long r, char endd)
{
long long x = 0;
int cnt = 0, fi = -1;
bool is_neg = false;
while(true)
{
char g = getchar();
if(g == '-')
{
assert(fi == -1);
is_neg = true;
continue;
}
if('0' <= g && g <= '9')
{
x *= 10;
x += g - '0';
if(cnt == 0)
fi = g - '0';
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if(g == endd)
{
if(is_neg)
x = -x;
if(!(l <= x && x <= r))
{
cerr << "L: " << l << ", R: " << r << ", Value Found: " << x << '\n';
assert(false);
}
return x;
}
else
{
assert(false);
}
}
}
string readString(int l, int r, char endd)
{
string ret = "";
int cnt = 0;
while(true)
{
char g = getchar();
assert(g != -1);
if(g == endd)
break;
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) { return readInt(l, r, ' '); }
long long readIntLn(long long l, long long r) { return readInt(l, r, '\n'); }
string readStringSp(int l, int r) { return readString(l, r, ' '); }
string readStringLn(int l, int r) { return readString(l, r, '\n'); }
void readEOF() { assert(getchar() == EOF); }
vector<int> readVectorInt(int n, long long l, long long r)
{
vector<int> a(n);
for(int i = 0; i < n - 1; i++)
a[i] = readIntSp(l, r);
a[n - 1] = readIntLn(l, r);
return a;
}
// -------------------- Input Checker End --------------------
int main() {
int t;
t = readIntLn(1, 100000);
while(t--) {
long long int n, k;
n = readIntSp(1, 10000000000);
k = readIntLn(1, 10000000000);
if(k*2 < n) k*= 2;
else k = n;
if(k&1) cout << k*((2*n - k - 1)/2) << "\n";
else cout << (k/2)*(2*n - k - 1) << "\n";
}
return 0;
}
Editorialist's code (Python)
def f(x): # 3 + 7 + 11 + ... + x
x = (x+1)//4
return x*(2*x + 1)
for _ in range(int(input())):
n, k = map(int, input().split())
k = min(k, n//2)
print(2*n*k - f(4*k-1))
# ans = (2n-3) + (2n-7) + ... + (2n-4k+1)
We achieve the optimal solution in 
In the Max section, the arithmetic progression is like that: