PROBLEM LINK:
Author: Istvan Nagy
Tester: Kevin Atienza and Gedi Zheng
Editorialist: Kevin Atienza
PREREQUISITES:
Tree center, tree radius, tree diameter, breadth-first search
PROBLEM:
The diameter of an undirected graph is the largest distance between any two nodes in the graph.
Given an unrooted tree, is it possible to decrease the diameter by adding exactly one edge?
QUICK EXPLANATION:
Handle the special case N = 2 (the answer is “NO”). In the following, assume N > 2.
First, find the centers of the tree (in O(N) time). There can be one or two centers.
- If there is only one center, root the tree at the center, and compute the height of each subtree. Let H be the height of the tree. Print “YES” if the root has exactly two children with height H-1, otherwise print “NO”.
- If there are two centers, remove the edge connecting the centers to form two trees, root the two trees on the centers, and compute the heights of all subtrees. Let H be the (common) height of both trees. Print “YES” if one of the roots has exactly one children with height H-1, otherwise print “NO”.
EXPLANATION:
Let us first define a few simple terms related to trees and graphs.
The eccentricity of a node is the largest distance from that node to any other node in the graph.
The diameter of an undirected graph has been defined already. It is the largest distance between any two nodes in the graph. Alternatively, it is the largest eccentricity of any node in the graph. We also call any longest path in the graph a diameter, so the term “diameter” can mean either a path or a number, and it will be clear in context which kind of “diameter” we are referring to.
The radius of an undirected graph is the smallest eccentricity of any node in the graph.
A center of an undirected graph is any node whose eccentricity is equal to the radius. Note that a graph can have many centers (in particular, in a complete graph, all nodes are centers).
Since unrooted trees are a special case of undirected graphs, all the above terms are also defined for them. However, in the case of trees, there are a few additional useful properties:
- If R is the radius and D is the diameter, then R = \lceil D/2 \rceil (i.e. the radius is approximately half the diameter).
- A tree has either one or two centers.
- If there are two centers, then they are connected by an edge.
- All diameters pass through the center(s).
- The diameter is even if and only if there is one center.
These are pretty standard facts and are easy to prove, so we leave this exercise to the reader. The following illustrates the two cases, depending on the number of centers. The blue-filled nodes are the centers, and the blue edges are part of some diameter.
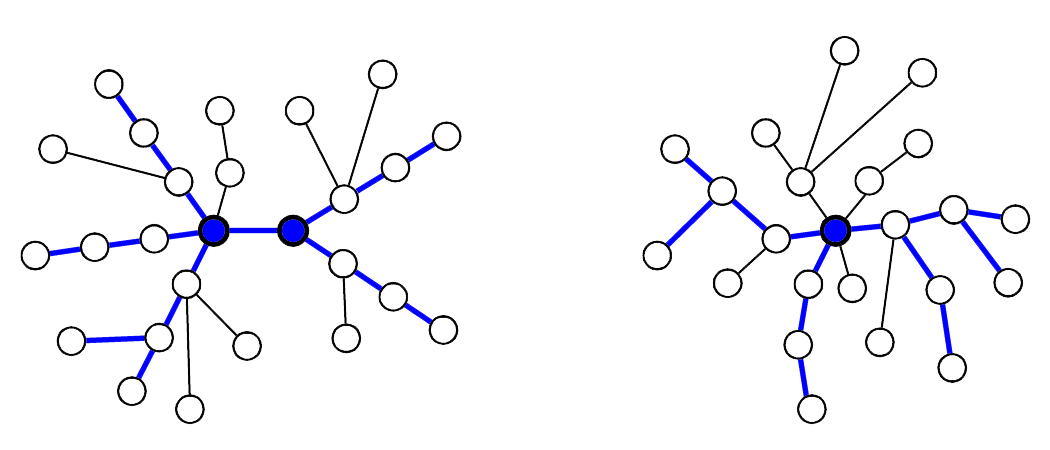
All in all, the facts above say that the circumstances are really nice for an unrooted tree.
Computing the answer
Let’s see how the center, radius and diameter can help us in answering the question. Note that all diameters pass through the center(s), which means that we only have to care about decreasing the lengths of those paths. We handle two cases, depending on whether there are one or two centers.
Case 1: 1 center
Suppose that the tree only contains one center, say C. It makes sense to root the tree on C. Since the graph has at least two nodes, C has at least two children (it cannot have just one, otherwise it wouldn’t be a center). Furthermore, the height of the rooted tree is equal to the radius R of the whole tree, and there are at least two direct subtrees of C whose height is exactly R-1. These facts are intuitive and can easily be proven. See the following for a better picture of the situation:

Suppose there are exactly two direct subtrees of C with height R-1, say A_1 and A_2. In this case, all diameters pass through the sequence of nodes A_1-C-A_2 (or the reverse), and we can decrease the lengths of all these paths by adding an edge from A_1 to A_2, as shown below.
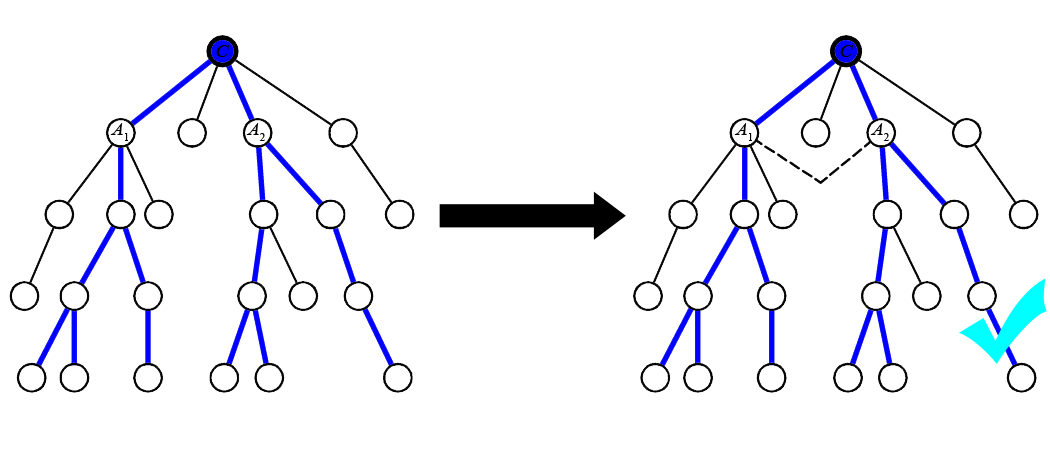
The paths passing through A_1-C-A_2 can instead take a shortcut by passing directly through the new edge, bypassing C. So we conclude that the answer is “YES” if C has exactly two children with height R-1.
What if there are more than two direct subtrees whose height is R-1? Then in this case, we can show that it is impossible to add one edge to decrease the lengths of all diameters. This is because each diameter passes through exactly two of these subtrees, but by adding an edge, we only influence paths that pass through two subtrees, so diameters passing through the remaining trees are not affected.
This is illustrated in the following image, where there are three such children, A_1, A_2, A_3. In all the following cases, try to figure out why there are diameters which are not affected by adding the dashed edge.
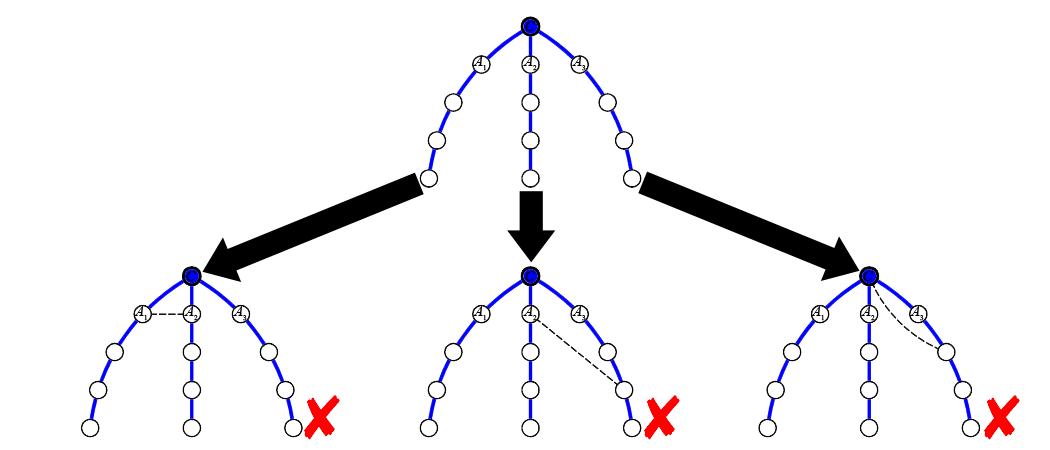
In fact, it is straightforward to prove this fact rigorously. Therefore, we conclude that the answer is “NO” if C has more than two children with height R-1 ![]()
Case 2: 2 centers
We now turn to the case where there are two centers, say C_1 and C_2. In this case, there is an edge between C_1 and C_2. Let’s ignore that edge first, and root the two resulting trees on C_1 and C_2.
Now, we’re sure that C_1 and C_2 has at least one child each, unless the N is exactly two. But if there are just two nodes, we can simply output “NO” (there is only one such case. In fact, this case is given as a sample input). Therefore, we can assume that C_1 and C_2 has at least one child each. We can also show that the heights of both trees are equal. Let H be this common height (note that it is possible to show that H = R-1).
Proceeding as in the above, suppose that C_1 has exactly one child of height H-1, say A. Then in this case it is possible again to decrease the lengths of the diameters by adding an edge from A to C_2, as shown in the following:
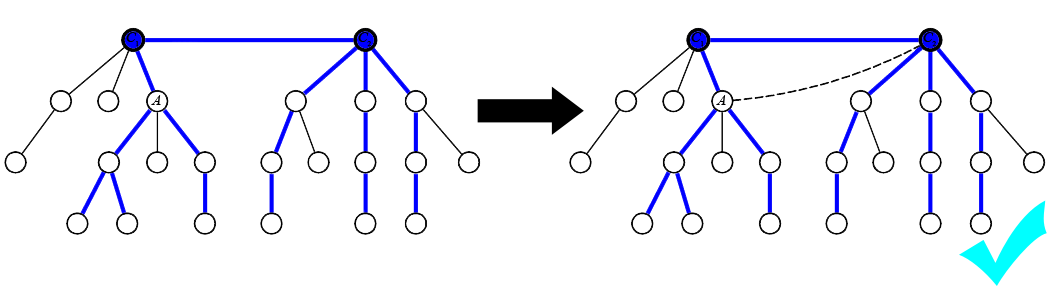
All diameters pass through the node-sequence A-C_1-C_2, but by adding the new edge, the diameters can bypass the node C_1. Therefore, if C_1 has exactly one child of height H-1, then the answer is “YES”. A symmetric argument applies if C_2 has exactly one child of height H-1.
Now, what if C_1 and C_2 both have more than one children of height H-1? Then, similarly as in the previous case, we can show that it is impossible. Consider for example the following case:
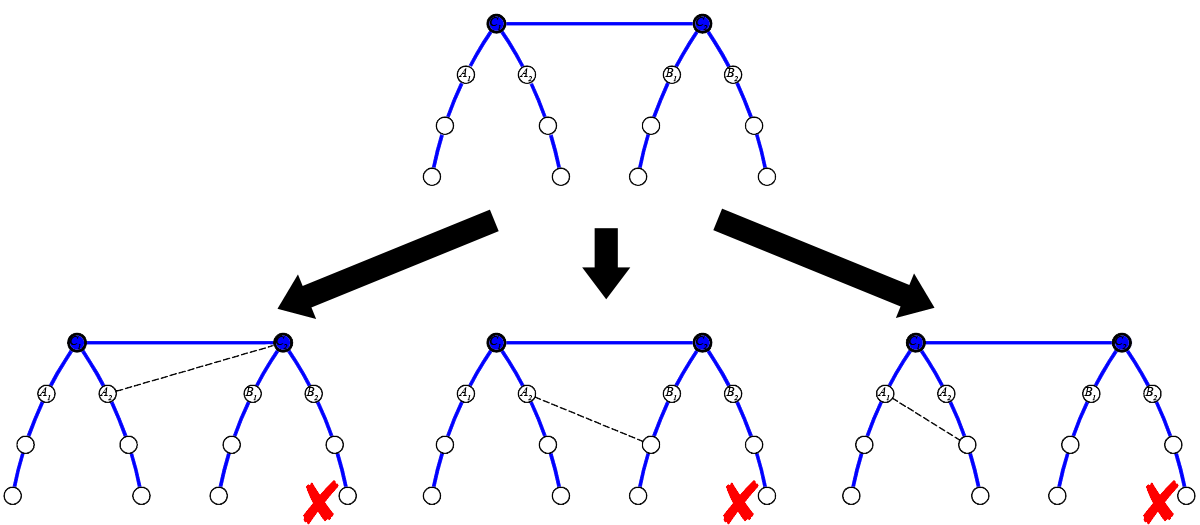
No matter where we place the edge, there are still diameters that are not affected by the new edge. Therefore, the answer is “NO”.
We have handled all the possible cases, and our solution runs in O(N) time (assuming we already know the centers of the tree). This is an optimal solution!
Computing the center
The above algorithm assumes that we have already computed the centers of the tree. How do we compute the centers? There are several well-known ways to do it, some of them running in optimal O(N) time. We will discuss one here:
- Select an arbitrary node X.
- Find the farthest node Y from X. If there is more than one, pick any.
- Find the farthest node Z from Y. If there is more than one, pick any.
- The path Y-Z is now a diameter, so the centers are the centermost nodes on the path from Y to Z (there can be one or two such nodes).
Clearly, this runs in O(N) time. But why does it work? This algorithm relies on the following fact:
For any node, any farthest node from it is an endpoint of some diameter.
Proof:
Let D(i,j) be the distance between nodes i and j.
Let X be any node, and Y be any node with the maximum distance from X. We want to show that Y is the endpoint of some diameter. There are two cases:
- The path X-Y doesn’t intersect any diameter.
- The path X-Y intersects some diameter.
Let’s handle them separately:
Case 1: The path X-Y doesn’t intersect any diameter.
In this case, let A-B be any diameter. Let W be the nearest node from X that belongs in the path A-B, and let V be the farthest node from X in the path X-W that still belongs in the path X-Y. Note that it’s possible that the vertices described here are not distinct. However, we know that nodes V and W are distinct, by assumption. Therefore D(V,W) = D(W,V) \ge 1. The following image illustrates the situation:
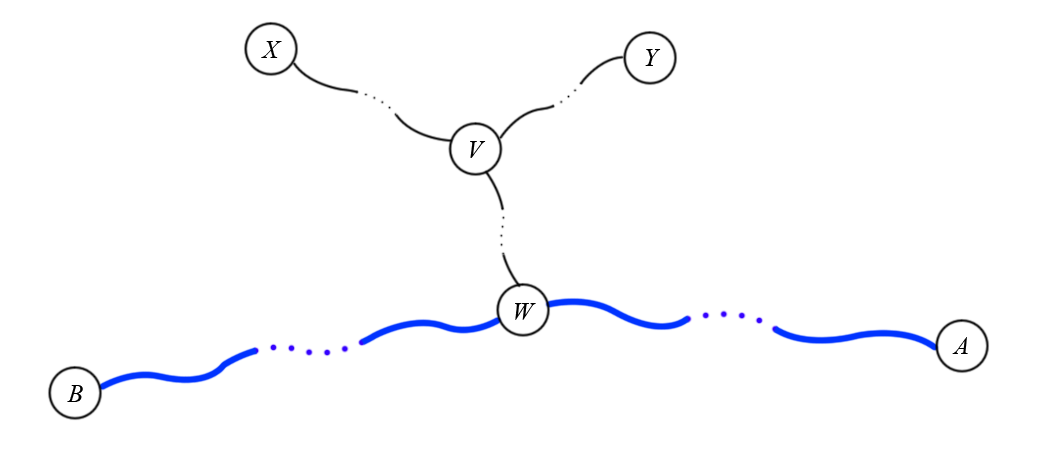
We will show that the path B-Y is longer than the diameter, which is a contradiction (because the diameter is the longest path).
Since Y is farthest from X, we have D(X,A) \le D(X,Y). But we have D(X,A) = D(X,V) + D(V,W) + D(W,A) and D(X,Y) = D(X,V) + D(V,Y), therefore we have:
and
and finally
which shows that B-Y is indeed longer than the diameter A-B. This is a contradiction, therefore this case is impossible.
Case 2: The path X-Y intersects some diameter.
This time, let A-B be a diameter that intersects the path X-Y, and let V and W be the nearest and farthest nodes from X in the path X-Y that are in the diameter A-B, respectively. We also assume that D(W,A) \le D(V,A), i.e. W is nearer to A than V is unless W = V. There is no loss of generality, because otherwise we can just swap A and B. As in the previous case, these nodes are not necessarily distinct. The following image illustrates the situation:
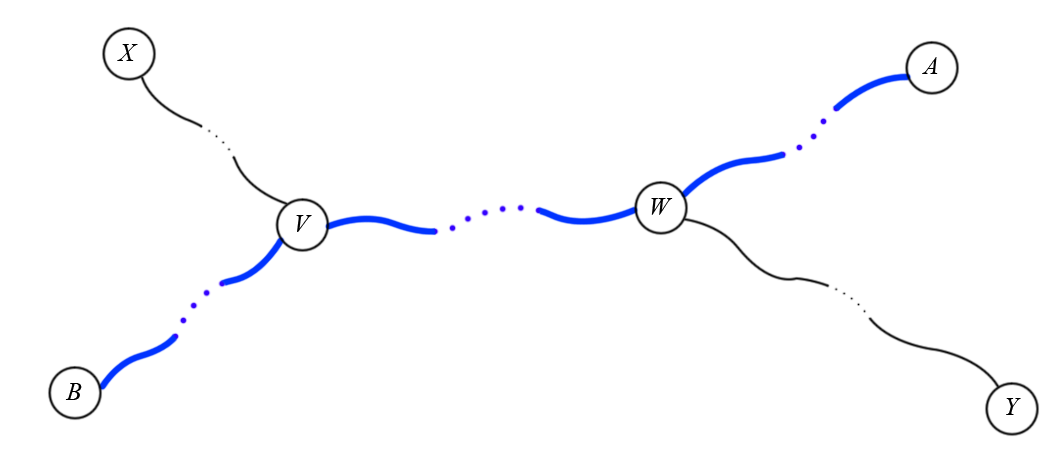
We will now show that the path B-Y is also a diameter, which shows that Y is an endpoint of some diameter.
Since Y is farthest from X, we have D(X,A) \le D(X,Y). But we have D(X,A) = D(X,V) + D(V,W) + D(W,A) and D(X,Y) = D(X,V) + D(V,W) + D(W,Y), therefore we have:
However,
On the other hand, D(B,Y) \le D(B,A) because B-A is a diameter. Therefore, D(B,Y) = D(B,A), and B-Y is also a diameter, and we have shown that Y is an endpoint of some diameter.
Time Complexity:
O(N)


 Actually if we observe your solution minutely using diagrams of this editorial, it covers all the cases described in this editorial nicely
Actually if we observe your solution minutely using diagrams of this editorial, it covers all the cases described in this editorial nicely