Maximum occurred integer in n ranges

help
1

Given n ranges of the form L and R , the task is to find the maximum occurred integer in all the ranges. If more than one such integer exists, print the smallest one.
Task # 1
0 <= L[i] , R[i] < 1000000.
Task # 2
0 <= L[i], R[i] < 1000000000.
Task 1 can be easily done with the below algorithm

  1. Initialize an array arr[] to 0.
  2. For each range i, add +1 at Li index and -1 at Ri of the array.
  3. Find the prefix sum of the array and find the smallest index having maximum prefix sum.
    For task #2 it is impossible to make an array of 1e9 , so how we do that , Help please.
1 Like
2

Source of the problem?

2 Likes
3
4

The main idea, then, is coordinate compression - notice that the only positions you would possibly have to care about are those at the endpoints of updates.

1 Like
5

Or, if you’re lazy, you could copy/paste in a sparse lazy RMQ segment tree :slight_smile: . Probably simpler to do coordinate compression.

1 Like
6

Let us visualize the ranges like this
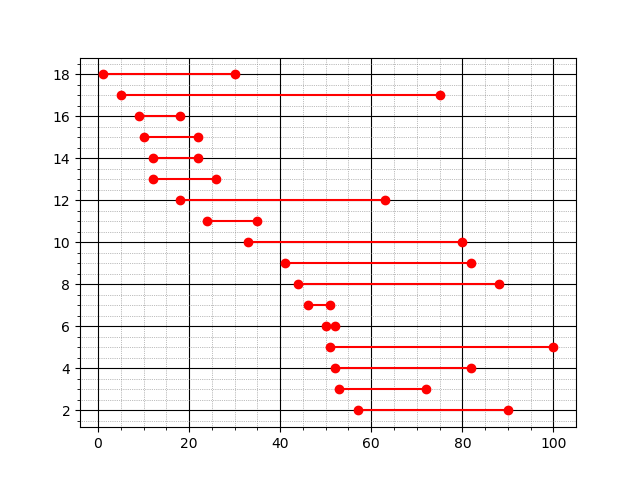
Figure_1

Now the answer will be the the least x which will intersect maximum “red horizontal lines” (ranges). I think you can proceed with Sweep-line technique by storing only the points (both L and R), sorting and then iterating.

I also think that the answer will be one of the points in the given lists (not sure though)

check out this problem and this solution for similar implementation details.

1 Like
7

The hint they give actually reveals a very clean implementation:

code 
/* template */

int main() {
  int Q; cin >> Q;
  map<long long, int> points;
  for (int i = 0; i < Q; i++) {
    long long l, r; cin >> l >> r;
    points[l]++;
    points[r + 1]--;
  }

  int best = 0, cur = 0;
  for (pair<long long, int> x: points) {
    cur += x.second;
    best = max(best, cur);
  }
  cout << best << '\n';
}
1 Like
8

Here, best is the maximum frequency of some integers in whole range (i mean after all queries) but we have to output that integer which is minimum from the all maximum occurred integer. I think this :point_down: would work . btw, Thank you so much :blush:

int  cur = 0, prev = 0, ans;
for (auto  x  :  points) {
     cur += x.second;
     if (cur > prev) {
      ans = x.first;
      prev = cur;
   }
}
cout << ans << '\n';
1 Like