PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Author: Shikhar Sharma
Tester: Shubham Anand Jain
Editorialist: Nishank Suresh
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Centroid decomposition, strongly connected components, dynamic programming on a DAG
PROBLEM:
There is a tree on N vertices, with each vertex X having a value A_X.
It is possible to travel from vertex u to vertex v if and only if d(u, v) = A_u.
Find the maximum possible number of cities Chef can visit by starting at some vertex u and traveling through some sequence of cities, where it is allowed to visit a city multiple times.
QUICK EXPLANATION:
- Use centroid decomposition on the given tree to create an auxillary digraph containing \mathcal{O}(N\log N) vertices and edges which holds all information necessary for knowing which city can be visited from another
- Compress the strongly connected components of this digraph to obtain a dag, where each vertex of the compressed dag is given the value of the number of nodes of the original tree contained in it.
- Dynamic programming on this dag can tell us the maximum number of nodes reachable from any SCC, after which the answer for each node is simply the answer corresponding to its SCC
EXPLANATION
To build intuition for the problem, let us first look at a slow solution.
Let T denote the original tree, and d(u, v) denote the distance between u and v in T.
Suppose we create a directed graph G on n vertices, which contains edge u\rightarrow v iff A_u = d(u, v).
Then, finding the answer for a given vertex u is equivalent to finding the maximum number of vertices reachable on a walk starting from u in G.
This value can be found by compressing G into its strongly connected components and then running a dp on the ensuing dag.
Details
Find the strongly connected components of G and create the condensation graph G_{SCC} (see this if you don’t know how).
Assign to vertex u of G_{SCC} the value C_u, where C_u is the number of vertices in component u.
If f(u) denotes the maximum path starting at component u, we have the recurrence
f(u) = C_u + \max_{(u, v) \in G_{SCC}} f(v)
which is easily computed with dynamic programming - recursion+memoization or considering the nodes in (reversed) topological order both work.
Once f(u) is known for every vertex u, the answer corresponding to vertex v\in G is simply f(comp(v)) where comp(v) is the SCC corresponding to vertex v in G.
Once this is known for every u, simply print the maximum of all such values.
If the original digraph has N nodes and M edges, the complexity of this part is \mathcal{O}(N+M).
This solution is much too slow, because creating G needs us to check every pair of vertices and there is not much hope to improve that because G might have \mathcal{O}(N^2) edges.
However, the idea of creating an auxiliary graph is interesting - perhaps we can create one with less edges but which encapsulates the same amount of information.
A different perspective
Suppose the tree is rooted at some verter r.
Let the children of r be c_1, c_2, \dots, c_k.
Run a dfs from r to find the distance of every vertex from it. This tells us which vertices can be jumped to from r.
Now, given any vertex u \neq r, u must be in the subtree of some c_i. There are then two possibilities for a vertex v such that it is possible to jump from u to v: either v is also within the subtree of c_i, or it is not.
- The case when v is in the subtree of c_i can be computed by recursively considering the subtree rooted at c_i, so we look at the other case
-
v is not in the subtree of c_i, so it must be in the subtree of some other c_j (or equal to r).
Either way, we know for sure that d(r, v) = A_u - d(r, u)
So, u can jump to any vertex not in the subtree of c_i which has a distance of A_u - d(r,u) from u.
Note that we have already calculated the distances of every node from r.
Consider the list of those vertices at distance A_u - d(r, u) from r.
If we have this list ordered in such a way that all the nodes in it lying in the subtree of c_j are together for every 1\leq j\leq k, we notice that u can be joined with all of them except one subarray. In other words, u is joined to a prefix and a suffix of nodes.
Of course, doing it this way is still too slow. if the tree looked like a straight line 1 - 2 - 3 - \dots - n, rooting at 1 and computing things recursively would take \mathcal{O}(N^2) time regardless of the A_u values. Also, we still create upto \mathcal{O}(N^2) edges.
Enter centroid decomposition
As noted above, rooting the tree arbitrarily doesn’t quite work very well.
However, this is where centroid decomposition helps us!
(Don’t know what that is? Take a look at this tutorial or this one)
During the centroid decomposition process, let c be our current centroid.
As above, paths from c to some other vertex can be easily taken care of by running a bfs/dfs from c, so we only need to think about paths from some u\neq c.
Again, as mentioned previously, if we had a (sorted) list of nodes at distance A_u - d(c, u) from c, u needs to be joined to some suffix and some prefix of these nodes.
Doing this naively would be too slow, so let’s perform a small trick.
Let the list of vertices at a given distance D from c be given by L_D.
Suppose L_D = \{x_1, x_2, \dots, x_k\}.
- Create two new sets of nodes p_1, p_2, \dots, p_k and s_1, s_2, \dots, s_k which correspond to the prefixes and suffixes of L_D respectively.
- Add edges p_i \rightarrow p_{i-1} and s_i \rightarrow s_{i+1}, and also p_i \rightarrow x_i and s_i \rightarrow x_i.
- Now, suppose we want to join u to the prefix of nodes x_1, x_2, \dots x_l and the suffix of nodes x_r, x_{r+1}, \dots, x_k where l < r.
It is then enough to create the edges u\rightarrow p_l and u\rightarrow s_r - the connections between prefix and suffix nodes we created earlier will take care of the rest for us.
If you found the above explanation confusing,
A picture is worth a thousand words
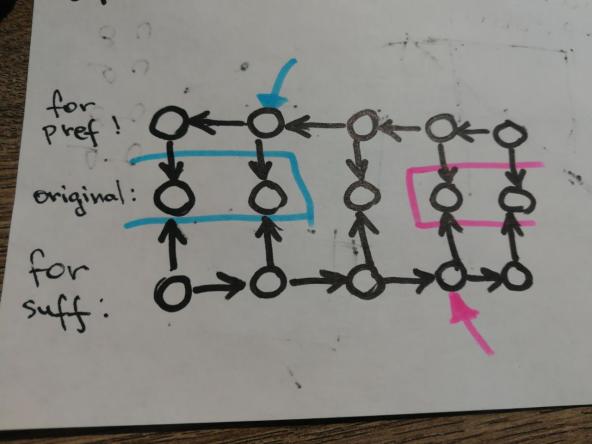
All that remains is to be able to find which prefix and suffix to connect a node to.
This can be done in a couple of ways, generally requiring a little bit of extra bookkeeping.
Details
One way is to note that pushing nodes into L_D in dfs order naturally gives us the ordering we need, so if we also keep information as to which node corresponds to which child of the centroid, it is possible to binary search on the list and find the appropriate prefix/suffix.
This adds an extra \mathcal{O}(\log N) to the time complexity which should still pass well within limits. The setter and editorialist both did this.
it is also possible to replace the binary search with a two-pointer approach where pointers to the appropriate prefix/suffix are maintained for every list L_D.
If the nodes are processed in dfs order, both pointers will only ever increase, so this avoids the extra logarithmic factor from binary search, giving a clean \mathcal{O}(N\log N) solution. This is what the setter’s code does.
Final analysis
Centroid decomposition ensures that the overall complexity of all the dfs-es we perform to find the distance starting from each centroid, is \mathcal{O}(N\log N). This is because each node is only going to be considered in the dfs starting from \mathcal{O}(\log N) centroids.
What about the extra nodes and edges we create?
It turns out that this is also \mathcal{O}(N\log N).
How?
Each time a vertex is considered while processing a centroid, we create two new nodes corresponding to it - one for the prefix, one for the suffix.
So, 2N\log N new nodes are created in total, and we start with N originally.
The number of edges created is similarly small - a list of size k creates 4k-2 edges for the prefix/suffix/node links, and then each vertex creates upto two new edges linking it to some prefix and some suffix whenever it is considered.
Across all lists and nodes, this gives us an upper bound of about 6N\log N on the number of edges created.
We now have an auxiliary graph which has both edges and vertices bounded by \mathcal{O}(N\log N), so running the initially described SCC + dag dp gets us our answer comfortably.
TIME COMPLEXITY:
\mathcal{O}(N\log N) or \mathcal{O}(N\log^2 N) per testcase.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
#include <sys/resource.h>
using namespace std;
vector<vector<int>> adj,dist,new_adj,corr_dist;
vector<int> s,corr_pref,corr_suf,cen_child_num,sorted,levels,vis,root,weight,a;
vector<pair<int,int>> dist_ind;
vector<bool> isit,level_used;
int cc,curr,max_dist,comp;
void dfs(int x,int p)
{
cc++;
s[x]=1;
for(auto y:adj[x])
{
if(y!=p&&!isit[y])
{
dfs(y,x);
s[x]+=s[y];
}
}
}
int find(int x,int p)
{
int ms=0,msin;
for(auto y:adj[x])
{
if(y!=p&&!isit[y])
{
if(s[y]>ms)
{
ms=s[y];
msin=y;
}
}
}
if(ms<=cc/2)
return x;
return find(msin,x);
}
void dfs2(int x, int p, int c, int pc, int l)
{
dist[l].push_back(x);
max_dist=max(max_dist,l);
if(l)
corr_dist[l].push_back(cen_child_num[pc]);
if(a[x]>l)
levels.push_back(a[x]-l);
for(auto y:adj[x])
{
if(y!=p&&!isit[y])
{
if(x==c)
dfs2(y,x,c,y,l+1);
else
dfs2(y,x,c,pc,l+1);
}
}
}
void build(int x, int p, int c, int pc, int l)
{
if(a[x]==l)
{
new_adj[x].push_back(c);
}
if(a[x]>l)
{
int req_l=a[x]-l,pref,suf;
if(req_l<=max_dist&&dist[req_l].size())
{
if(x==c)
{
int node=dist[req_l][0];
int corr_node=corr_suf[node];
new_adj[x].push_back(corr_node);
}
else
{
pref=dist_ind[req_l].first,suf=dist_ind[req_l].second;
while(pref<dist[req_l].size()&&corr_dist[req_l][pref]<cen_child_num[pc])
{
pref=suf+1;
suf=pref+1;
while(suf<dist[req_l].size()&&corr_dist[req_l][suf]==corr_dist[req_l][pref])
suf++;
suf--;
}
if(pref<dist[req_l].size()&&corr_dist[req_l][pref]==cen_child_num[pc])
{
suf=pref+1;
while(suf<dist[req_l].size()&&corr_dist[req_l][suf]==corr_dist[req_l][pref])
suf++;
suf--;
}
if(pref>=dist[req_l].size()||suf<0||corr_dist[req_l][pref]!=cen_child_num[pc])
{
int node=dist[req_l][0];
int corr_node=corr_suf[node];
new_adj[x].push_back(corr_node);
}
else
{
if(pref)
{
int node=dist[req_l][pref-1];
int corr_node=corr_pref[node];
new_adj[x].push_back(corr_node);
}
if(suf<dist[req_l].size()-1)
{
int node=dist[req_l][suf+1];
int corr_node=corr_suf[node];
new_adj[x].push_back(corr_node);
}
}
dist_ind[req_l]={pref,suf};
}
}
}
for(auto y:adj[x])
{
if(y!=p&&!isit[y])
{
if(x==c)
build(y,x,c,y,l+1);
else
build(y,x,c,pc,l+1);
}
}
}
void conn_comp(int x, int n)
{
vis[x]=1;
root[x]=comp;
if(x<=n)
weight[comp]++;
for(auto y:adj[x])
{
if(!vis[y])
conn_comp(y,n);
}
}
void solve(int x)
{
cc=0;
dfs(x,x);
int c=find(x,x);
isit[c]=true;
max_dist=0;
int child_num=0;
for(auto y:adj[c])
{
if(!isit[y])
cen_child_num[y]=child_num++;
}
levels.clear();
dfs2(c,c,c,c,0);
for(int l=0;l<levels.size();l++)
{
int i=levels[l];
if(i>max_dist||level_used[i])
continue;
level_used[i]=true;
int last=-1;
for(auto y:dist[i])
{
corr_pref[y]=curr;
new_adj[curr].push_back(y);
if(last!=-1)
new_adj[curr].push_back(last);
last=curr;
curr++;
}
last=-1;
for(int j=dist[i].size()-1;j>=0;j--)
{
int y=dist[i][j];
corr_suf[y]=curr;
new_adj[curr].push_back(y);
if(last!=-1)
new_adj[curr].push_back(last);
last=curr;
curr++;
}
}
for(int i=0;i<levels.size();i++)
{
if(levels[i]>max_dist)
continue;
level_used[levels[i]]=false;
}
build(c,c,c,c,0);
for(int i=0;i<=max_dist;i++)
{
dist_ind[i]={0,-1};
dist[i].clear();
if(i)
corr_dist[i].clear();
}
for(auto y:adj[c])
{
if(!isit[y])
solve(y);
}
}
void compress(int x)
{
vis[x]=1;
for(auto y:new_adj[x])
{
if(!vis[y])
compress(y);
adj[y].push_back(x);
}
sorted.push_back(x);
}
void starter(int n)
{
sorted.clear();
dist_ind.clear();
s.resize(n+5);
a.resize(n+5);
corr_pref.resize(n+5);
corr_suf.resize(n+5);
cen_child_num.resize(n+5);
adj.resize(n+5);
for(int i=0;i<n+5;i++)
adj[i].clear();
dist.resize(n+5);
for(int i=0;i<n+5;i++)
dist[i].clear();
corr_dist.resize(n+5);
for(int i=0;i<n+5;i++)
corr_dist[i].clear();
dist_ind.resize(n+5,{0,-1});
fill(isit.begin(),isit.end(),false);
isit.resize(n+5,false);
fill(level_used.begin(),level_used.end(),false);
level_used.resize(n+5,false);
int new_n=2*n*(log2(n)+1)+n;
new_adj.resize(new_n+5);
for(int i=0;i<new_n+5;i++)
new_adj[i].clear();
curr=n+1;
comp=0;
}
int main()
{
rlimit R;
getrlimit(RLIMIT_STACK, &R);
R.rlim_cur = R.rlim_max;
setrlimit(RLIMIT_STACK, &R);
int t;
cin>>t;
while(t--)
{
int n,i;
cin>>n;
starter(n);
int x,y;
for(i=0;i<n-1;i++)
{
cin>>x>>y;
adj[x].push_back(y);
adj[y].push_back(x);
}
for(i=1;i<=n;i++)
{
cin>>a[i];
}
solve(1);
curr--;
new_adj.resize(curr+5);
adj.resize(curr+5);
for(i=0;i<n+5;i++)
adj[i].clear();
fill(vis.begin(),vis.end(),0);
vis.resize(curr+5,0);
for(i=1;i<=n;i++)
{
if(!vis[i])
compress(i);
}
for(i=1;i<=curr;i++)
{
vis[i]=0;
new_adj[i].clear();
}
for(i=1;i<=curr;i++)
{
for(auto y:adj[i])
new_adj[y].push_back(i);
}
root.resize(curr+5,-1);
fill(weight.begin(),weight.end(),0);
weight.resize(curr+5,0);
for(i=sorted.size()-1;i>=0;i--)
{
if(!vis[sorted[i]])
{
conn_comp(sorted[i],n);
comp++;
}
}
new_adj.resize(comp+5);
for(i=0;i<comp;i++)
new_adj[i].clear();
for(i=1;i<=curr;i++)
{
for(auto y:adj[i])
{
if(root[y]!=-1&&root[i]!=-1&&root[y]!=root[i])
new_adj[root[y]].push_back(root[i]);
}
}
int dp[comp+5]={0},ans=0;
for(i=0;i<comp;i++)
{
dp[i]+=weight[i];
for(auto y:new_adj[i])
dp[y]=max(dp[y],dp[i]);
ans=max(ans,dp[i]);
}
cout<<ans<<'\n';
}
return 0;
}
Tester's Solution
//By TheOneYouWant
#include<bits/stdc++.h>
#include <sys/resource.h>
#define fastio ios_base::sync_with_stdio(0);cin.tie(0)
using namespace std;
const int LIM = 1e5+5;
const int MAXN = 100050;
const int LOGN = 17;
const int NEWLIM = LIM * 40;
vector<int> adj[LIM], child[LIM], cen_adj[NEWLIM], cen_adj_rev[NEWLIM];
int n;
int a[LIM];
int par[LOGN][MAXN]; // par[i][v]: (2^i)th ancestor of v
int level[MAXN], sub[MAXN]; // sub[v]: size of subtree whose root is v
int ctPar[MAXN]; // ctPar[v]: parent of v in centroid tree
int curr = 0;
bool done[MAXN];
int len[MAXN];
int mark_time[MAXN];
int link[NEWLIM], sz[NEWLIM];
int mxlen[MAXN];
int find(int x){
if(x == link[x]) return x;
return link[x] = find(link[x]);
}
void unite(int a, int b){
a = find(a);
b = find(b);
if(a == b) return;
if(sz[a]<sz[b]) swap(a,b);
link[b] = a;
sz[a] += sz[b];
}
vector<int> used, order, component;
void dfs1(int v){
used[v] = true;
for(int i = 0; i < cen_adj[v].size(); i++){
int u = cen_adj[v][i];
if(!used[u]) dfs1(u);
}
order.push_back(v);
}
void dfs2(int v){
used[v] = true;
component.push_back(v);
for(int i = 0; i < cen_adj_rev[v].size(); i++){
int u = cen_adj_rev[v][i];
if(!used[u]) dfs2(u);
}
}
// calculate level by dfs
void dfsLevel(int node, int pnode) {
for(auto cnode : adj[node]) {
if(cnode != pnode) {
par[0][cnode] = node;
level[cnode] = level[node] + 1;
dfsLevel(cnode, node);
}
}
}
void preprocess() {
level[0] = 0;
par[0][0] = 0;
dfsLevel(0, -1);
for(int i = 1; i < LOGN; i++) {
for(int node = 0; node < n; node++) {
par[i][node] = par[i-1][par[i-1][node]];
}
}
}
int lca(int u, int v) {
if(level[u] > level[v]) swap(u, v);
int d = level[v] - level[u];
// make u, v same level
for(int i = 0; i < LOGN; i++) {
if(d & (1 << i)) {
v = par[i][v];
}
}
if(u == v) return u;
// find LCA
for(int i = LOGN - 1; i >= 0; i--) {
if(par[i][u] != par[i][v]) {
u = par[i][u];
v = par[i][v];
}
}
return par[0][u];
}
int dist(int u, int v) {
return level[u] + level[v] - 2 * level[lca(u, v)];
}
/* Centroid decomposition */
// Calculate size of subtrees by dfs
void dfsSubtree(int node, int pnode) {
sub[node] = 1;
for(auto cnode : adj[node]) {
if(done[cnode]) continue;
if(cnode != pnode) {
dfsSubtree(cnode, node);
sub[node] += sub[cnode];
}
}
}
// find Centroid
int dfsCentroid(int node, int pnode, int size) {
for(auto cnode : adj[node]) {
if(done[cnode]) continue;
if(cnode != pnode && sub[cnode] > size / 2)
return dfsCentroid(cnode, node, size);
}
return node;
}
int fill_dist(int node, int pnode, int target){
int ans = len[node];
for(auto cnode : adj[node]){
if(cnode == pnode) continue;
if(mark_time[cnode] <= mark_time[target]) continue;
len[cnode] = len[node] + 1;
ans = max(ans, fill_dist(cnode, node, target));
}
return ans;
}
vector<pair<int,int>> temp;
void fill_temp(int node, int pnode, int target){
temp.push_back({len[node], node});
for(auto cnode : adj[node]){
if(cnode == pnode) continue;
if(mark_time[cnode] <= mark_time[target]) continue;
fill_temp(cnode, node, target);
}
}
pair<bool, int> bsearch(int ctr, int l, int r, int val){
// find the pref where it works
if(l>r) return {0,0};
while(l < r){
int mid = (l+r+1)/2;
if(mxlen[child[ctr][mid]]>val){
l = mid;
}
else{
r = mid-1;
}
}
bool ans = 1;
if((l!=r) || (mxlen[child[ctr][l]]<val)) ans = 0;
return {ans, l};
}
// Centroid decomposition
void decompose(int node, int pCtr) {
dfsSubtree(node, -1);
int ctr = dfsCentroid(node, node, sub[node]);
if(pCtr == -1){
pCtr = ctr;
mark_time[ctr] = 0;
}
else{
mark_time[ctr] = mark_time[pCtr] + 1;
child[pCtr].push_back(ctr);
}
mxlen[ctr] = 0;
ctPar[ctr] = pCtr;
done[ctr] = 1;
for(auto cnode : adj[ctr]) {
if(done[cnode]) continue;
decompose(cnode, ctr);
}
// update mxlen for all childs
len[ctr] = 0;
mxlen[ctr] = fill_dist(ctr, -1, ctr);
for(int iter = 0; iter < child[ctr].size(); iter++){
int cnode = child[ctr][iter];
temp.clear();
fill_temp(cnode, -1, ctr);
int mx = 0;
for(auto & r : temp){
mx = max(mx, (int)(r.first));
}
mxlen[cnode] = mx;
}
vector<pair<int,int>> nchild;
for(int i = 0; i < child[ctr].size(); i++){
nchild.push_back(make_pair(mxlen[child[ctr][i]], child[ctr][i]));
}
sort(nchild.begin(), nchild.end(), greater<pair<int,int>>());
child[ctr].clear();
for(int i = 0; i < nchild.size(); i++){
child[ctr].push_back(nchild[i].second);
}
int numchild = (int)child[ctr].size() + 1;
int pref[numchild] = {0};
int suff[numchild] = {0};
pref[0] = curr;
int take = 0;
for(int i = 0; i < child[ctr].size(); i++){
take += mxlen[child[ctr][i]];
}
for(int i = 1; i < child[ctr].size();i++){
pref[i] = pref[i-1];
pref[i] += mxlen[child[ctr][i-1]];
}
for(int i = 0; i < child[ctr].size(); i++){
suff[i] = pref[i] + take;
}
int nodes = 2 * take;
// suffix - suffix and prefix - prefix links
for(int j = 0; j < child[ctr].size(); j++){
for(int i = 0; i < mxlen[child[ctr][j]]; i++){
if(j!=0){
int csuff = suff[j] + i;
int nsuff = suff[j-1] + i;
cen_adj[csuff].push_back(nsuff);
}
if((j+1)!=child[ctr].size() && (i < mxlen[child[ctr][j+1]])){
int cpref = pref[j] + i;
int npref = pref[j+1] + i;
cen_adj[cpref].push_back(npref);
}
}
}
for(int iter = 0; iter < child[ctr].size(); iter++){
int cnode = child[ctr][iter];
// start bfs from cnode
temp.clear();
fill_temp(cnode, -1, ctr);
// temp contains children of ctr through cnode
// with their distances
for(auto & r : temp){
if(r.first == a[ctr]){
cen_adj[ctr].push_back(r.second);
}
if(r.first == a[r.second]){
cen_adj[r.second].push_back(ctr);
}
}
for(auto & r : temp){
// node r.second
int val = a[r.second] - r.first - 1;
if(val >= mxlen[ctr]) continue;
if(val < 0) continue;
else{
pair<bool, int> chk = bsearch(ctr, 0, iter-1, val);
if(chk.first){
cen_adj[r.second].push_back(suff[chk.second] + val);
}
if((iter+1 != child[ctr].size()) && (val < mxlen[child[ctr][iter+1]])){
cen_adj[r.second].push_back(pref[iter+1] + val);
}
}
}
// attach with current prefix
for(auto & r : temp){
int val = r.first - 1;
int curr_pref = pref[iter] + val;
cen_adj[curr_pref].push_back(r.second);
}
// attach with current suffix
for(auto & r : temp){
int val = r.first - 1;
int curr_suff = suff[iter] + val;
cen_adj[curr_suff].push_back(r.second);
}
}
curr += nodes;
}
int main(){
fastio;
rlimit R;
getrlimit(RLIMIT_STACK, &R);
R.rlim_cur = R.rlim_max;
setrlimit(RLIMIT_STACK, &R);
int tests;
cin >> tests;
while(tests--){
cin >> n;
// reset all values
for(int i = 0; i < n; i++){
adj[i].clear();
child[i].clear();
link[i] = i;
sz[i] = 1;
mark_time[i] = 1e9;
len[i] = 0;
done[i] = 0;
}
curr = n;
for(int i = 0; i < 40 * n; i++){
cen_adj[i].clear();
cen_adj_rev[i].clear();
}
// done with reset
for(int i = 0; i < n-1; i++){
int u, v;
cin >> u >> v;
u--; v--;
adj[u].push_back(v);
adj[v].push_back(u);
}
for(int i = 0; i < n; i++){
cin >> a[i];
}
preprocess();
decompose(0, -1);
for(int i = 0; i < curr; i++){
for(auto & r : cen_adj[i]){
cen_adj_rev[r].push_back(i);
}
}
for(int i = 0; i < curr; i++){
link[i] = i;
sz[i] = 0;
}
for(int i = 0; i < n; i++){
sz[i] = 1;
}
used.assign(curr, false);
order.clear();
for(int i = 0; i < curr; i++){
if(!used[i]) dfs1(i);
}
used.assign(curr, false);
reverse(order.begin(), order.end());
int dp[curr];
for(int i = 0; i < curr; i++) dp[i] = 0;
for(int i = 0; i < order.size(); i++){
int v = order[i];
if(!used[v]) dfs2(v);
if(component.size()==0) continue;
for(int j = 1; j < component.size(); j++){
unite(component[j-1], component[j]);
}
component.clear();
}
int par[curr];
for(int i = 0; i < curr; i++){
par[i] = find(i);
dp[i] = sz[i];
}
map<pair<int,int>, bool> m;
for(int l = 0; l < order.size(); l++){
int i = order[l];
for(int j = 0; j < cen_adj[i].size(); j++){
int next = cen_adj[i][j];
int a = par[i], b = par[next];
if(a == b) continue;
if(m[make_pair(a,b)]) continue;
m[make_pair(a,b)] = 1;
dp[b] = max(dp[b], dp[a] + sz[b]);
}
}
int ans = 0;
for(int i = 0; i < curr; i++){
ans = max(ans, dp[i]);
}
cout << ans << endl;
}
return 0;
}
Editorialist's Solution
#include "bits/stdc++.h"
#include <sys/resource.h>
// #pragma GCC optimize("O3,unroll-loops")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,mmx,avx,avx2")
using namespace std;
using ll = long long int;
mt19937_64 rng(chrono::high_resolution_clock::now().time_since_epoch().count());
struct centroidDecomp {
vector<vector<int>> G;
vector<int> sz, mark, par, centroid_seq;
centroidDecomp(int n = 0) {
G.assign(n+1, {});
sz.assign(n+1, 0);
mark.assign(n+1, 0);
par.assign(n+1, 0);
}
void addEdge(int u, int v) {
G[u].push_back(v);
G[v].push_back(u);
}
void dfsSize(int u, int v = 0) {
sz[u] = 1;
for (auto x : G[u]) {
if (x == v || mark[x]) continue;
dfsSize(x, u);
sz[u] += sz[x];
}
}
int getCentroid(int u, int p, int n) {
for (auto v : G[u]) {
if (mark[v] || v == p) continue;
if (sz[v] > n/2) return getCentroid(v, u, n);
}
return u;
}
void buildTree(int u = 1, int p = 0) {
dfsSize(u);
int c = getCentroid(u, 0, sz[u]);
centroid_seq.push_back(c);
par[c] = p;
mark[c] = true;
for (auto v : G[c]) {
if (mark[v]) continue;
buildTree(v, c);
}
}
};
// SCC - kactl
// scc(graph, [&] (auto &v) {...})
vector<int> val, comp, z, cont;
int Time, ncomps;
int dfs(int j, auto& g) {
int low = val[j] = ++Time, x; z.push_back(j);
for (auto e : g[j]) if (comp[e] < 0)
low = min(low, val[e] ?: dfs(e,g));
if (low == val[j]) {
do {
x = z.back(); z.pop_back();
comp[x] = ncomps;
cont.push_back(x);
} while (x != j);
cont.clear();
ncomps++;
}
return val[j] = low;
}
void scc(auto& g) {
int n = size(g);
val.assign(n, 0); comp.assign(n, -1); z.clear(); cont.clear();
Time = ncomps = 0;
for (int i = 0; i < n; ++i) if (comp[i] < 0) dfs(i, g);
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
rlimit R;
getrlimit(RLIMIT_STACK, &R);
R.rlim_cur = R.rlim_max;
setrlimit(RLIMIT_STACK, &R);
int t; cin >> t;
while (t--) {
int n; cin >> n;
vector<vector<int>> tree(n+1);
centroidDecomp CD(n);
for (int i = 0; i < n-1; ++i) {
int u, v; cin >> u >> v;
tree[u].push_back(v);
tree[v].push_back(u);
CD.addEdge(u, v);
}
vector<int> a(n+1);
for (int i = 1; i <= n; ++i) {
cin >> a[i];
}
CD.buildTree();
vector<int> mark(n+1), dist(n+1), start_id(n+1), c_id(n+1);
vector<vector<int>> G(n+1);
vector<vector<array<int, 2>>> L;
int node_id = n+1;
auto populate_dist = [&] (const auto &self, int centr, int u, int par) -> void {
if (a[centr] == dist[u]) G[centr].push_back(u);
if ((int)size(L) == dist[u]) L.emplace_back();
for (int v : tree[u]) {
if (mark[v] or v == par) continue;
dist[v] = 1 + dist[u];
self(self, centr, v, u);
}
};
auto populate_L = [&] (const auto &self, int u, int par, int id) -> void {
L[dist[u]].push_back({u, id});
c_id[u] = id;
for (int v : tree[u]) {
if (mark[v] or v == par) continue;
self(self, v, u, id);
}
};
auto create_links = [&] (const auto &self, int u, int par, int centr) -> void {
int child_id = c_id[u];
int dist_to_check = a[u] - dist[u];
if (par != -1 and dist_to_check > 0 and dist_to_check < (int)L.size()) {
// Join to suffix
auto &curL = L[dist_to_check];
auto it = lower_bound(begin(curL), end(curL), array{0, child_id+1}, [](auto &x, auto &y) {
return x[1] < y[1];
});
if (it != end(curL)) {
int node = start_id[dist_to_check] + size(curL) + (it - begin(curL));
G[u].push_back(node);
}
// Join to prefix
it = lower_bound(begin(curL), end(curL), array{0, child_id}, [](auto &x, auto &y) {
return x[1] < y[1];
});
if (it != begin(curL)) {
--it;
int node = start_id[dist_to_check] + (it - begin(curL));
G[u].push_back(node);
}
}
if (par != -1 and dist_to_check == 0) {
G[u].push_back(centr);
}
for (int v : tree[u]) {
if (mark[v] or v == par) continue;
self(self, v, u, centr);
}
};
for (auto centr : CD.centroid_seq) {
L.clear();
dist[centr] = 0;
populate_dist(populate_dist, centr, centr, -1);
int child_id = 0;
for (int child : tree[centr]) {
if (mark[child]) continue;
populate_L(populate_L, child, centr, child_id);
++child_id;
}
for (int d = 1; d < (int)size(L); ++d) {
start_id[d] = node_id;
int s = size(L[d]);
// Prefix nodes are node_id, node_id+1, ..., node_id + s - 1
// Suffix nodes are node_id+s, ..., node_id + 2*s - 1
// Create new nodes
// cerr << "Creating nodes " << node_id << " to " << node_id + 2*s - 1 << " for prefix/suffix of centroid " << centr << " and distance " << d << endl;
for (int _ = 0; _ < 2*s; ++_)
G.emplace_back();
// Create prefix - prefix and suffix - suffix links
for (int i = 0; i+1 < s; ++i) {
G[node_id+i+1].push_back(node_id+i);
G[node_id+s+i].push_back(node_id+s+i+1);
}
// Create prefix-node and suffix-node links
for (int i = 0; i < s; ++i) {
G[node_id+i].push_back(L[d][i][0]);
G[node_id+s+i].push_back(L[d][i][0]);
}
node_id += 2*s;
}
create_links(create_links, centr, -1, centr);
mark[centr] = 1;
}
// G is the auxiliary graph, now SCC + dp
scc(G);
vector<int> ct(ncomps);
vector<set<int>> condensation(ncomps);
for (int i = 1; i <= n; ++i) {
++ct[comp[i]];
}
for (int u = 1; u < node_id; ++u) {
for (int v : G[u]) {
if (comp[u] != comp[v])
condensation[comp[u]].insert(comp[v]);
}
}
vector<int> dp(ncomps);
for (int i = 0; i < ncomps; ++i) {
for (int u : condensation[i])
dp[i] = max(dp[i], dp[u]);
dp[i] += ct[i];
}
cout << *max_element(begin(dp), end(dp)) << '\n';
}
}