PROBLEM LINK:
Practice
Author: (codechefnitj | CodeChef User Profile for Codechef NITJ Chapter | CodeChef)
Editorialist: CodeChefNITJ
DIFFICULTY:
Hard
PREREQUISITES:
2D Fenwick tree, dp
PROBLEM:
find the maximum number of shops you can visit
EXPLANATION:
The first thing to notice is that we can visit shops with an increasing level of royalty and shops are given in ascending order of royalty. So it means we can’t visit any other shop after visiting the last shop provided in the input.
Here, we need to think about the recurrence relation of dp.
Let us say our dp[i], denotes the maximum number of shops that can be visited by ith shop.
and,
dp[i] = max(dp[k])+1, where, i+1<=k<=n and,
k-th shop have x[k] >= x[i] and y[k] >= y[i]
to counter the problem of i+1<=k<=n, we shall traverse the shop from n-th index to 1, such that all the shops will be covered where royalty is higher than i-th shop
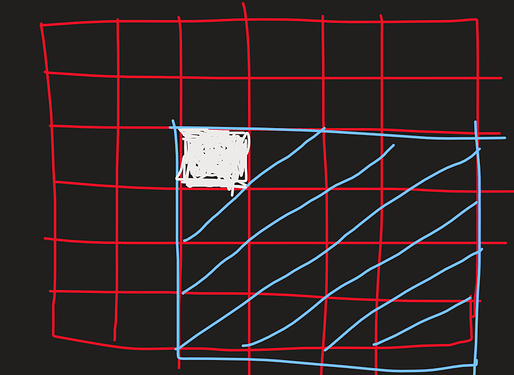
and to counter the problem of x[k] >= x[i] and y[k] >= y[i], we shall use the 2D fenwich tree, which tells us the maximum of the submatrix satisfying above property. Example:
let us say we need to find the dp value for the white-colored shop, so as we have visited all the shops we higher royalty. We just need to find the maximum of blued marked regions and
dp[i] = max(dp[k])+1
and after getting the dp[i] value we shall update the value in Fenwick tree for i-th shop
and our answer will be maximum of all the dp values.
TIME COMPLEXITY:
O(n*log(X*Y)), where X and Y are dimensions of the market
SOLUTIONS:
Editorialist's Solution
#include <bits/stdc++.h>
//#include <boost/multiprecision/cpp_int.hpp>
//using namespace boost::multiprecision;
using namespace std;
#define ll long long int
//#define bint cpp_int
#define pii pair<int, int>
#define REP(i, a, b) for (int i = a; i <= b; i++)
#define RREP(i, a, b) for (int i = a; i >= b; i--)
#define endl "\n"
#define all(x) (x).begin(), (x).end()
#define pi 3.141592653589793238
struct point
{
ll x, y, z;
int index;
point(long long tmp_x = 0, long long tmp_y = 0, long long tmp_z = 0)
{
x = tmp_x;
y = tmp_y;
z = tmp_z;
}
point operator+(point b)
{
return point(this->x + b.x, this->y + b.y, this->z + b.z);
}
point operator-(point b)
{
return point(this->x - b.x, this->y - b.y, this->z - b.z);
}
point operator*(long long val)
{
return point(this->x * val, this->y * val, this->z * val);
}
point operator/(long long val)
{
return point(this->x / val, this->y / val, this->z / val);
}
point &operator=(point b)
{
this->x = b.x;
this->y = b.y;
this->z = b.z;
return *this;
}
point &operator+=(point b)
{
*this = *this + b;
return *this;
}
point &operator-=(point b)
{
*this = *this - b;
return *this;
}
point &operator*=(long long val)
{
(*this) = (*this) * val;
return *this;
}
point &operator/=(long long val)
{
(*this) = (*this) / val;
return *this;
}
bool operator==(point b)
{
if (this->x == b.x && this->y == b.y && this->z == b.z)
return true;
else
return false;
}
};
vector<point> points;
ll dot(point a, point b)
{
ll ans = a.x * b.x + a.y * b.y + a.z * b.z;
return ans;
}
point cross(point a, point b)
{
point e;
e.x = a.y * b.z - b.y * a.z;
e.y = a.z * b.x - b.z * a.x;
e.z = a.x * b.y - b.x * a.y;
return e;
}
double magnitude(point a)
{
return sqrt(dot(a, a));
}
double ang(point a, point b)
{
return acos(dot(a, b) / (magnitude(a) * magnitude(b)));
}
double rad_to_deg(double val)
{
return val * 180 / pi;
}
double deg_to_rad(double val)
{
return val * pi / 180;
}
int direction(point pivot, point a, point b)
{
long long t = cross((a - pivot), (b - pivot)).z;
// t > 0, a x b is anti clockwise
// t < 0, a x b is clockwise
// t == 0, a and b are collinear
return t;
}
#define maxN 100001
#define INF 1000000000
#define mod 1000000007
#define printd(x) cout << fixed << setprecision(10) << x
#define printpoint(p) cout << p.x << " " << p.y << " " << p.z
//int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
//int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
//int dx[] = {-1, 0, 1, 0, 1, -1, 1, -1};
//int dy[] = {0, -1, 0, 1, -1, -1, 1, 1};
ll mulmod(ll a, ll b, ll c)
{
ll x = 0, y = a % c;
while (b > 0)
{
if (b % 2 == 1)
{
x = (x + y) % c;
}
y = (y * 2LL) % c;
b /= 2;
}
return x % c;
}
ll binExp(ll a, ll power, ll m = mod)
{
ll res = 1;
while (power)
{
if (power & 1)
res = mulmod(res, a, m);
a = mulmod(a, a, m);
power >>= 1;
}
return res;
}
int n;
struct shop
{
int x, y;
} arr[maxN];
int ft[1001][1001];
void update2(int index, int val, int x)
{
while (index)
{
ft[x][index] = max(val,ft[x][index]);
index -= (index & -1 * index);
}
}
void update(int index, int val, int y)
{
while (index)
{
update2(y,val,index);
index -= (index & -1 * index);
}
}
int query2(int index, int x)
{
int mx = 0;
while (index <= 1000)
{
mx = max(mx,ft[x][index]);
index += (index & -1 * index);
}
return mx;
}
int query(int index, int y)
{
int mx = 0;
while (index <= 1000)
{
mx = max(mx,query2(y,index));
index += (index & -1 * index);
}
return mx;
}
void solve()
{
cin >> n;
REP(i, 1, n)
{
cin >> arr[i].x >> arr[i].y;
}
int ans=0;
RREP(i,n,1)
{
int mx = query(arr[i].x,arr[i].y)+1;
// cout<<mx<<endl;
ans = max(ans,mx);
update(arr[i].x,mx,arr[i].y);
}
cout<<ans;
}
int main(int argc, char const *argv[])
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// ifstream filptr("input.txt");
// ofstream outpter("output.txt");
// filptr >> input;
// outpter << output;
int t = 1;
//cin >> t;
REP(tc, 1, t)
{
// cout<<"Case "<<tc<<":"<<endl;
solve();
}
//filptr.close();
//outpter.close();
return 0;
}