PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Sayantan Jana
Tester: Felipe Mota
Editorialist: Sayantan Jana
DIFFICULTY:
Easy-Medium
PREREQUISITES:
DFS, Dynamic Programming
PROBLEM:
Given a tree G with N nodes and N-1 undirected edges .
Among all nodes, you can pick a node u and give a direction to each edge in G in a way that node u is reachable from all the nodes in G, to obtain a digraph G’ . It can be proved that the digraph G’ is a Directed Acyclic Graph.
Find the node in G corresponding to whose pick the digraph G’ obtained has maximum or second maximum number of topological sort orderings . Also report the number of topological sort orderings modulo 10^9 + 7 corresponding to those nodes.
QUICK EXPLANATION:
- The number of topological sort orderings corresponding to a node can be found through dynamic programming and DFS fixing the node as root. However the number is quite large to fit in allowed data types.
- However using a similar technique we use in rerooting trick, we can notice that the number of topological sort orderings for a root and its child obeys a simple ratio in terms of their subtree sizes,
- This leads to centroid being the node corresponding to maximum topological sort orderings. The child of centroid with the greatest subtree size corresponds to second maximum topological sort orderings. There can be multiple candidates, pick maximum of them.
- The number of topological sort orderings modulo 10^9 + 7 corresponding to those nodes can be found using dynamic programming and DFS fixing the node as root.
EXPLANATION:
Each of the points in quick explanation is to be discussed in detail here.
Counting number of topological sort orderings corresponding to a given node
We solve the problem : Given an undirected and unrooted tree. We make it rooted by choosing a node as a root. Now we need to find the number of possible orderings of all the nodes in such a way that no ancestor of a node should appear before the node for all the nodes in the rooted tree.
If we solve this, we know the answer for number of topological sort orderings for a node.
Consider the tree in the sample :
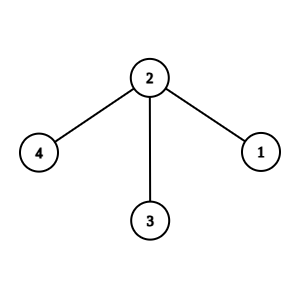
For node 2 as the root, we can have the possible topological orderings: (3,4,1,2), (4,3,1,2), (3,1,4,2), (4,1,3,2), (1,3,4,2) and (1,4,3,2).
Before putting a node in the ordering, we need to put all the nodes in its subtree in the ordering. This is the subproblem that we need to solve, i.e., to solve the above problem for the subtree rooted at the children of the node.
Let us suppose we have solved the subproblem, i.e., we know the number of possible topological sort orderings for each of the subtrees rooted at the children of the node u, denoted by dp[child_1], dp[child_2] … dp[child_c], where c is the number of children of node u.
We can hence find the number of orderings for the concerned subtree rooted at node u. We need to take care of the following points :
- The node u appears at end of ordering.
- The orderings for the subtrees for its children do not lose their relative order (i.e., if 2 nodes a and b appear strictly in the order a…b in the ordering of any of the subtrees for its children, the 2 nodes stay in the same order a…b in the ordering for node u) but can occur in combination with other orderings (i.e., if 2 nodes a and
b appear strictly in the order a…b in the ordering of any of the subtrees for its children, similarly 2 nodes c and d appear strictly in the order c…d in the ordering of any other of the subtrees for its children, they may occur as a…c…b…d, a…b…c…d, c…a…b…d or any other possible way in the ordering for node u such that the relative order that’s decided is not lost).
Hence we arrive at the following relation :
Now that we know the relation, we can make a DFS from the root of the rooted tree to get the required answer for the node.
To solve subtask 1, we can make a DFS from each of the nodes and find the answer for each node. Notice that the count would not be large enough. After getting the count for each node, we can just pick the nodes corresponding to maximum and second maximum count.
Ratio between the number of topological sort orderings for a root and its child as the new root
Say we have found the number of topological sort orderings for a node u and now want to find the same for an adjacent node of u, which occurs as a child of u in the tree rooted at u.
Let node u have c children child_1, child_2 … child_c and we apply rerooting to make child_1 the new root to find number of topological sort orderings for a node child_1.
Let subtree size in the old rooted tree (i.e., the one root at u) be denoted by old\_ssize[] and the subtree size in the new rooted tree (i.e., the one root at child_1) be denoted by new\_ssize[].
On rerooting,
Replace the expression for dp[u] in the above and try simplifying the expression thus obtained to somehow replace a cluster of terms by toposorts_u.
We then notice,
and hence proved is the ratio stated in quick explanation section,
Centroid is the node corresponding to maximum number of orderings
Suppose we are at a node and we want to make a move from the node to one of its children corresponding to which the number of orderings are greater than that for the node.
The child will obey the condition that
This is from the above relation.
This reduces to,
If we keep on making a move like this, we will finally stop at a node which if treated as the root, will have the subtree sizes of each of its children \leq N/2. Hence the required node is the centroid of the tree. Getting the centroid, we can use a DFS and the above DP relation to find the number of orderings modulo 10^9 + 7. This is how we solve subtask 2.
Note that there could be 2 possible centroids in the tree, we choose the maximum between them.
Getting the second maximum
Using the above ratio, we found that centroid corresponds to maximum possible orderings. Further using the same ratio we can realise that whichever node is the contributor for 2-nd maximum needs to be immediately close to the centroid, i.e., be a child of the centroid and also which has the maximum subtree size.
Having maximum subtree size is directly reflected from the ratio, but why exactly the child with maximum subtree size and not any other node in the subtree of that child ? It is because the subtree size of child (let’s say v) can at most be N/2 (cannot be greater else the definition of centroid would be violated). Now any other node in the subtree of v can have at most N/2 - 1 nodes in its subtree and hence it cannot have greater number of orderings than v.
Note, here too we may have multiple candidates, so we need to pick the maximum among them. We can use a DFS and the above DP relation to find the second number of orderings modulo 10^9 + 7.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
const int M = (1<<20)+5;
const int md = 1e9+7;
int sz[M],dp[M],fact[M],inv_fact[M],parent[M];
vector<int> adj[M];
int n;
int pwr(int a,int n,int m)
{
int p = 1;
while(n)
{
if(n&1)
p = 1ll*p*a%m;
a = 1ll*a*a%m;
n >>= 1;
}
return p;
}
void gather_sizes(int u,int par)
{
sz[u] = 1;
parent[u] = par;
for(auto v:adj[u])
{
if(v == par) continue;
gather_sizes(v,u);
sz[u] += sz[v];
}
}
int get_max(int u)
{
int cur_root = u;
bool flag = true;
while(flag)
{
flag = false;
for(auto v:adj[cur_root])
{
if(v == parent[cur_root]) continue;
if(2*sz[v]>n)
{
cur_root = v;
flag = true;
break;
}
}
}
for(auto v:adj[cur_root])
{
if(v == parent[cur_root]) continue;
if(2*sz[v] == n && v>cur_root)
return v;
}
return cur_root;
}
int get_second_max(int u)
{
int mx = 0;
for(auto v:adj[u])
mx = max(mx,sz[v]);
int node = 0;
for(auto v:adj[u])
{
if(sz[v] == mx)
node = max(node,v);
}
return node;
}
int get_topo_count(int u,int par)
{
dp[u] = 1;
sz[u] = 1;
for(auto v:adj[u])
{
if(v == par) continue;
get_topo_count(v,u);
dp[u] = 1ll*dp[u]*dp[v]%md;
dp[u] = 1ll*dp[u]*inv_fact[sz[v]]%md;
sz[u] += sz[v];
}
dp[u] = 1ll*dp[u]*fact[sz[u]-1]%md;
return dp[u];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int L = 500000;
fact[0] = 1;
inv_fact[0] = 1;
for(int i=1;i<=L;++i)
{
fact[i] = 1ll*fact[i-1]*i%md;
inv_fact[i] = pwr(fact[i],md-2,md);
}
int testcases;
cin >> testcases;
while(testcases--)
{
int k;
cin >> n >> k;
for(int i=1;i<n;++i)
{
int u,v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
gather_sizes(1,0);
int max_node = get_max(1);
int max_count = get_topo_count(max_node,0);
int second_max_node = get_second_max(max_node);
int second_max_count = get_topo_count(second_max_node,0);
if(k == 1)
cout << max_node << " " << max_count << "\n";
else
cout << second_max_node << " " << second_max_count << "\n";
for(int i=1;i<=n;++i)
adj[i].clear();
}
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
template<typename T = int> vector<T> create(size_t n){ return vector<T>(n); }
template<typename T, typename... Args> auto create(size_t n, Args... args){ return vector<decltype(create<T>(args...))>(n, create<T>(args...)); }
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
long long TEN(int p){ long long r = 1; while(p--) r *= 10; return r; }
struct union_find {
vector<int> parent;
int n;
union_find(int n) : n(n) { clear(); }
inline void clear(){ parent.assign(n, -1); }
inline int find(int u){ return (parent[u] < 0) ? u : parent[u] = find(parent[u]); }
inline bool same(int u, int v){ return find(u) == find(v); }
inline bool join(int u, int v){
u = find(u);
v = find(v);
if (u != v){
if (parent[u] > parent[v])
swap(u, v);
parent[u] += parent[v];
parent[v] = u;
}
return u != v;
}
inline int size(int u){ return -parent[find(u)]; }
};
template<typename T = int, T mod = 1'000'000'007, typename U = long long>
struct umod{
T val;
umod(): val(0){}
umod(U x){ x %= mod; if(x < 0) x += mod; val = x;}
umod& operator += (umod oth){ val += oth.val; if(val >= mod) val -= mod; return *this; }
umod& operator -= (umod oth){ val -= oth.val; if(val < 0) val += mod; return *this; }
umod& operator *= (umod oth){ val = ((U)val) * oth.val % mod; return *this; }
umod& operator /= (umod oth){ return *this *= oth.inverse(); }
umod& operator ^= (U oth){ return *this = pwr(*this, oth); }
umod operator + (umod oth) const { return umod(*this) += oth; }
umod operator - (umod oth) const { return umod(*this) -= oth; }
umod operator * (umod oth) const { return umod(*this) *= oth; }
umod operator / (umod oth) const { return umod(*this) /= oth; }
umod operator ^ (long long oth) const { return umod(*this) ^= oth; }
bool operator < (umod oth) const { return val < oth.val; }
bool operator > (umod oth) const { return val > oth.val; }
bool operator <= (umod oth) const { return val <= oth.val; }
bool operator >= (umod oth) const { return val >= oth.val; }
bool operator == (umod oth) const { return val == oth.val; }
bool operator != (umod oth) const { return val != oth.val; }
umod pwr(umod a, U b) const { umod r = 1; for(; b; a *= a, b >>= 1) if(b&1) r *= a; return r; }
umod inverse() const {
U a = val, b = mod, u = 1, v = 0;
while(b){
U t = a/b;
a -= t * b; swap(a, b);
u -= t * v; swap(u, v);
}
if(u < 0)
u += mod;
return u;
}
};
using U = umod<>;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int t = readIntLn(1, 5);
while(t--){
int n = readIntSp(1, 5 * TEN(5));
int k = readIntLn(1, 2);
vector<vector<int>> adj(n);
union_find uf(n);
for(int i = 1; i < n; i++){
int u = readIntSp(1, n), v = readIntLn(1, n);
u--; v--;
assert(uf.join(u, v));
adj[u].push_back(v);
adj[v].push_back(u);
}
using ld = long double;
vector<pair<ld, int>> pts;
vector<int> sz(n);
function<void(int, int)> compute = [&](int u, int p){
sz[u] = 1;
for(int v : adj[u]){
if(v == p) continue;
compute(v, u);
sz[u] += sz[v];
}
};
compute(0, -1);
ld val_root = 0;
for(int i = 0; i < n; i++){
val_root += log(sz[i]);
}
function<void(int, int, ld)> fix = [&](int u, int p, ld val){
if(p != -1){
val -= log(sz[u]);
val += log(n - sz[u]);
}
pts.push_back({-val, u});
for(int v : adj[u]){
if(v == p) continue;
fix(v, u, val);
}
};
fix(0, -1, val_root);
sort(pts.rbegin(), pts.rend());
compute(pts[k - 1].second, -1);
U ans = 1;
for(int i = 1; i <= n; i++)
ans *= i;
for(int i = 0; i < n; i++)
ans /= sz[i];
cout << pts[k - 1].second + 1 << ' ' << ans.val << '\n';
}
return 0;
}
