PROBLEM LINK:
Author: Ke Bi
Tester: Kevin Atienza
Translators: Vasya Antoniuk (Russian), Team VNOI (Vietnamese) and Hu Zecong (Mandarin)
Editorialist: Kevin Atienza
DIFFICULTY:
Easy-Medium
PREREQUISITES:
BFS, DFS, Union find, dual graph
PROBLEM:
Given an R\times C grid with W coated walls between some pairs of adjacent cells, what is the minimum number of walls you have to coat so that the grid becomes disconnected?
QUICK EXPLANATION:
The answer can only be 2, 1, 0, or “Chefland is doomed”.
If R\times C = 1, the answer is “Chefland is doomed”.
Consider the endpoints of coated walls as nodes of a graph, and the walls themselves as edges. Also, consider the boundary of the grid as a single node.
If there is a cycle in this graph, then the answer is 0.
If you can add an edge which makes a cycle, the answer is 1. This can be done efficiently using union find or BFS.
Otherwise, the answer is 2.
EXPLANATION:
The only time that the grid can’t be disconnected is when R = C = 1, which means there’s only one bomb. Otherwise, regardless of the configuration, there’s always a way to disconnect the grid using only 2 coatings: simply coat off the walls of one of the corner bombs! (If some of those walls have already been coated, or if the grid has a width or height of 1, then all the better; we will need less than 2 coatings.) This gives us an upper bound of 2 for the answer, and the only problem now is to figure out whether the answer is 2, 1 or 0.
When is the answer 0? This happens when the grid is already disconnected. So given a grid, how do you know if it’s already disconnected? Note that we can’t do a BFS/DFS on the grid because the grid can be very large. Instead, we take a look at some cases of disconnected grids:

What makes these disconnected is that there are “walled-off” sections of the grid. Such a section exists if and only if there is a cycle along the walls! See the following image:

More formally, if we consider the corners of the cells as “nodes” of a graph, and the walls themselves as the edges, then the answer is 0 if and only if there is a cycle in this graph!
Now, you might say there is already a cycle all this time if you consider the boundary of the grid as walls:

But we don’t consider that cycle. To do this in code, simply consider the whole boundary of the grid as a single node.
To find this cycle, we just construct this graph and perform a BFS/DFS on it. So now, we have a fast algorithm to compute whether the answer is 0!
By the way, the graph we constructed is also known as the dual graph of the original graph, in the context of planar graphs.
But if the answer is not 0, then the answer can only be 1 or 2 at this point, and we need to figure out which case it is. So when is the answer equal to 1? The answer is 1 if you can create a cycle along the walls by coating just one wall. For example, in the following images, we can coat one wall each to create a cycle:
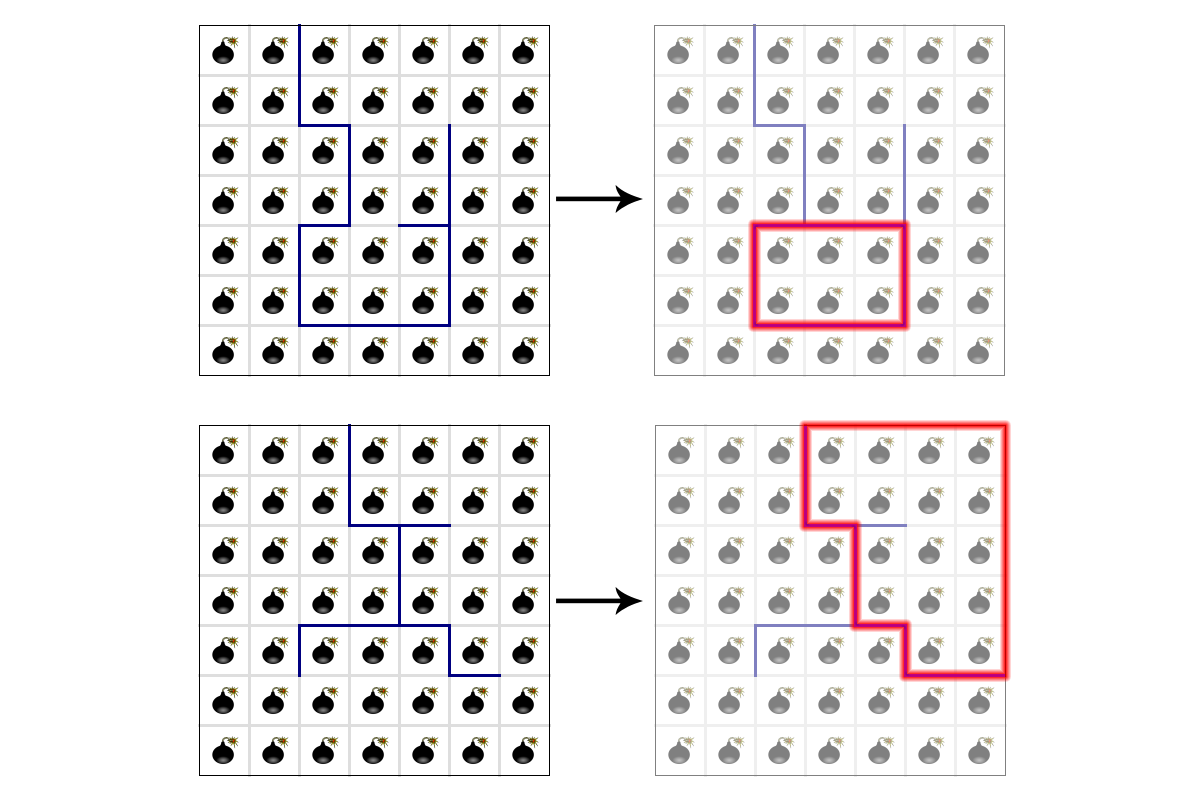
So how do we code this? With BFS also! Here’s one way:
- Perform a BFS on the dual graph, and remember the connected component of each node.
- For each node, try checking each of its four neighbors. If there’s a neighbor in the same connected component but is not already adjacent to the current node, then the answer is 1.
- If we can’t find any, then the answer is 2.
But be careful with implementation! If you implemented it like I mentioned above, where you turn the whole boundary of the grid into a single node, then it’s possible you might get the following case wrong:
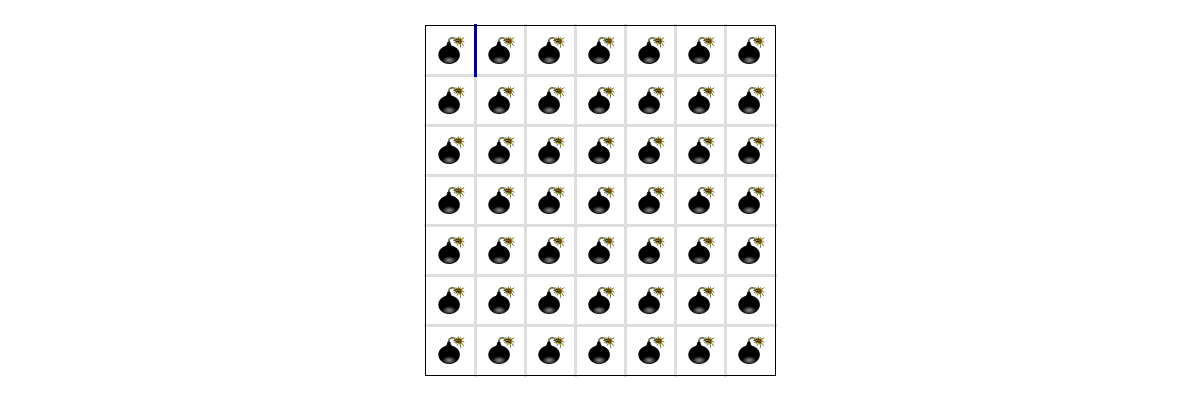
To guard against this test case, just remember the original walls as given in the input.
Another possible case you might get wrong is the following:
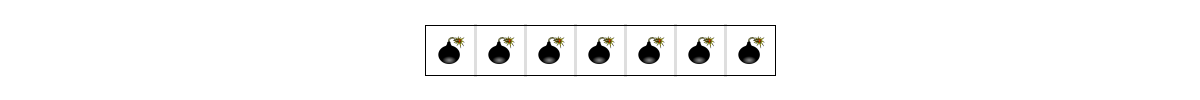
In this case, the answer is 1 because you can coat any vertical wall to disconnect the graph, even though the boundary is represented as a single node.
So now we have an algorithm that runs in O(W \log W) time (because of the usage of maps/sets)! As a final note, you can also use union find to implement the things we described above.
Time Complexity:
O(W \log W)