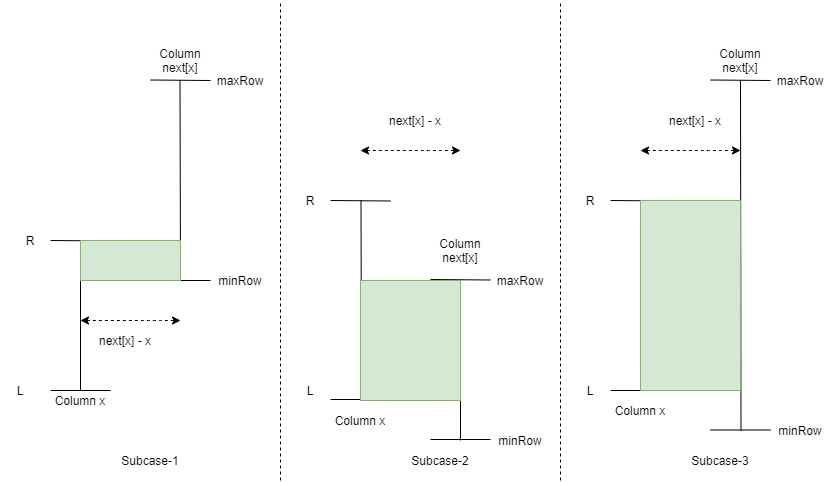PROBLEM LINK:
Practice
Div-1 Contest
Div-2 Contest
Div-3 Contest
Author: Yuriy Fedorov
Testers: Felipe Mota and Radoslav Dimitrov
Editorialist: Vichitr Gandas
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Observations, Math, Combinatorics
PROBLEM:
Given a checkered field of size 10^5 \times 10^5. In this field N different cells (numbered 1 through N) are checkered; for each valid i, the coordinates of the i-th checkered cell are (x_i,y_i). Find minimum possible size of set of cells such that all cells are checkered and each cell is reachable from other cell with minimum possible moves. Also find number of sets with this smallest size.
QUICK EXPLANATION
For every column, find minimum length segment such that it covers all checkered cells of the column. Also find next column which has at least one checkered cell. Now start with the first column, find how many cells need to be checkered to move to the next column. Also calculate number of possible ways to move to the next column. This can be done with maintaining minimum segment for the current column and current set of rows to be marked.
EXPLANATION
For any column, find minimum and maximum row number which are checkered. Lets say they are L and R respectively. Then total number of cells which should be checkered for this column would be R-L+1 because we need to connect row L to row R so that they are in same set ie. they are connected through a path with checkered cells.
Lets say we are currently at column x and current segment of checkered cells for this column is [L, R]. And next column is next[x]. For all other columns j >= next[x], consider all existing checkered cells. Lets say minRow is the minimum row number which has at least one checkered cell and maxRow is the maximum row number which has at least one checkered cell. So now there are three possible scenarios:
Case 1: maxRow < L
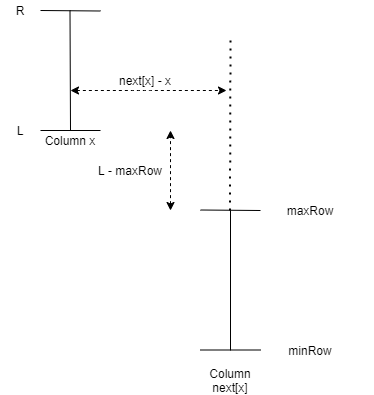
In this case, number of ways to move from column x to next[x] such that all marked cells are in same set with given properties are next[x]-x+L-maxRow \choose next[x]-x.
How
Consider that you are at cell (x_1, y_1) and want to move to cell (x_2, y_2) in a grid. What is total number of paths? Its |x_2-x_1|+|y_2-y_1| \choose |x_2-x_1|. The above problem can also be considered as moving from point (x, L) to point (next[x], maxRow).
Here number of cells which need to be marked to move from column x to column next[x] is simply next[x]-x-1 because consider column x and column next[x] already marked.
Here when we move to column next[x], L, R would change to,
L' = L_{next[x]} and R' = L
Because in column next[x], all cells from L_{next[x]} to L need to be checkered.
Case 2: minRow > R
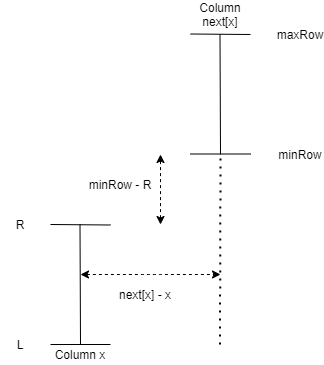
Similar to above case, here number of ways to move from column x to next[x] such that all marked cells are in same set with given properties are next[x]-x+minRow-R \choose next[x]-x.
Here number of cells which need to be marked to move from column x to column next[x] is also next[x]-x-1 as in case-1.
Here when we move to column next[x], L, R would change to,
L' = R and R' = R_{next[x]}
Because in column next[x], all cells from R to R_{next[x]} need to be checkered.
Case 3: When [L,R] overlaps with [minRow, maxRow]
Notice that we have three subcases. In each subcase, the dark area is the region which need to be checkered. In this case, there is only one possible way to move from column x to column next[x] because all the cells in dark area need to be checkered unlike other two cases. In this case number of cells which needs to be checkered to move from column x to next[x] is (min(R, maxRow)-max(L, minRow) + 1) \times (next[x]-x-1).
Here when we move to column next[x], L, R would change to,
L' = min(max(L, minRow), L_{next[x]})
R' = max(min(R, maxRow), R_{next[x]})
In the above mentioned solution, for every column, you will need to maintain next column which have at least one checkered cell. This can be precalculated in \mathcal{O}(N) time.
You also need to maintain minimum segment [L,R] for each column which also can be precalculated in \mathcal{O}(N) time.
You also need to maintain current set of rows which has at least one checkered cell to calculate minRow and maxRow as mentioned in the solution. Once we calculated the number of ways and the number of cells to be checkered, we need to remove the current column rows. These two tasks of maintaining the current set of rows and removing the rows belonging to current column can be done with a multiset in \mathcal{O}(NlogN) time.
Complexity Analysis
Overall time complexity of this solution is \mathcal{O}(NlogN).
Space complexity is \mathcal{O}(N) to maintain next columns, minimum range segment, current set of rows and rows belonging to each column.
Setter's Solution
#include <set>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 228;
const pair<int, int> bad = make_pair(-1, N);
pair<int, int> A[N];
vector<int> used_c[N];
int next[N];
const int MOD = 1e9 + 7;
int fact[2 * N];
int _fact[2 * N];
int powm(int a, int b) {
if (b == 0)
return 1;
if (b % 2 == 1)
return (long long) powm(a, b - 1) * a % MOD;
int z = powm(a, b / 2);
return (long long) z * z % MOD;
}
int C(int n, int k) {
long long res1 = (long long) fact[n] * _fact[k] % MOD;
return (long long) res1 * _fact[n - k] % MOD;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
fill(A, A + N, bad);
fact[0] = 1;
for (int i = 1; i < 2 * N; ++i) {
fact[i] = (long long) fact[i - 1] * i % MOD;
_fact[i] = powm(fact[i], MOD - 2);
}
int n, type;
cin >> n >> type;
multiset<int> now_y;
for (int i = 0; i < n; ++i) {
int x, y;
cin >> x >> y;
A[x].first = max(A[x].first, y);
A[x].second = min(A[x].second, y);
used_c[x].push_back(y);
now_y.insert(y);
}
vector<int> next(N);
int last = N;
for (int i = N - 1; i >= 0; --i) {
next[i] = last;
if (A[i] != bad)
last = i;
}
pair<int, int> now = A[next[0]];
for (int i : used_c[next[0]])
now_y.erase(now_y.find(i));
long long s = now.first - now.second + 1;
int ans = 1;
for (int i = next[0]; i < N; i = next[i]) {
if (next[i] == N)
break;
int mx = *now_y.rbegin();
int mn = *now_y.begin();
if (mx < now.second) {
s += (next[i] - i - 1);
ans = (long long) ans * C(next[i] - i + now.second - mx, next[i] - i) % MOD;
now = make_pair(now.second, A[next[i]].second);
s += now.first - now.second + 1;
} else if (mn > now.first) {
s += (next[i] - i - 1);
ans = (long long) ans * C(next[i] - i + mn - now.first, next[i] - i) % MOD;
now = make_pair(A[next[i]].first, now.first);
s += now.first - now.second + 1;
} else {
now = make_pair(min(now.first, mx), max(now.second, mn));
s += (long long) (now.first - now.second + 1) * (next[i] - i - 1);
now.first = max(now.first, A[next[i]].first);
now.second = min(now.second, A[next[i]].second);
s += now.first - now.second + 1;
}
for (int j : used_c[next[i]])
now_y.erase(now_y.find(j));
}
if (type == 0)
cout << s << '\n';
else
cout << s << ' ' << ans << '\n';
}
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 20);
const int mod = (int)1e9 + 7;
int pw(int x, int p) {
int r = 1;
while(p) {
if(p & 1) r = r * 1ll * x % mod;
x = x * 1ll * x % mod;
p >>= 1;
}
return r;
}
int fact[MAXN];
int ifact[MAXN];
void prepare() {
fact[0] = 1;
for(int i = 1; i < MAXN; i++) {
fact[i] = i * 1ll * fact[i - 1] % mod;
}
ifact[MAXN - 1] = pw(fact[MAXN - 1], mod - 2);
for(int i = MAXN - 2; i >= 0; i--) {
ifact[i] = (i + 1) * 1ll * ifact[i + 1] % mod;
}
}
int n, t, mx;
int l[MAXN], r[MAXN];
void read() {
memset(l, -1, sizeof(l));
cin >> n >> t;
for(int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
chkmax(mx, x);
if(l[x] == -1) {
l[x] = r[x] = y;
} else {
chkmin(l[x], y);
chkmax(r[x], y);
}
}
}
int suff_l[MAXN], suff_r[MAXN];
int C(int n, int k) {
if(n < k || k < 0 || n < 0) return 0;
return (fact[n] * 1ll * ifact[n - k] % mod) * 1ll * ifact[k] % mod;
}
int cnt_paths(int n, int m) {
// n + m - 2 moves
return C(n + m - 2, n - 1);
}
void solve() {
vector<int> li;
for(int i = 1; i <= mx; i++) {
if(l[i] != -1) {
li.pb(i);
}
}
int64_t area = 0;
int cnt = 1;
suff_l[SZ(li) - 1] = l[li.back()];
suff_r[SZ(li) - 1] = r[li.back()];
for(int i = SZ(li) - 2; i >= 0; i--) {
suff_r[i] = max(suff_r[i + 1], r[li[i]]);
suff_l[i] = min(suff_l[i + 1], l[li[i]]);
}
int pref_l = l[li[0]], pref_r = r[li[0]];
for(int i = 0; i < SZ(li) - 1; i++) {
chkmin(pref_l, l[li[i]]);
chkmax(pref_r, r[li[i]]);
area += pref_r - pref_l + 1;
if(suff_r[i + 1] < pref_l) {
cnt = cnt * 1ll * cnt_paths(pref_l - suff_r[i + 1] + 1, li[i + 1] - li[i] + 1) % mod;
area += pref_l - suff_r[i + 1] + li[i + 1] - li[i] - 1;
pref_r = suff_r[i + 1];
} else if (suff_l[i + 1] > pref_r) {
cnt = cnt * 1ll * cnt_paths(suff_l[i + 1] - pref_r + 1, li[i + 1] - li[i] + 1) % mod;
area += suff_l[i + 1] - pref_r + li[i + 1] - li[i] - 1;
pref_l = suff_l[i + 1];
} else {
chkmin(pref_r, suff_r[i + 1]);
chkmax(pref_l, suff_l[i + 1]);
area += (li[i + 1] - li[i] - 1) * 1ll * (pref_r - pref_l + 1);
}
}
chkmin(pref_l, l[li.back()]);
chkmax(pref_r, r[li.back()]);
area += pref_r - pref_l + 1;
if(t) {
cout << area << " " << cnt << endl;
} else {
cout << area << endl;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
prepare();
read();
solve();
return 0;
}
Editorialist's Solution
/***************************************************
@author: vichitr
Compiled On: 13 Feb 2021
*****************************************************/
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 1e5 + 7;
const ll MOD = 1e9 + 7;
const pair<ll, ll> bad = {N, -1};
ll fact[N*2], ifact[N*2];
pair<ll, ll> segment[N];
vector<ll> rows[N];
ll pwr(ll x, ll y)
{
ll r = 1LL;
while(y)
{
if(y & 1)
r = (r * x) % MOD;
y >>= 1;
x = (x * x) % MOD;
}
return r;
}
ll inv(ll x)
{
return pwr(x, MOD - 2ll);
}
ll C(ll n, ll r){
ll ret = fact[n] * ifact[r] % MOD;
return ret * ifact[n - r] % MOD;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(0);
cin.tie(0);
fill(segment, segment + N, bad);
fact[0] = ifact[0] = 1;
for (int i = 1; i < 2 * N; ++i) {
fact[i] = fact[i - 1] * i % MOD;
ifact[i] = inv(fact[i]);
}
int n, t; cin >> n >> t;
multiset<ll> curRows;
for(int i = 0; i < n; i++){
ll x, y; cin >> x >> y;
segment[x].first = min(segment[x].first, y);
segment[x].second = max(segment[x].second, y);
rows[x].push_back(y);
curRows.insert(y);
}
// Find next[i] for all columns i
int last = N;
vector<ll> next(N);
for (int i = N - 1; i >= 0; --i) {
next[i] = last;
if (segment[i] != bad)
last = i;
}
// set current segment for first column
int curColumn = next[0];
pair<ll, ll> curSegment = segment[curColumn];
ll minSetSize = 0;
ll countWays = 1;
// iterate over columns
for(int i = curColumn; i < N; i = next[i]){
// remove current column checkered rows
for(int j: rows[i]){
curRows.erase(curRows.find(j));
}
// increase count of checkered rows for cur column
minSetSize += curSegment.second - curSegment.first + 1;
if(next[i] == N)
break;
// find minRow, maxRow
ll minRow = *curRows.begin();
ll maxRow = *curRows.rbegin();
// find L, R for current sugment
ll L = curSegment.first;
ll R = curSegment.second;
// case -1
if(maxRow < L){
// update set size
minSetSize += next[i] - i - 1;
// update number of ways
countWays *= C(next[i] - i + L - maxRow, next[i] - i);
countWays %= MOD;
// update current segment
curSegment = {segment[next[i]].first, L};
}
// case -2
else if(minRow > R){
// update set size
minSetSize += next[i] - i - 1;
// update number of ways
countWays *= C(next[i] - i + minRow - R, next[i] - i);
countWays %= MOD;
// update current segment
curSegment = {R, segment[next[i]].second};
}
// case -3
else {
// update set size
minSetSize += (min(R, maxRow) - max(L, minRow) + 1) * (next[i] - i - 1);
// update current segment
curSegment = {min(max(L, minRow), segment[next[i]].first), max(min(R, maxRow), segment[next[i]].second)};
}
}
if(t == 0)
cout << minSetSize;
else
cout << minSetSize << " " << countWays;
return 0;
}