MINBRIGE - Editorial

editorial
1

PROBLEM LINK:

Practice
Author: (codechefnitj | CodeChef User Profile for Codechef NITJ Chapter | CodeChef)
Editorialist: CodeChefNITJ

DIFFICULTY:

Hard

PREREQUISITES:

dfs, scc, tree, tree diameter

PROBLEM:

Minimizing the number of bridges in a graph by adding an edge

EXPLANATION:

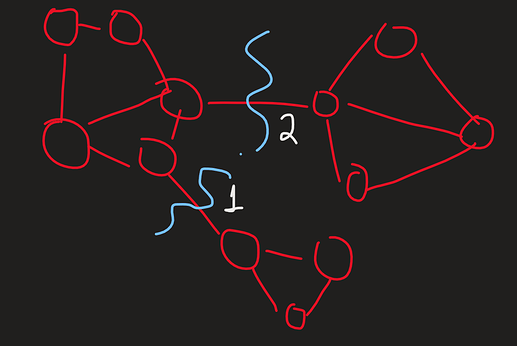
firstly we need to understand what really a bridge is. So any edge in a graph, if removed, increases the total number of connected components.

Example:

Untitled
Untitled1121×752 54.5 KB

here if we remove edge 1 or 2, the total number of connected components increases. Thus, 1 and 2 are bridges.

Now we need to minimize the number of bridges.
So, let us think about the subgraphs between bridges as a single node.

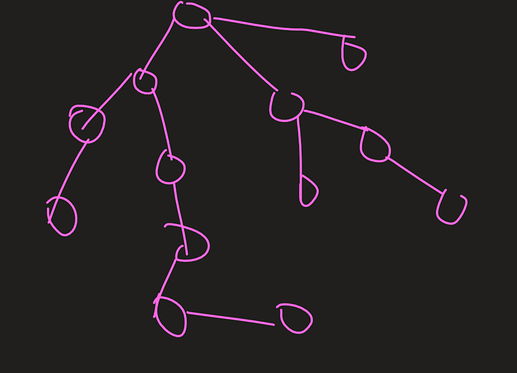
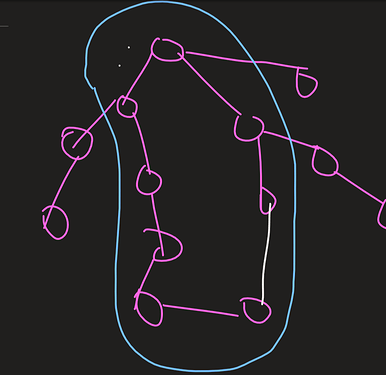
Example:

Untitled
Untitled1211×835 75.9 KB

let us say these marked subgraphs denote a single node and let us convert it into a single node, which can be done using a strongly connected component (SSC).

so, what we get is this:

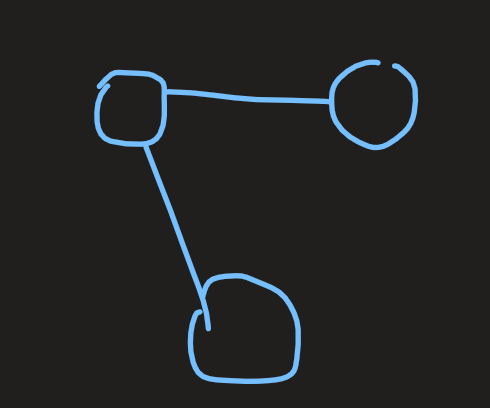
Untitled

Now there is a point to notice, that the reduced graph we got above will always remain a tree (for any other set of data).

So, after reducing the graph we got a tree.

Let us take some other examples of the reduced trees as:

Untitled
Untitled1054×762 68.1 KB

here we need to add an edge between two nodes of the tree such that no bridges are reduced. Firstly each edge of the tree (condensed graph) denotes a bridge, and if we connect any two nodes it will form a cycle and the no of reduced bridges will be the length of the cycle - 1. So,
bridgesRemaining = bridgesPresent - maxLengthOfCycle - 1

So, main task left is to find the max length of a cycle.
And, this length will be equal to the diameter of the tree + 1.

Untitled
Untitled917×889 85.3 KB

So, we are required to find the diameter of tree and our answer will be:
(noOfNodesInCondensedTree-1) - (diameterOfCondensedTree)

TIME COMPLEXITY:

O(n)

SOLUTIONS:

Editorialist's Solution 
#include <bits/stdc++.h>
//#include <boost/multiprecision/cpp_int.hpp>
//using namespace boost::multiprecision;
using namespace std;
#define ll long long int
//#define bint cpp_int
#define mod 1000000007
#define REP(i, a, b) for (int i = a; i < b; i++)
#define maxN 100001
//int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
//int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
//int dx[] = {-1, 0, 1, 0, 1, -1, 1, -1};
//int dy[] = {0, -1, 0, 1, -1, -1, 1, 1};

vector<int> arr[maxN], trans[maxN], stConGraph[maxN], tree[maxN], order;
bool vis[maxN];
int label[maxN], sccCnt;

void dfsn(int node = 1, int par = -1)
{
    vis[node] = true;

    for (int child : arr[node])
    {
        if (child == par)
        {
            continue;
        }
        else if (vis[child])
        {
            stConGraph[node].push_back(child);
            trans[child].push_back(node);
        }
        else
        {
            dfsn(child, node);
            stConGraph[node].push_back(child);
            trans[child].push_back(node);
        }
    }
}

void dfs0(int node)
{
    vis[node] = true;

    for (int child : stConGraph[node])
    {
        if (!vis[child])
        {
            dfs0(child);
        }
    }
    order.push_back(node);
}

void dfs1(int node)
{
    vis[node] = true;

    for (int child : trans[node])
    {
        if (!vis[child])
        {
            dfs1(child);
        }
    }

    label[node] = sccCnt;
}

int nodeX = -1, dis = 0;

void dfsTree(int node = 0, int par = -1, int dep = 0)
{
    if (dis < dep)
    {
        dis = dep;
        nodeX = node;
    }

    for (int child : tree[node])
    {
        if (child == par)
            continue;

        dfsTree(child, node, dep + 1);
    }
}

int main(int argc, char const *argv[])
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int n, m, a, b;
    cin >> n >> m;

    while (m--)
    {
        cin >> a >> b;
        arr[a].push_back(b);
        arr[b].push_back(a);
    }

    dfsn();
    memset(vis, false, maxN);

    for (int i = 1; i <= n; i++)
    {
        if (!vis[i])
        {
            dfs0(i);
        }
    }

    memset(vis, false, maxN);

    for (int i = n - 1; i > -1; i--)
    {
        if (!vis[order[i]])
        {
            dfs1(order[i]);
            sccCnt++;
        }
    }

    if (sccCnt > 1)
    {
        REP(node, 1, n + 1)
        {
            for (int child : arr[node])
            {
                if (child > node)
                {
                    int a = label[child], b = label[node];

                    if (a != b)
                    {
                        tree[a].push_back(b);
                        tree[b].push_back(a);
                    }
                }
            }
        }

        dis = 0, nodeX = 0;
        dfsTree();
        dfsTree(nodeX);

        cout << sccCnt - 1 - dis << endl;
    }
    else
    {
        cout << 0 << endl;
    }

    return 0;
}
1 Like