I just saw a solution using 4 queries. What is the absolute minimum number of queries? Can you prove it?
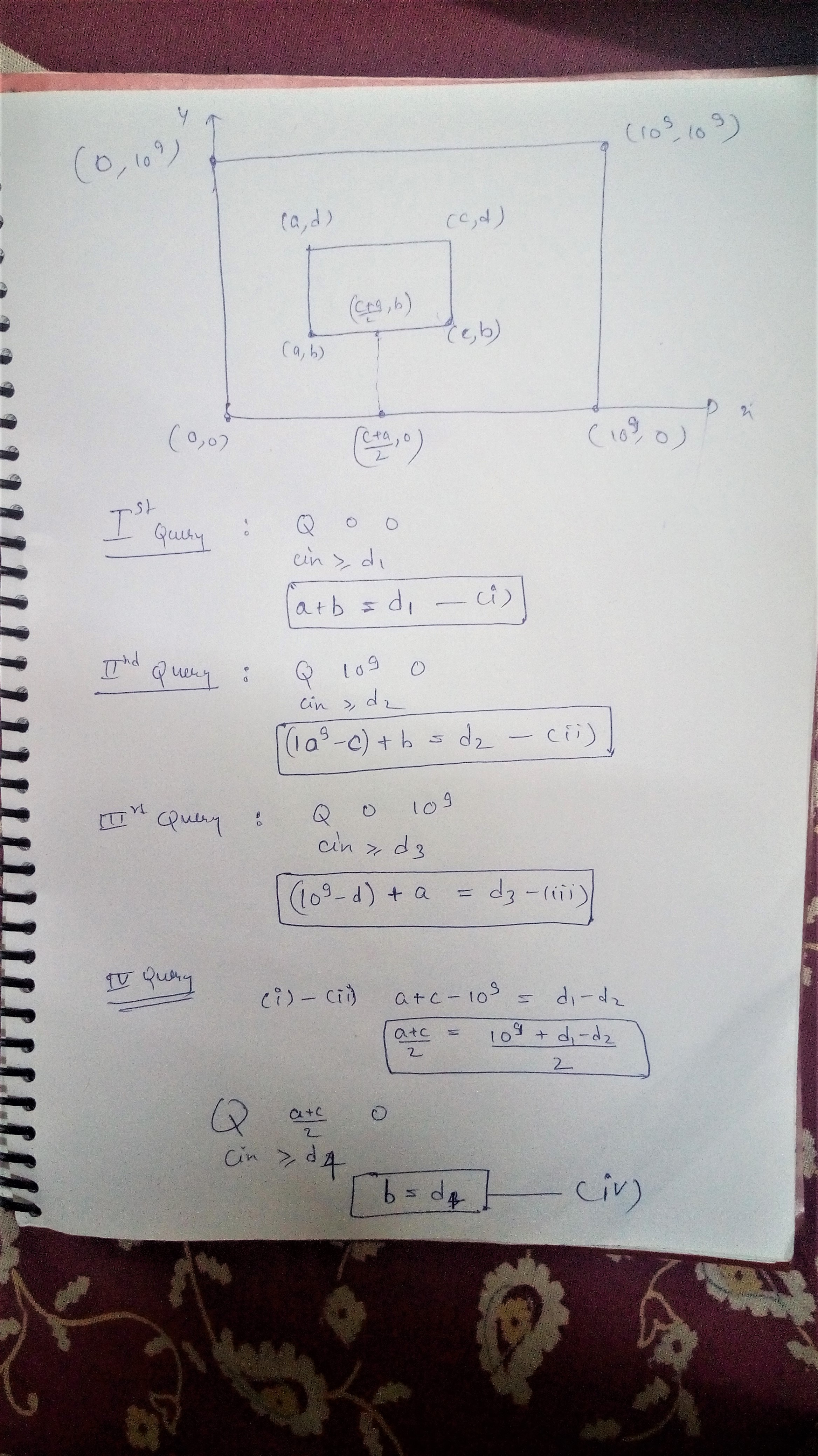
Yes , 4 queries are enough . 3 at 3 corners of given space 1e9x1e9 , and one at mid-point which can be calculated using the results of these 3 queries.
Link: CodeChef: Practical coding for everyone
Regarding Proof , we need 4 linearly independent equations atleast to solve for 4 points . So i think minimum no of queries is 4 only.
I solved it using 4 queries.
Here is the link for My solution using 4 queries
First Query (0,0)
Answer : Z = X_low + Y_low
Now we can form a line between (Z,0) to (0,Z) and lower left point of the rectangle must lie somewhere in the line
Next Query (10^9,0)
Answer : A = 10^9 - X_high + Y_low
Similarly we get another line between ( 10^9-A,0) to (10^9,A)
Now we will find intersection between those two lines and it is guaranteed that lower side of the line will be perpendicular to the point.
Let’s consider intersection points to be (X_temp,Y_temp) and ask query { To be rounded in case of floating point coordinate }
Answer : B
Y_low = Y_temp + B
Other points can be calculated easily. We need to ask 4th Query (10^9,10^9) for that
Aah, that was easy  Thanks!
Thanks!
last equation gives value of b and by using it you can calculate a,c,d