PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Jayesh Shaw
Tester: Abhinav Sharma and Lavish Gupta
Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Sorting, implementation, Pointers.
PROBLEM
You are given two sets of points S and T on the xy-plane. S contains N points and T contains M points.
The points (x_i, y_i) in T have a special property - for every 1\leq i \lt M, x_{i+1} \gt x_i and y_{i+1} \lt y_i.
For each point (x, y) \in T, find the minimum Manhattan distance between (x, y) and a point in S. Formally, for each (x, y) \in T, find \min_{(x_i, y_i) \in S}(|x - x_i| + |y - y_i|)
QUICK EXPLANATION
- For each point in T, we would try to maintain four sets of points, the points lying in each quadrant if the current point was the origin. This way, for each quadrant, we can write the expression for manhattan distance as a formula without absolute signs, and pick the one resulting in the minimum distance.
- When moving from current point to next point, each point at most once moves from down to up, and once from right to left, so each point can move from one set to the other only two times. Hence, the sets can be maintained in O(N*log(N))
EXPLANATION
Let’s focus on the formula of calculating manhattan distance. The distance between two points (x_1, y_1) and (x_2, y_2) is |x_1-x_2| + |y_1 - y_2|. The absolute signs in the formula are disallowing any mathematical observations. Let us try to remove these.
If we have x_1 \leq x_2, the expression becomes x_2-x_1 + |y_2-y_1|. Assuming y_1 \geq y_2, the manhattan distance becomes x_2-x_1 + y_1-y_2. So if we have conditions x_1 \leq x-2 and y_1 \geq y_2, we can write manhattan distance as x_2-x_1+y_1-y_2 = (y_1-x_1) + (x_2-y_2).
Let’s assume we have point (x, y) \in T for which we are calculating the answer. If we have a set of points which are present in S and satsify x_1 \leq x and y_1 \geq y, we can write minimum manhattan distance of (x, y) as (x-y) + \min_{(x_i, y_i) \in S}{ (y_i-x_i)}. We can maintain a multiset of values (y_i - x_i) for all such points, so that we can calculate maximum value of (y_i-x_i) without iterating over all points.
We need to maintain four sets of points for the current point (x, y), where each point in S falls into exactly one category. A point (x_i, y_i) is in
- category one if x_i \leq x and y_i \leq y. The manhattan distance is x-x_i + y-y_i, so we need to find maximum value of -x_i-y_i.
- category two if x_i \geq x and y_i \leq y. The manhattan distance is x_i-x + y-y_i, so we need to find maximum value of x_i-y_i.
- category three if x_i \geq x and y_i \geq y. The manhattan distance is x_i-x + y_i-y, so we need to find maximum value of x_i+y_i.
- category four if x_i \leq x and y_i \geq y. The manhattan distance is x-x_i + y_i-y, so we need to find maximum value of -x_i+y_i.
In mathematical terms, we need to maintain a set of points in each quadrant if point (x, y) is the origin.
Hence, if we have these sets computed for each point in T, we can answer the minimum manhattan distance of that point to any point in S quickly.
Maintaining these sets of points
Let us assume we have already calculated the set for point (x_i, y_i) \in T, and we need to build sets for point (x_{i+1}, y_{i+1}) \in T. Consider following example
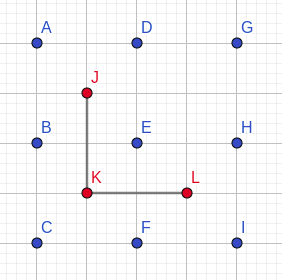
For point J, the sets of points are \{D,G\}, \{A\}, \{B,C\},\{E,F,H,I\} which we have already computed. We need to build these sets for point L.
We can move the origin from J to L by first moving it from J to K and then from K to L. When moving origin from J to K, only points having their y coordinate in range [K_y, J_y] are moved from one set to another. For K, the sets obtained are \{D,G,E,H\}, \{A,B\}, \{C\},\{F,I\}. Similarly, when moving origin from K to L, the only points affected are points with x coordinate in range [K_x, L_x], resulting in sets \{G,H\}, \{A,B,D,E\}, \{C,F\},\{I\} which is the required set of points.
If we can directly process the points with their x coordinate (or y coordinate) is in a specific range quickly without going through all points, we iterate only those times when a point moves from one set to another.
The only time a point moves from one set to another is when it changes the quadrant with respect to the origin. We can see that all points start in the bottom-right quadrant, and move first to either the bottom-left or top-right quadrant and eventually to the top-left quadrant.
We can maintain two copies of S, one sorted by x-coordinate and one sorted by y-coordinate, and maintain one pointer for each copy, denoting the set of points already moved from right to left, and from bottom to top.
Why no point is processed more than twice?
Due to the special property that for every 1\leq i \lt M, x_{i+1} \gt x_i and y_{i+1} \lt y_i for (x_i, y_i) \in T.
This guarantees that every interval [x_i, x_{i+1}] is disjoint for all i, so each point is present in at most one of these, and similarly every interval [y_i, y_{i+1}] is disjoint for all i, so each point is present in at most one of these, resulting in at most two shifts per point.
Implementation
- Maintain two copies of S, one sorted by x-coordinate and one by y-coordinate.
- Maintain four sets of integers, storing the values of \pm x_i \pm y_i depending on which quadrant it is. Initially build these for the first point in T,
- Calculate the answer as the minimum of the distance of (x, y) to point in each set.
- Move the origin from (x_i, y_i) to (x_{i+1}, y_{i+1}) as explained above.
TIME COMPLEXITY
The sorting and the sets take O(N*log(N)) time, leading to overall time complexity O(N*log(N)) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define ll long long int
#define ld long double
#define pb push_back
#define pll pair<ll, ll>
#define tri pair<pll, ll>
#define vl vector<ll>
#define vvl vector< vector<ll> >
#define vlp vector< pair<ll, ll> >
#define vllp vector<pair<pll, ll> >
#define mll map<ll, ll>
#define rep(i,a) for(ll i=0; i< a; i++)
#define rep1(i,a) for(ll i = 1; i< a; i++)
#define foi(i, a, b) for(ll i = a; i<b ; i++)
#define fod(i, a, b) for(ll i = a; i>=b ; i--)
#define mp make_pair
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
#define fst first
#define sec second
#define ff first.first
#define fs first.second
#define max3(a, b, c) max(max(a, b), c)
#define min3(a, b, c) min(min(a, b), c)
#define MAX 100005
#define MOD 1000000007
// #define MOD 998244353
#define endl "\n"
#define INF (ll)1e18
#define s(v) (ll)v.size()
#define e(v) v.empty()
#define bscount(x) __builtin_popcountll(x)
// #define ordered_set tree<int, null_type,less<int>, rb_tree_tag,tree_order_statistics_node_update>
using namespace std;
// using namespace __gnu_pbds;
void __print(ll x) {cerr << x;}
void __print(ld x) {cerr << x;}
void __print(char x) {cerr << '\'' << x << '\'';}
void __print(const char *x) {cerr << '\"' << x << '\"';}
void __print(const string &x) {cerr << '\"' << x << '\"';}
void __print(bool x) {cerr << (x ? "true" : "false");}
template<typename T, typename V>
void __print(const pair<T, V> &x) {cerr << '{'; __print(x.first); cerr << ','; __print(x.second); cerr << '}';}
template<typename T>
void __print(const T &x) {int f = 0; cerr << '{'; for (auto &i: x) cerr << (f++ ? "," : ""), __print(i); cerr << "}";}
void _print() {cerr << "]\n";}
template <typename T, typename... V>
void _print(T t, V... v) {__print(t); if (sizeof...(v)) cerr << ", "; _print(v...);}
#ifndef ONLINE_JUDGE
#define debug(x...) cerr << "[" << #x << "] = ["; _print(x)
#else
#define debug(x...)
#endif
ll gcd(ll a, ll b){if(b==0)return a;return gcd(b, a%b);}
ll cpow(ll a, ll b, ll M){ll ans = 1;while(b){if(b&1) ans = ans*a%M; b/=2;a=a*a%M;}return ans;}
void ingraph(vvl& graph, ll m){ll x, y;rep(i, m){cin>>x>>y;x--, y--;graph[x].pb(y);graph[y].pb(x);}}
ll modify(ll n){ll res = n;res%=MOD;res+=MOD;res%=MOD;return res;}
ll fexp(ll a, ll b) {return cpow(a, b, MOD);}
ll cinv(ll a, ll p){return cpow(a, p-2, p);}
ll inverse(ll a) {return cinv(a, MOD);}
vvl tree(4, vl(4*MAX, INF));
vvl lazy(4, vl(4*MAX, 0));
void push(ll nt, ll cur){
tree[nt][2*cur + 1] += lazy[nt][cur];
tree[nt][2*cur + 2] += lazy[nt][cur];
lazy[nt][2*cur + 1] += lazy[nt][cur];
lazy[nt][2*cur + 2] += lazy[nt][cur];
lazy[nt][cur] = 0;
}
void build(ll nt, vl& vec, vl& init, ll cur, ll l, ll r){
if(l == r){
if(nt == init[l]){
tree[nt][cur] = vec[l];
}
return;
}
ll mid = l + (r - l)/2;
build(nt, vec, init, 2*cur + 1, l, mid);
build(nt, vec, init, 2*cur + 2, mid+1, r);
tree[nt][cur] = min(tree[nt][2*cur + 1], tree[nt][2*cur + 2]);
}
void posupd(ll nt, ll cur, ll l, ll r, ll pos, ll val){
if(l == r && l == pos){
tree[nt][cur] = val;
return;
}else if(l > pos || r < pos) return;
ll mid = l + (r - l)/2;
push(nt, cur);
posupd(nt, 2*cur + 1, l, mid, pos, val);
posupd(nt, 2*cur + 2, mid+1, r, pos, val);
tree[nt][cur] = min(tree[nt][2*cur + 1], tree[nt][2*cur + 2]);
}
void add(ll nt, ll val){
tree[nt][0] += val;
lazy[nt][0] += val;
}
ll report(){
ll ans = INF;
rep(i, 4) ans = min(ans, tree[i][0]);
return ans;
}
ll getMsk(pll a, pll b){
ll ans = 0;
ans |= (b.fst > a.fst);
ans |= ((b.sec < a.sec)<<1);
return ans;
}
ll manhattan(pll a, pll b){
return abs(a.fst - b.fst) + abs(a.sec - b.sec);
}
int main(){
// #ifndef ONLINE_JUDGE
// freopen("../testCases/tc13.txt", "r", stdin);
// freopen("../myOut/out13.txt", "w", stdout);
// #endif
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
ll n, m;
cin>>n>>m;
vlp pts(n), ndm(m);
vl x(m), y(m);
rep(i, n) cin>>pts[i].fst>>pts[i].sec;
rep(i, m){
cin>>ndm[i].fst>>ndm[i].sec;
x[i] = ndm[i].fst;
y[i] = -ndm[i].sec;
}
vl init(n);
vl dis(n);
rep(i, n){
init[i] = getMsk(ndm[0], pts[i]);
dis[i] = manhattan(pts[i], ndm[0]);
}
rep(i, 4) build(i, dis, init, 0, 0, n-1);
vector<vector<tri> > transitions(m);
rep(i, n){
ll xidx = lower_bound(all(x), pts[i].fst) - x.begin() - 1;
ll yidx = lower_bound(all(y), -pts[i].sec) - y.begin() - 1;
if(xidx == yidx){
if(xidx == m-1 || xidx < 0) continue;
else{
transitions[xidx].pb({{getMsk(ndm[xidx], pts[i]),\
getMsk(ndm[xidx + 1], pts[i])}, i});
}
}
else{
if(xidx != m-1 && xidx >= 0){
transitions[xidx].pb({{getMsk(ndm[xidx], pts[i]),\
getMsk(ndm[xidx + 1], pts[i])}, i});
}
if(yidx != m-1 && yidx >= 0){
transitions[yidx].pb({{getMsk(ndm[yidx], pts[i]),\
getMsk(ndm[yidx + 1], pts[i])}, i});
}
}
}
rep(i, m){
cout<<report()<<endl;
if(i < m-1){
add(0, ndm[i+1].fst - ndm[i].fst + ndm[i].sec - ndm[i+1].sec);
add(1, - ndm[i+1].fst + ndm[i].fst + ndm[i].sec - ndm[i+1].sec);
add(2, ndm[i+1].fst - ndm[i].fst - ndm[i].sec + ndm[i+1].sec);
add(3, - ndm[i+1].fst + ndm[i].fst - ndm[i].sec + ndm[i+1].sec);
}
// debug(i);
for(tri cur : transitions[i]){
// debug(cur);
posupd(cur.ff, 0, 0, n-1, cur.sec, INF);
posupd(cur.fs, 0, 0, n-1, cur.sec, manhattan(pts[cur.sec], ndm[i+1]));
}
}
}
Tester's Solution 1
#include <bits/stdc++.h>
using namespace std;
/*
------------------------Input Checker----------------------------------
*/
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
if(!(l <= x && x <= r))
{
cerr << l << ' ' << r << ' ' << x << '\n';
assert(1 == 0);
}
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
/*
------------------------Main code starts here----------------------------------
*/
const int MAX_T = 100000;
const int MAX_N = 1e6+5;
const int MAX_SUM_LEN = 1e5;
#define fast ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define ff first
#define ss second
#define mp make_pair
#define ll long long
#define ii pair<ll,ll>
ll INF = 1e16;
int sum_len = 0;
int max_n = 0;
int yess = 0;
int nos = 0;
int total_ops = 0;
struct segtree{
vector<ii> v;
int sz;
segtree(int n){
v.assign(4*n, mp(INF,0));
sz = 4*n;
}
void relax(int n){
v[n].first += v[n].second;
if(2*n+1 < sz && 2*n+2 < sz){
v[2*n+1].second+=v[n].second;
v[2*n+2].second+=v[n].second;
}
v[n].second = 0;
}
void upd(int n, int l, int r, int pos, ll val){
relax(n);
if(l==r){
v[n] = mp(val,0);
return;
}
int m = (l+r)>>1;
if(pos>m) upd(2*n+2, m+1, r, pos, val);
else upd(2*n+1, l, m, pos, val);
relax(2*n+1);
relax(2*n+2);
v[n].first = min(v[2*n+1].first, v[2*n+2].first);
}
void add(ll val){
if(v[0].first!=INF) v[0].second += val;
}
ll qr(){
relax(0);
return v[0].first;
}
};
int get_quad(ll x, ll y, ll x1, ll y1){
if(x1<=x && y1>=y) return 1;
else if(x1>x && y1<y) return 4;
else if(x1>x && y1>=y) return 2;
return 3;
}
ll get_dis(ll x, ll y, ll x1, ll y1){
return abs(x-x1)+abs(y-y1);
}
int get_sft(vector<vector<ll> > &a, ll val, int f, int n, int qd){
if(!f){
int l=0, r=n-1;
while(l<r){
int m = (l+r)>>1;
if(a[m][0] < val) l=m+1;
else r = m;
}
if(l==n || l==0) l=-1;
return l;
}
else{
int l=0, r=n-1;
while(l<r){
int m = (l+r)>>1;
if(a[m][1] > val) l=m+1;
else r=m;
}
//if(val==3 && f) cout<<l<<"[[[["<<endl;
if(l==n || l==0) l=-1;
//if(val==3 && f) cout<<l<<"[[[["<<endl;
return l;
}
}
void solve()
{
int n,m;
n = readIntSp(1, 1e5);
m = readIntLn(1, 1e5);
vector<ii> pts(n);
vector<vector<ll> > qr(m, vector<ll>(2));
for(int i=0; i<n; i++){
pts[i].ff = readIntSp(-1e9, 1e9);
pts[i].ss = readIntLn(-1e9, 1e9);
}
for(int i=0; i<m; i++){
qr[i][0] = readIntSp(-1e9, 1e9);
qr[i][1] = readIntLn(-1e9, 1e9);
}
segtree s1(n), s2(n), s3(n), s4(n);
vector<vector<int> > q21(m), q31(m), q43(m), q42(m);
for(int i=0; i<n; i++){
int tmp = get_quad(qr[0][0], qr[0][1], pts[i].first, pts[i].second);
ll dis = get_dis(qr[0][0], qr[0][1], pts[i].first, pts[i].second);
switch(tmp){
case 1:{
s1.upd(0, 0, n-1, i, dis);
break;
}
case 2:{
s2.upd(0, 0, n-1, i, dis);
break;
}
case 3:{
s3.upd(0, 0, n-1, i, dis);
break;
}
case 4:{
s4.upd(0, 0, n-1, i, dis);
break;
}
}
int xs = get_sft(qr, pts[i].first, 0, m, tmp);
int ys = get_sft(qr, pts[i].second, 1, m, tmp);
//cout<<xs<<" "<<ys<<endl;
if(xs==-1){
if(ys!=-1){
(tmp==4?q42[ys].push_back(i) : q31[ys].push_back(i));
}
}
else{
if(ys==-1){
if(tmp==4) q43[xs].push_back(i);
else q21[xs].push_back(i);
}
else{
if(xs<=ys){
q43[xs].push_back(i);
q31[ys].push_back(i);
}
else{
q42[ys].push_back(i);
q21[xs].push_back(i);
}
}
}
}
cout<<min({s1.qr(), s2.qr(), s3.qr(), s4.qr()})<<'\n';
//cout<<s1.qr()<<" "<<s2.qr()<<" "<<s3.qr()<<" "<<s4.qr()<<endl;
for(int i=1; i<m; i++){
s1.add(qr[i][0]-qr[i][1]-qr[i-1][0]+qr[i-1][1]);
s2.add(-qr[i][0]-qr[i][1]+qr[i-1][0]+qr[i-1][1]);
s3.add(qr[i][0]+qr[i][1]-qr[i-1][0]-qr[i-1][1]);
s4.add(-qr[i][0]+qr[i][1]+qr[i-1][0]-qr[i-1][1]);
for(auto h:q43[i]){
//cout<<i<<"{"<<h<<endl;
s4.upd(0, 0, n-1, h, INF);
s3.upd(0, 0, n-1, h, get_dis(pts[h].first, pts[h].second, qr[i][0], qr[i][1]));
}
for(auto h:q42[i]){
s4.upd(0, 0, n-1, h, INF);
s2.upd(0, 0, n-1, h, get_dis(pts[h].first, pts[h].second, qr[i][0], qr[i][1]));
}
for(auto h:q21[i]){
s2.upd(0, 0, n-1, h, INF);
s1.upd(0, 0, n-1, h, get_dis(pts[h].first, pts[h].second, qr[i][0], qr[i][1]));
}
for(auto h:q31[i]){
s3.upd(0, 0, n-1, h, INF);
s1.upd(0, 0, n-1, h, get_dis(pts[h].first, pts[h].second, qr[i][0], qr[i][1]));
}
cout<<min({s1.qr(), s2.qr(), s3.qr(), s4.qr()})<<'\n';
//cout<<s1.qr()<<" "<<s2.qr()<<" "<<s3.qr()<<" "<<s4.qr()<<endl;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r" , stdin);
freopen("output.txt", "w" , stdout);
#endif
fast;
int t = 1;
//t = readIntLn(1,MAX_T);
for(int i=1;i<=t;i++)
{
solve();
}
assert(getchar() == -1);
cerr<<"SUCCESS\n";
//cerr<<"Tests : " << t << '\n';
//cerr<<"Sum of lengths : " << sum_len << '\n';
// cerr<<"Maximum length : " << max_n << '\n';
// cerr<<"Total operations : " << total_ops << '\n';
//cerr<<"Answered yes : " << yess << '\n';
//cerr<<"Answered no : " << nos << '\n';
}
Tester's Solution 2
#include <bits/stdc++.h>
using namespace std;
/*
------------------------Input Checker----------------------------------
*/
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
if(!(l <= x && x <= r))
{
cerr << l << ' ' << r << ' ' << x << '\n';
assert(1 == 0);
}
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
/*
------------------------Main code starts here----------------------------------
*/
const int MAX_T = 100000;
const int MAX_N = 100000;
const int MAX_SUM_LEN = 1000000;
#define fast ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define ff first
#define ss second
#define mp make_pair
#define mt make_tuple
#define ll long long
const ll LIM = 1000000000;
#define pll pair<ll ,ll>
#define tll tuple<ll, ll, ll>
int sum_len = 0;
int max_n = 0;
int yess = 0;
int nos = 0;
int total_ops = 0;
ll get_quad(pll a , pll b) // quadrant of b wrt a
{
b.first -= a.first ;
b.second -= a.second ;
if(b.first >= 0 && b.second >= 0)
return 1;
if(b.first >= 0 && b.second < 0)
return 4;
if(b.first < 0 && b.second >= 0)
return 2;
if(b.first < 0 && b.second < 0)
return 3;
return 0;
}
ll get_val(ll quad , pll point)
{
if(quad == 1)
return point.first + point.second ;
if(quad == 2)
return -point.first + point.second ;
if(quad == 3)
return -point.first - point.second ;
if(quad == 4)
return point.first - point.second ;
return 0;
}
void shift(pll prev , pll curr , vector<ll>& current_quad, multiset<ll> vals[], vector<tll> &s_x , vector<tll> &s_y)
{
ll x_ind = lower_bound(s_x.begin() , s_x.end() , mt(prev.first , -LIM , -LIM)) - s_x.begin() ;
while(x_ind < s_x.size() && get<0>(s_x[x_ind]) < curr.first)
{
// cout << "x_ind = " << x_ind << endl ;
pll point;
point.first = get<0>(s_x[x_ind]);
point.second = get<1>(s_x[x_ind]) ;
// cout << "point = (" << point.first << ", " << point.second << ")" << endl ;
ll prev_quad = current_quad[get<2>(s_x[x_ind])];
ll curr_quad = get_quad(curr , point) ;
ll prev_val = get_val(prev_quad , point);
ll curr_val = get_val(curr_quad, point) ;
// cout << "prev_quad = " << prev_quad << " curr_quad = " << curr_quad << endl ;
vals[prev_quad-1].erase(vals[prev_quad-1].find(prev_val)) ;
vals[curr_quad-1].insert(curr_val) ;
current_quad[get<2>(s_x[x_ind])] = curr_quad;
x_ind++ ;
}
ll y_ind = lower_bound(s_y.begin() , s_y.end() , mt(curr.second , -LIM , -LIM)) - s_y.begin() ;
while(y_ind < s_y.size() && get<0>(s_y[y_ind]) < prev.second)
{
pll point;
point.first = get<1>(s_y[y_ind]);
point.second = get<0>(s_y[y_ind]) ;
ll prev_quad = current_quad[get<2>(s_y[y_ind])];
ll curr_quad = get_quad(curr , point) ;
ll prev_val = get_val(prev_quad , point);
ll curr_val = get_val(curr_quad, point) ;
vals[prev_quad-1].erase(vals[prev_quad-1].find(prev_val)) ;
vals[curr_quad-1].insert(curr_val) ;
current_quad[get<2>(s_y[y_ind])] = curr_quad;
y_ind++ ;
}
return ;
}
void solve()
{
ll n , m ;
n = readIntSp(1 , MAX_N);
m = readIntLn(1 , MAX_N) ;
vector<pll> s(n) , t(m) ;
for(ll i = 0 ; i < n ; i++)
{
s[i].first = readIntSp(-LIM, LIM);
s[i].second = readIntLn(-LIM , LIM) ;
}
vector<tll> s_x(n) , s_y(n) ;
for(ll i = 0 ; i < n ; i++)
{
get<0>(s_x[i]) = get<1>(s_y[i]) = s[i].first ;
get<1>(s_x[i]) = get<0>(s_y[i]) = s[i].second ;
get<2>(s_x[i]) = get<2>(s_y[i]) = i ;
}
sort(s_x.begin() , s_x.end()) ;
sort(s_y.begin() , s_y.end()) ;
// cout << "here" << endl ;
for(ll i = 0 ; i < m ; i++)
{
t[i].first = readIntSp(-LIM, LIM);
t[i].second = readIntLn(-LIM , LIM) ;
}
for(ll i = 1 ; i < m ; i++)
{
assert(t[i].first > t[i-1].first) ;
assert(t[i].second < t[i-1].second) ;
}
multiset<ll> vals[4] ;
ll c[4] ;
vector<ll> current_quad(n) ;
for(int i = 0 ; i < n ; i++)
{
current_quad[i] = get_quad(t[0] , s[i]) ;
vals[current_quad[i]-1].insert(get_val(current_quad[i], s[i])) ;
}
// for(int i = 0 ; i < n ; i++)
// {
// cout << current_quad[i] << ' ';
// }
// cout << endl ;
for(ll i = 0 ; i < m ; i++)
{
for(ll j = 0 ; j < 4 ; j++)
c[j] = get_val(j+1 , t[i]) ;
ll mini = (ll)LIM*10;
for(ll j = 0 ; j < 4 ; j++)
{
if(vals[j].size() > 0)
mini = min(mini , *vals[j].begin() - c[j]) ;
}
cout << mini << '\n' ;
if(i != m-1)
{
// cout << "i = " << i << " shifting starts" << endl ;
shift(t[i] , t[i+1] , current_quad , vals , s_x , s_y) ;
// cout << "shifting ends" << endl ;
}
}
return ;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("inputf.txt", "r" , stdin);
freopen("outputf.txt", "w" , stdout);
#endif
fast;
int t = 1;
for(int i=1;i<=t;i++)
{
solve();
}
assert(getchar() == -1);
cerr<<"SUCCESS\n";
cerr<<"Tests : " << t << '\n';
cerr<<"Sum of lengths : " << sum_len << '\n';
// cerr<<"Maximum length : " << max_n << '\n';
// cerr<<"Total operations : " << total_ops << '\n';
//cerr<<"Answered yes : " << yess << '\n';
//cerr<<"Answered no : " << nos << '\n';
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class MINMANH{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni(), M = ni();
long[][] Sx = new long[N][], Sy = new long[N][], T = new long[M][];
for(int i = 0; i< N; i++){
long x = nl(), y = nl();
Sx[i] = new long[]{x, y};
Sy[i] = new long[]{x, y};
}
for(int i = 0; i< M; i++)T[i] = new long[]{nl(), nl()};
Arrays.sort(Sx, (long[] p1, long[] p2) -> Long.compare(p1[0], p2[0]));
Arrays.sort(Sy, (long[] p1, long[] p2) -> Long.compare(p2[1], p1[1]));
// dbg(Sx);
// dbg(Sy);
MyTreeSet<Long>[] P = new MyTreeSet[]{new MyTreeSet<>(), new MyTreeSet<>(), new MyTreeSet<>(), new MyTreeSet<>()};
long[][] D = new long[][]{
{-1,-1},
{-1, 1},
{ 1,-1},
{ 1, 1}
}, Dinv = new long[][]{
{ 1, 1},
{ 1,-1},
{-1, 1},
{-1,-1}
};
for(int i = 0; i< N; i++)P[2].add(eval(D[2], Sx[i]));
long prevX = Integer.MIN_VALUE, prevY = Integer.MAX_VALUE;
for(int i = 0, p1 = 0, p2 = 0; i< M; i++){
//Moving origin from (prevX, prevY) to (T[i][0], T[i][1])
//Moving prigin from (prevX, prevY) to (prevX, T[i][1])
while(p2 < N && Sy[p2][1] >= T[i][1]){
if(Sy[p2][0] <= prevX){
hold(P[0].remove(eval(D[0], Sy[p2])));
P[1].add(eval(D[1], Sy[p2]));
}else{
hold(P[2].remove(eval(D[2], Sy[p2])));
P[3].add(eval(D[3], Sy[p2]));
}
p2++;
}
prevY = T[i][1];
//Moving origin from (prevX, T[i][1]) to (T[i][0], T[i][1])
while(p1 < N && Sx[p1][0] <= T[i][0]){
if(Sx[p1][1] >= prevY){
P[3].remove(eval(D[3], Sx[p1]));
P[1].add(eval(D[1], Sx[p1]));
}else{
P[2].remove(eval(D[2], Sx[p1]));
P[0].add(eval(D[0], Sx[p1]));
}
p1++;
}
prevX = T[i][0];
long ans = Long.MAX_VALUE;
for(int d = 0; d< 4; d++){
if(!P[d].isEmpty()){
ans = Math.min(ans, P[d].first() + eval(Dinv[d], T[i]));
}
}
pn(ans);
}
}
long eval(long[] d, long[] P){
return d[0]*P[0] + d[1]*P[1];
}
//Java Ordered MultiSet, equivalent of c++ multiset<T>
class MyTreeSet<T> implements Iterable<T>{
private int size;
private TreeMap<T, Integer> map;
public MyTreeSet(){
size = 0;
map = new TreeMap<>();
}
public int size(){return size;}
public int dsize(){return map.size();}
public boolean isEmpty(){return size==0;}
public void add(T t){
size++;
map.put(t, map.getOrDefault(t, 0)+1);
}
public boolean remove(T t){
if(!map.containsKey(t))return false;
size--;
int c = map.get(t);
if(c==1)map.remove(t);
else map.put(t, c-1);
return true;
}
public int freq(T t){return map.getOrDefault(t, 0);}
public boolean contains(T t){return map.getOrDefault(t,0)>0;}
public T ceiling(T t){return map.ceilingKey(t);}
public T floor(T t){return map.floorKey(t);}
public T first(){return map.firstKey();}
public T last(){return map.lastKey();}
public Iterator<T> iterator() {
return new MyTreeSetIterator<>(this);
}
class MyTreeSetIterator<T> implements Iterator<T>{
TreeMap<T, Integer> mp;
T element = null;
int cur = 0, freq = 0;
MyTreeSetIterator(MyTreeSet<T> obj){
this.mp = obj.map;
if(!this.mp.isEmpty()){
element = mp.firstKey();
freq = mp.firstEntry().getValue();
}
}
public boolean hasNext(){
return element != null;
}
public T next(){
T ret = element;
cur++;
if(cur == freq){
Map.Entry<T, Integer> e = mp.higherEntry(element);
if(e == null){
element = null;
freq = 0;
}else{
element = e.getKey();
freq = e.getValue();
cur = 0;
}
}
return ret;
}
}
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = false;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new MINMANH().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()