PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Farhod
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Observation
PROBLEM:
There is a hidden array A of length N where N is known. You want to find indices of minimum, second minimum, second maximum and maximum element in the array within \lfloor \frac{3*N}{2} \rfloor +20 queries, where you can ask the following query.
For a query, choose two indices i and j such that 1 \leq i, j \leq N, the grader will compare A_i and A_j and returns i if A_i \leq A_j and returns j otherwise.
QUICK EXPLANATION
- Organize each position from 1 to N as leaves in a binary tree, and for each internal node, assign the position of smaller element among positions of its children.
- This way, the position of smallest element shall be the one stored at the root of the binary tree and the second smallest shall be one of the positions directly compared with the position containing minimum value. There are log_2(N) such positions. Building and finding the minimum takes N-1 queries and finding second minimum takes log_2(N) queries.
- We can repeat the same for maximum, except for noticing that we have already compared first element with second, third with fourth and so on while building tree for minimum, so we reuse the N/2 queries information, leading to \frac{3*N}{2}+2*log_2(N) queries.
EXPLANATION
Let’s forget about the maximum first and focus only on positions of minimum and second minimum value.
Consider a simpler problem, we just need to find the index of the minimum value in an array in N-1 queries.
We can see that we can initially assume the value at position 1 to be minimum, and then consider the next element and compare with the minimum, and updating the index of minimum and so on. We can see that we make exactly N-1 comparisons and in the end, we have an index of the minimum value of whole array.
Consider A = [5, 2, 4, 3]. We initially assume p = 1 such that A_p is minimum. Asking query (1, 2) we get 2 as the position of minimum, so we update p = 2. Now we query (2, 3), we get 2 as the position of minimum, so p remain same. Lastly, we qeury (2, 4) and we get 2 as the position of minimum, so p = 2 is the position containing the minimum value in array A.
Now, what about the second minimum value? One easy approach is to ignore the position of p and run the same process, taking N-2 more queries. We need to do something better, as we have made 2*N-3 queries just for minimum and second minimum.
An important observation about second minimum is that during the first pass, the second minimum element must be compared with the minimum element. It can be easily proved intuitively.
Now, let us make the list of positions, which were compared with position p during the first pass. Let S be the size of this list. Our required second minimum can be found by a single pass in this list, taking S-1 queries. In our current approach, S can go up to N-1 in case the A_1 or A_2 is the minimum value.
Now, we do not know before asking queries, but we somehow want to minimize S without knowing the final position of the minimum. The idea is to minimize S for all positions.
Now, instead of asking queries from left to right, let’s ask queries differently.
Compare first element with the second, third element with the fourth, fifth element with sixth and so on. We got N/2 positions and we know, that the minimum position is one of these. Repeating the same process, we compare the first position with the second, third with the fourth and so on. Assume N to be a power of 2 for simplicity.
The queries form a binary tree-like structure, as follows for N = 4.
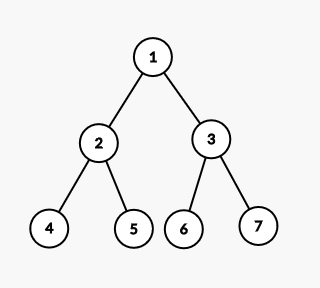
In the above tree, Node 4 to Node 7 contains positions 1 to 4. Node 2 stores the position of the minimum of A_1 and A_2, Node 3 stores the position of minimum among A_3 and A_4 and finally, at Node 1, the positions stores in node 2 and 3 are queried and the position containing minimum is taken. The position stored at Node 1 is the position of minimum value.
Now, we can see that the final winner is compared at most log_2(N) times with some other position (once at each depth of the binary tree). So, we have restricted the size of list to log_2(N) which, for N \leq 1024 is 10. Hence, by running the linear pass on these 10 positions, we have managed to find the positions of minimum and second minimum in N-1+(10-1) = N+8 queries.
Now, If we repeat the same process for maximum, we can solve the problem in 2*N+16 queries, which will get 50 points, but for the last 50 points, one crucial observation is left.
When repeating the process for the position of maximum value, we can see that we have already queried the minimum of first and second position, third and fourth position. So, we can reuse the results of those queries to get first N/2 winners for maximum, saving N/2 queries. So, the total number of queries becomes \displaystyle\frac{3*N}{2}+16 which is sufficient to solve the problem.
There may exist any other approach, so feel free to share how you solved it.
TIME COMPLEXITY
The time complexity is O(N) or O(N*log_2(N)) per test case, depending upon implementation.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
#define fi first
#define se second
const int N = 1010;
using namespace std;
int n;
vector < int > can[N];
int ask(int x, int y)
{
cout << 1 << " " << x << " " << y << endl;
int res;
cin >> res;
return res;
}
int build(int l, int r, vector < int > A, bool for_min)
{
if(l == r){
return A[l];
}
int m = (l + r) / 2;
int x = build(l, m, A, for_min), y = build(m + 1, r, A, for_min);
int need = ask(x, y), op = x ^ y ^ need;
if(for_min == false){
swap(need, op);
}
can[need].push_back(op);
return need;
}
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++){
can[i].clear();
}
vector < int > A, B;
for(int i = 1; i + 1 <= n; i += 2){
int j = ask(i, i + 1), h = i ^ (i + 1) ^ j;
A.push_back(j);
B.push_back(h);
can[j].push_back(h);
can[h].push_back(j);
}
if(n & 1){
A.push_back(n);
B.push_back(n);
}
int min_1 = build(0, (int)A.size() - 1, A, true);
int max_1 = build(0, (int)B.size() - 1, B, false);
int min_2 = -1, max_2 = -1;
for(int x: can[min_1]){
if(min_2 == -1 || ask(x, min_2) == x){
min_2 = x;
}
}
for(int x: can[max_1]){
if(max_2 == -1 || ask(x, max_2) == max_2){
max_2 = x;
}
}
cout << 2 << " " << min_1 << " " << min_2 << " " << max_2 << " " << max_1 << endl;
}
int main()
{
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
ios_base::sync_with_stdio(0);
int T = 1;
cin >> T;
while(T--){
solve();
}
}
Tester's Solution
//teja349
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
//setbase - cout << setbase (16); cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 << endl; prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
using namespace __gnu_pbds;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
#define flush fflush(stdout)
#define primeDEN 727999983
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// find_by_order() // order_of_key
typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;
vector<vi> adj(123);
int ask(int i,int j){
i++;
j++;
cout<<1<<" "<<i<<" "<<j<<endl;
int val;
cin>>val;
return val-1;
}
int buildmintree(int n){
int i;
adj[0].clear();
rep(i,n){
adj[0].pb(i);
}
i=0;
while(adj[i].size()>1){
adj[i+1].clear();
int j=0;
while(j<adj[i].size()){
if(j+1==adj[i].size())
adj[i+1].pb(adj[i][j]);
else
adj[i+1].pb(ask(adj[i][j],adj[i][j+1]));
j+=2;
}
i++;
}
return i;
}
int buildmaxtree(int n){
int i;
for(i=0;i<n;i+=2){
if(i+1==n)
continue;
if(adj[0][i]==adj[1][i/2]){
adj[1][i/2]=adj[0][i+1];
}
else{
adj[1][i/2]=adj[0][i];
}
}
i=1;
while(adj[i].size()>1){
adj[i+1].clear();
int j=0;
while(j<adj[i].size()){
if(j+1==adj[i].size())
adj[i+1].pb(adj[i][j]);
else{
int vali=ask(adj[i][j],adj[i][j+1]);
if(vali==adj[i][j])
vali=adj[i][j+1];
else
vali=adj[i][j];
adj[i+1].pb(vali);
}
j+=2;
}
i++;
}
return i;
}
vi vec;
int getpossible(int val){
int ans=adj[val][0];
int pos=0;
int i;
fd(i,val-1,0){
//cout<<val-1<<" "<<pos<<endl;
if(2*pos+1==adj[i].size()){
pos*=2;
continue;
}
if(adj[i][2*pos]==ans){
vec.pb(adj[i][2*pos+1]);
pos*=2;
}
else{
vec.pb(adj[i][2*pos]);
pos=2*pos+1;
}
}
return 0;
}
int main(){
std::ios::sync_with_stdio(false); cin.tie(NULL);
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int val=buildmintree(n);
int a=adj[val][0];
vec.clear();
getpossible(val);
int b=vec[0];
int i;
f(i,1,vec.size()){
b=ask(b,vec[i]);
}
val=buildmaxtree(n);
vec.clear();
int d=adj[val][0];
getpossible(val);
int c=vec[0],vali;
f(i,1,vec.size()){
vali=ask(c,vec[i]);
if(vali==c){
c=vec[i];
}
}
cout<<2<<" "<<a+1<<" "<<b+1<<" "<<c+1<<" "<<d+1<<endl;
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
class MINMAXIN{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
TreeMap<Query, Integer> q = new TreeMap<>();
int n = ni();
int m = 1;
while(m<n)m<<=1;
int[] t = new int[m<<1];
Arrays.fill(t, -1);
// Building Tree for minimum, -1 denote a ficticious leaf
for(int i = 0; i< n; i++)t[i+m] = i;
for(int i = m-1; i> 0; i--)t[i] = min(q, t[i<<1], t[i<<1|1]);
int a = t[1];//root, containing position of minimum
int[] ar = new int[11];int cnt = 0;
int cur = a+m;//leaf containing minimum
while(cur > 1){
//position stored at cur^1 is compared with position stored at cur
if(t[cur^1] != -1)ar[cnt++] = t[cur^1];
cur>>=1;
}
hold(cnt <= 10);
int b = ar[0];
for(int i = 1; i< cnt; i++)b = min(q, b, ar[i]);
//Repeating same process for maximum
Arrays.fill(t, -1);
for(int i = 0; i< n; i++)t[i+m] = i;
for(int i = m-1; i> 0; i--)t[i] = max(q, t[i<<1], t[i<<1|1]);
int d = t[1];
cur = t[1]+m;
cnt = 0;
while(cur > 1){
if(t[cur^1] != -1)ar[cnt++] = t[cur^1];
cur>>=1;
}
int c = ar[0];
for(int i = 1; i< cnt; i++)c = max(q, c, ar[i]);
a++;b++;c++;d++;
pni(2 +" "+a+" "+b+" "+c+" "+d);
}
int min(TreeMap<Query, Integer> q, int i, int j) throws Exception{
if(Math.min(i, j) == -1)return Math.max(i, j);
Query qq = new Query(i, j);
if(q.containsKey(qq))return q.get(qq);
pni(1+" "+(1+qq.i)+" "+(1+qq.j));
q.put(qq, ni()-1);
return q.get(qq);
}
int max(TreeMap<Query, Integer> q, int i, int j) throws Exception{
if(Math.min(i, j) == -1)return Math.max(i, j);
return i^j^min(q, i, j);
}
class Query implements Comparable<Query>{
int i, j;
public Query(int I, int J){i = Math.min(I, J);j = Math.max(I, J);}
public int compareTo(Query q){if(i != q.i)return Integer.compare(i, q.i);return Integer.compare(j, q.j);}
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
DecimalFormat df = new DecimalFormat("0.00000000000");
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new MINMAXIN().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()