Editorial (unofficial) for Multiplication Program (MULDIG)
PROBLEM LINK:
First of all – it is an excellent problem. Thanks to the author. I really enjoyed it.
PROBLEM:
The problem definition looks simple:
Bear Limak hopes you can solve the following problem. You are given an integer Bwhich is equal to 3, 5 or 7. Your goal will be to print a sequence of moves that are able to multiply any two 2-digit numbers X and Y in base B.
Consider a computer memory consisting of 105 cells, numbered 0 through 105-1, each storing one digit (in base B, a digit must be between 0 and B - 1, inclusive). Let ti denote the digit in the i-th cell. Initially:
• ti = i for i < B
• tB and tB+1 are digits of the number X, so X = tB * B + tB+1
• tB+2 and tB+3 are digits of the number Y, so Y = tB+2 * B + tB+3
• ti = 0 for all i > B+3
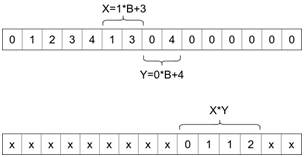
The first of the two drawings above shows the initial situation for B = 5 and multiplying numbers 8 and 4 (represented in base 5 as 13 and 04 respectively). After applying your sequence of moves, the result of the multiplication should be stored in cells B+4, B+5, B+6, B+7, which is shown in the second drawing (please note that 8 * 4 = 32 and this number is represented as 0112 in base 5). Except for those 4 cells containing the answer, the final value of ti doesn’t matter. In particular, you are allowed to change values in the first B+4 cells.
You should choose one function F : [0,B-1] × [0,B-1] → [0,B-1]. It means that the function F should take two digits and return one, where each digit is in the set {0, 1, …, B-1}. One example of F is addition F(x, y) = (x + y) % B. We don’t require any particular properties from F (e.g. associativity or symmetricity).
You should create a sequence of at most 10^5 moves. In each move, choose three cells c1, c2 and c3, not necessarily distinct. The result of F for digits in cells c1 and c2 will be computed, and then written in the cell c3. In other words, in C++ or Python it’s the operation t[c3] = F(t[c1], t[c2]). For every possible pair of 2-digit numbers X and Y, your sequence of moves should produce the correct answer X * Y as described above.
EXPLANATION:
First thing that jumps to mind – Turing machine, second – hardware multiplication schema. But after thinking a bit I’ve realised it is not so simple. In Turing machine we don’t have the limitation for a single function. Second though is a bit more useful. Let’s start with hardware multiplication. It requires “multiply” and “add” functions to perform proper multiplication of 2 digit numbers (the base actually doesn’t matter). There are many ways to do it, but most straightforward is the following way.
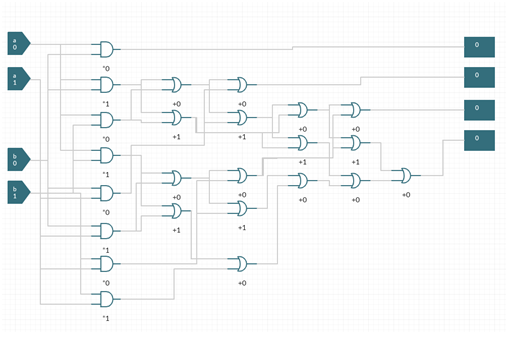
The multiplication is pretty much like multiplication of the numbers on paper. First column multiplies numbers a0 x b0, a0 x b1, b0 x a1, b1 x a1 , then the following columns just add them in the right order including all carry-over values that generated from adding two numbers (that is why you need 10 adders. In fact every pair (x0 x1) can be presented as one element with two inputs and two outputs (remember multiplication of two single digit numbers produces two digit number, the same true for addition). But it may be easier to present it like above to highlight that the logical function table for first and second digits are different.
So what are these functions? (for base 3)
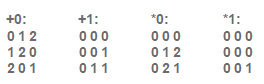
“x0” – means first digit of multiplication of a x b,
“+1” means second digit of addition a + b.
That means if you multiply 2 x 2 – the first digit of the result is 1 and the second is 1 (which gives you 1 x 3+1 =4)
Now here is the problem. There are 4 functions and we can use only one! (I’ve stuck for half a day thinking how that can be done. Of course there is a solution. In fact this problem can be solved in many ways.)
So, we will need only one simple function which works like following:
Function:
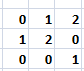
What exactly that means:
if a is 0 - then result is b without change
if a is 1 – the result is b+1
if a is 2 – then result is 1 only if b is 2. and 0 otherwise.
Using only these three “operations” we can do everything, in fact for base 5, 7, (and any other) we don’t need any other “operations” for additional values of “a”. (Yes of course we can use them to speed up/simplify the logic. i.e. to increment by 2 , increment by 3 etc… but in fact it is not required as increment by 2 can be modelled as 2 increments by 1.
So how we going to create 4 functions from above using the function “F”.
First of all lets create operational field. We will have “accumulator” or temporary element “t”. Rectangular field BxB – call it O[B][B], and two fields of the results. R0,R1. (we will use two fields as we going to do x0 and x1 pair of functions at once (the same for +0, +1)
The trick is simple. Imagine “a” is 0 – how many times we need to add 1 to it to make it two? – two time. Brilliant, so we feed F(1,a)->t, F(1,t)->t. Now, if a was zero then t will contain 2. Lets convert it to 1, F(2,t)->t , now if “a” was 0 – then t contains 1.
Now let’s use this 1 as function to mark row on operational field:
for (int i = 0; i<Base; ++i) { F(t,O[0][i])-> O[0][i];}
Think about it carefully. Imagine O[B][B] as a square (initially all set to 0)- if “a” was 0 – then now the 0th row of O[B][B] will contain all 1s while everything else still 0.
Equally if “a” was not zero – then O[B][B] would not change at all as F(0,x) produces the same x
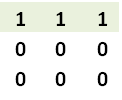
Now we will repeat the same for possible value “1” , obviously in this case we only need to increment once to get the value to 2.
F(1,a)->t
F(2,t)->t
for (int i = 0; i<Base; ++i) { F(t,O[1][i])-> O[1][i]; }
Now if “a” was 1 – then the 1st row of the field will have 1s.
Now for value “2”:
F(2,a)->t
for (int i = 0; i<Base; ++i) { F(t,O[2][i])-> O[2][i]; }
Now lets deal with “b”,
We do almost the same but now we affect columns rather than rows!
F(1,b)->t
F(1,t)->t
F(2,t)->t
for (int i = 0; i<Base; ++i) { F(t,O[i][0]) -> O[i][0]; }
and the same for possible values 1, and 2.
(In fact that all nicely wraps into cycle from 0 to B, so the code is actually very compact.
So what has happened now – the increment of the columns put 1s into the column corresponding to the value of “b”, but wait a second it is increment, that means the value that was in the row produced for “a” that sits in the same column as value for “b” was now incremented from 1 to 2. Bingo! We have got row of ones for the value of “a” column of 1s for the value of “b” and on intersection of these values we have got 2.
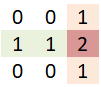
Lets clean the 1s and convert 2 into 1,
for(int i=0; i<B; ++i) {
for(int j=0; j<B; ++j) {
F(2,O[i][j])->O[i][j];
}
}
Now the whole field is empty except one cell corresponding to the values a and b (if a was 1 and b was 2 – then cell O[1][8] will have 1 and everywhere else it will be 0.
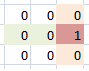
Now we can implement functions we needed.
If we look for the function “x0” and “x1” (they will be formed in results R0 R1)
For each cell in the field O[a][b] we know exactly what we should get!
If it is 0 – we don’t need to do anything
If it is 1 – we need to increment it once.
If it is 2 – we need to increment it twice!
for(int i=0;i<B;++i) {
for(int j=0;j<B;++j) {
for(int k=0; k< Ft_mul_0[i][j];++k) {
F(O[i][j],R0)->R0;
}
for(int k=0; k< Ft_mul_1[i][j];++k) {
F(O[i][j],R1)->R1;
}
}
}
Remember we do it for every cell but cells that have “0” in them – don’t affect the result and the only cell that works – is the one that has “1” in it!
Obviously the same is done for the functions “+0, and +1”
We’ve got it!
In fact we can reuse the same t, O[B][B], R0,R1 if we just move result values R0,R1 to other memory location and clean up all the working area (F(0,0) – always produces 0).
The rest is simple.
Remember the schema at the beginning? We are going to build exactly it!
You need about 20 intermediate variables (roughly corresponding to all internal connections in the schema:
int addrA1 = B + 0;
int addrA0 = B + 1;
int addrB1 = B + 2;
int addrB0 = B + 3;
int addrC3 = B + 4;
int addrC2 = B + 5;
int addrC1 = B + 6;
int addrC0 = B + 7;
int addrR0 = B + 8 + B*B + 1;
int addrR1 = B + 8 + B*B + 2;
// intermediate variables
int addrAB = 100; //- there will be 8 of them this is just beginning of the array
int addrAB1 = 110; // the variables roughly correspond to the columns on the H/W multiplication schema
int addrAB2 = 120;
int addrAB3 = 130;
int addrAB4 = 140;
int addrAB5 = 150;
Remember you always can move the value as F(0,src)->dst
This code below doesn’t change for different Base B.
calc_mul01(B, addrA0, addrB0, R); // multiplies addrA0 and addrB0 , the result is always in R0,R1
cmove(B, addrR0, addrAB + 0, R);
cmove(B, addrR1, addrAB + 1, R);
calc_mul01(B, addrA0, addrB1, R);
cmove(B, addrR0, addrAB + 2, R);
cmove(B, addrR1, addrAB + 3, R);
calc_mul01(B, addrA1, addrB0, R);
cmove(B, addrR0, addrAB + 4, R);
cmove(B, addrR1, addrAB + 5, R);
calc_mul01(B, addrA1, addrB1, R);
cmove(B, addrR0, addrAB + 6, R);
cmove(B, addrR1, addrAB + 7, R);
cmove(B, addrAB + 0, addrC0, R); // c0 <- at this point we produce lowest digit of the result
calc_add01(B, addrAB + 1, addrAB + 2, R); // adds addrAB[1] and addrAB[2] , the result is always in R0,R1
cmove(B, addrR0, addrAB1 + 0, R);
cmove(B, addrR1, addrAB1 + 1, R);
calc_add01(B, addrAB + 3, addrAB + 5, R);
cmove(B, addrR0, addrAB1 + 2, R);
cmove(B, addrR1, addrAB1 + 3, R);
calc_add01(B, addrAB1 + 0, addrAB + 4, R);
cmove(B, addrR0, addrAB2 + 0, R);
cmove(B, addrR1, addrAB2 + 1, R);
calc_add01(B, addrAB1 + 2, addrAB + 6, R);
cmove(B, addrR0, addrAB2 + 2, R);
cmove(B, addrR1, addrAB2 + 3, R);
calc_add01(B, addrAB1 + 3, addrAB + 7, R);
cmove(B, addrR0, addrAB2 + 4, R);
cmove(B, addrAB2 + 0, addrC1, R); // c1 <- at this point we produced second digit of the result.
calc_add01(B, addrAB2 + 1, addrAB1 + 1, R);
cmove(B, addrR0, addrAB3 + 0, R);
cmove(B, addrR1, addrAB3 + 1, R);
calc_add01(B, addrAB2 + 3, addrAB2 + 4, R);
cmove(B, addrR0, addrAB3 + 2, R);
calc_add01(B, addrAB3 + 0, addrAB2 + 2, R);
cmove(B, addrR0, addrAB4 + 0, R);
cmove(B, addrR1, addrAB4 + 1, R);
calc_add01(B, addrAB3 + 1, addrAB3 + 2, R);
cmove(B, addrR0, addrAB4 + 2, R);
cmove(B, addrAB4 + 0, addrC2, R); // c2 <- third digit
calc_add01(B, addrAB4 + 1, addrAB4 + 2, R);
cmove(B, addrR0, addrAB5 + 0, R);
cmove(B, addrAB5 + 0, addrC3, R); // c3 <- fourth digit. We are done!
Now the only thing left – is to print the correctly formatted output.
The solution requires only very small adjustment for different base, and in fact the part above doesn’t change at all.
CONCLUSION:
You only need: Acc 1, OpField BxB, Result 2, and ~20 temporary variables (actually 5-6 would be enough).
i.e. for Base 3 => we need 32 memory cells
Base 5 => we need 48 cells
Base 7 => we need 72 cells
It makes more steps, but who cares? You need 890 commands for base 3, 2636 for base 5 and just over 5962 for base 7, In fact using the constrains (100000 cells and steps you could produce machine for multiplication of many digits and in much higher base, especially if some optimization (+2,+3,etc…) is used for higher B.
See the corresponding solution: https://www.codechef.com/viewsolution/14508220