PROBLEM LINK:
Author: Sachin Yadav
Tester: Taranpreet Singh
Editorialist: N.V. Karthikeya
DIFFICULTY:
EASY
PREREQUISITES:
Precomputation, Prefix-Sums
PROBLEM:
Given a square matrix of integers find the maximum value which can be obtained by adding all the elements in a diamond in that matrix. Refer the figure given in the problem for a better idea.
QUICK EXPLANATION:
Key observation here would be that given a cell as center , for getting the sum of diamond of larger size, we only need to add diagonal boundary cells to a smaller diamond
Precompute the prefix-sums of all the diagonals from left-top to right-bottom as well as left-bottom to right-top.
Now iterate over all the cells of the matrix, in each iteration consider that cell to be the centre of the diamond and find the maximum valued diamond corresponding to that cell using the calculated prefix sums of diagonals.
So once we find the maximum corresponding to each centre the maximum value possible is maximum amongst all these calculated values.
EXPLANATION:
Precomputation :
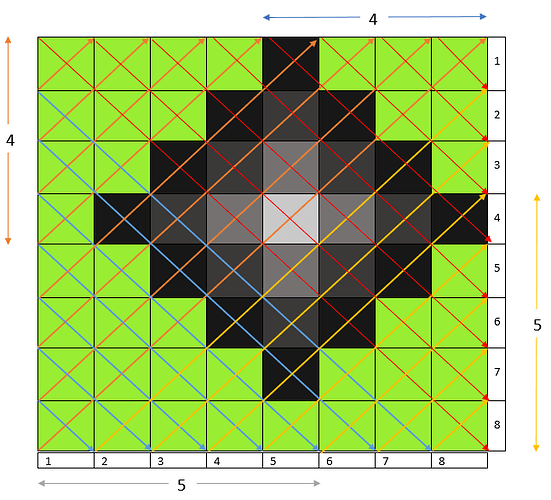
We need to find prefix-sums corresponding to all the diagonals from top-left to bottom-right as well as bottom-left to top-right as shown in the figure. There are 2\times N-1 first kind of diagonals and 2\times N-1 second kind of diagonals, so totally there are 4\times N-2 diagonals.
Let us maintain four N \times N matrices for easy understanding and let each of these represent the diagonals corresponding to the upper half triangle and lower half triangles. So precomp1_upper, precomp1_lower, precomp2_upper and precomp2_lower corresponding to red, blue, orange and yellow colours in the figure respectively.
Now precomp1_upper[i][j] represents diagonal starting at cell matrix[1][i] and having length j. So starting with length one we can compute prefix sums of this matrix in O(N^2), similarily precompute for the remaining 3 matrices.
Now as mentioned in the quick explanation iterate over each cell of the given matrix by considering matrix[i][j] as centre in each iteration and now find maximum value diamond corresponding to that centre.
Now to compute for the cell matrix[4][5] in the figure, we initially can figure out the maximum size of diamond possible as min(i,j,N-i+1,N-j+1)-1. We start the 0 size diamond which is just the centre so compare the maximum till now with cell value and update maximum also assign this value calculated to a variable.
value[diamond of size 2]=value[diamond of size 1] + [(precomp1_upper[3][4] - precomp1_upper[3][2]) + (precomp1_upper[1][5] - precomp1_upper[1][3]) + (precomp2_upper[7][5] - precomp2_upper[7][3]) + (precomp2_lower[2][5] - precomp2_lower[2][3])] - [matrix[5][3] + matrix[6][4] + matrix[5][5] + matrix[4][4]].
We basically added the surrounding 4 diagonals and subracted the common corners once, as we have added them twice while adding diagonals. Similarily do this for all sizes and all possible centres.
TIME COMPLEXITY:
- O(N^3)
SOLUTIONS:
Setter's Solution
#include<iostream>
typedef long long ll;
using namespace std;
int T, N;
int arr[101][101];
ll dig1[205][202]={0}, dig2[205][202]={0};
pair<int,int> dig1_idx(pair<int,int> pt)
{
pair<int,int> res;
if(pt.first>=pt.second)
return {N-1-(pt.first-pt.second),pt.second};
else return {N-1 + pt.second-pt.first,pt.first};
}
pair<int,int> dig2_idx(pair<int,int> pt)
{
if(N-1-pt.first<=pt.second) return {2*N -2 - pt.first - pt.second,N-1-pt.second};
else return {2*N -2 - pt.first - pt.second,pt.first};
}
void compute_diagnols()
{
int dig1_cnt=0;
for(int i=N-1; i>=0; i--)
{
for(int j=0; j<N-i; j++)
dig1[dig1_cnt][j+1]=arr[i+j][j]+ dig1[dig1_cnt][j];
dig1_cnt++;
}
for(int j=1; j<N; j++)
{
for(int i=0; i<N-j; i++)
dig1[dig1_cnt][i+1]=arr[i][i+j] + dig1[dig1_cnt][i];
dig1_cnt++;
}
int dig2_cnt=0;
for(int i=N-1; i>=0; i--)
{
for(int j=0; j<N-i; j++)
dig2[dig2_cnt][j+1]=arr[i+j][N-1-j]+dig2[dig2_cnt][j];
dig2_cnt++;
}
for(int j=N-2; j>=0; j--)
{
for(int i=0; i<=j; i++)
dig2[dig2_cnt][i+1]=arr[i][j-i]+dig2[dig2_cnt][i];
dig2_cnt++;
}
}
ll solve()
{
compute_diagnols();
ll answer=arr[0][0];
ll temp;
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
{
ll temp=arr[i][j];
answer=max(answer,temp);
int max_side=min(min(i,j),min(N-i-1,N-j-1));
for(int side=1; side<=max_side; side++)
{
pair<int,int> l={i,j-side}, r={i,j+side};
pair<int,int> t={i-side,j}, b={i+side, j};
temp+=arr[l.first][l.second]+arr[r.first][r.second]+arr[t.first][t.second] + arr[b.first][b.second];
pair<int,int> dig1_b=dig1_idx(b), dig1_r=dig1_idx(r);
pair<int,int> dig2_b=dig2_idx(b), dig2_l=dig2_idx(l);
temp+=dig1[dig1_b.first][dig1_b.second]+dig1[dig1_r.first][dig1_r.second]+ dig2[dig2_b.first][dig2_b.second]+ dig2[dig2_l.first][dig2_l.second];
temp-=dig1[dig1_b.first][dig1_b.second-side+1]+dig1[dig1_r.first][dig1_r.second-side+1]+ dig2[dig2_b.first][dig2_b.second-side+1]+ dig2[dig2_l.first][dig2_l.second-side+1];
answer=max(temp,answer);
}
}
return answer;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> T;
while(T--)
{
cin>>N;
for(int i =0; i<N; i++) for(int j=0; j<N; j++) cin>>arr[i][j];
cout<<solve()<<"\n";
}
return 0;
}
Tester's Solution
import java.util.*;
import java.io.*;
import java.text.*;
public class Main{
//SOLUTION BEGIN
//Into the Hardware Mode
void pre() throws Exception{}
void solve(int TC)throws Exception{
int n = ni();
long[][] g = new long[2+n][2+n];
for(int i = 1; i<= n; i++)
for(int j = 1; j<= n; j++)
g[i][j] = nl();
long[][] d1 = new long[2+n][2+n], d2 = new long[2+n][2+n];
for(int i = 1; i<= n; i++){
for(int j = 1; j<= n; j++){
d1[i][j] = d1[i-1][j-1]+g[i][j];
d2[i][j] = d2[i-1][j+1]+g[i][j];
}
}
long ans = -IINF;
for(int i = 1; i<= n; i++){
for(int j = 1; j<= n; j++){
long cur = g[i][j];
ans = Math.max(ans, cur);
for(int d = 1; Math.max(i, j)+d <= n && Math.min(i, j) > d; d++){
cur += d1[i-1][j+d-1]-d1[i-d][j];
cur += d1[i+d-1][j-1]-d1[i][j-d];
cur += d2[i-1][j-d+1]-d2[i-d][j];
cur += d2[i+d-1][j+1]-d2[i][j+d];
cur += g[i][j+d]+g[i][j-d]+g[i-d][j]+g[i+d][j];
ans = Math.max(ans, cur);
}
}
}
pn(ans);
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
void exit(boolean b){if(!b)System.exit(0);}
long IINF = (long)1e18, mod = (long)1e9+7;
final int INF = (int)1e9, MX = (int)2e6+5;
DecimalFormat df = new DecimalFormat("0.0000000");
double PI = 3.141592653589793238462643383279502884197169399, eps = 1e-7;
static boolean multipleTC = true, memory = false, fileIO = false;
FastReader in;PrintWriter out;
void run() throws Exception{
if(fileIO){
in = new FastReader("C:/users/user/desktop/inp.in");
out = new PrintWriter("C:/users/user/desktop/out.out");
}else {
in = new FastReader();
out = new PrintWriter(System.out);
}
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();
for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
if(memory)new Thread(null, new Runnable() {public void run(){try{new Main().run();}catch(Exception e){e.printStackTrace();}}}, "1", 1 << 28).start();
else new Main().run();
}
int find(int[] set, int u){return set[u] = (set[u] == u?u:find(set, set[u]));}
int digit(long s){int ans = 0;while(s>0){s/=10;ans++;}return ans;}
long gcd(long a, long b){return (b==0)?a:gcd(b,a%b);}
int gcd(int a, int b){return (b==0)?a:gcd(b,a%b);}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}