PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: Utkarsh Gupta, Jeevan Jyot Singh
Testers: Abhinav Sharma, Venkata Nikhil Medam
Editorialist: Nishank Suresh
DIFFICULTY:
1745
PREREQUISITES:
Prefix sums
PROBLEM:
Chef has a binary string A of length N. He creates binary string B by concatenating M copies of A. Find the number of positions in B such that pref_i = suf_{i+1}.
EXPLANATION:
Let S denote the sum of A, i.e, S = A_1 + A_2 + \ldots + A_N.
Now, suppose we know that pref_i = suf_{i+1} for some index i of B. What can we say about pref_i?
Answer
pref_i must be equal to \frac{M\cdot S}{2}.
This is because pref_i + suf_{i+1} always equals the total sum of B, which is M\cdot S (since B is formed from M copies of A).
Note that the above division is not floor division. In particular, when M\cdot S is odd, no good index can exist.
Now the problem reduces to finding the number of indices of B whose prefix sum is a given value. This can be done in several ways, though they all depend on the fact that the prefix sums are non-decreasing. For example:
- Since M is small, it is possible to simply iterate over the number of copies while the current prefix sum is smaller than the target value, each time adding S to the current prefix sum. When the prefix sum exceeds the target, iterate across that copy of A in \mathcal{O}(N) and count the number of good indices. This takes \mathcal{O}(N + M) time.
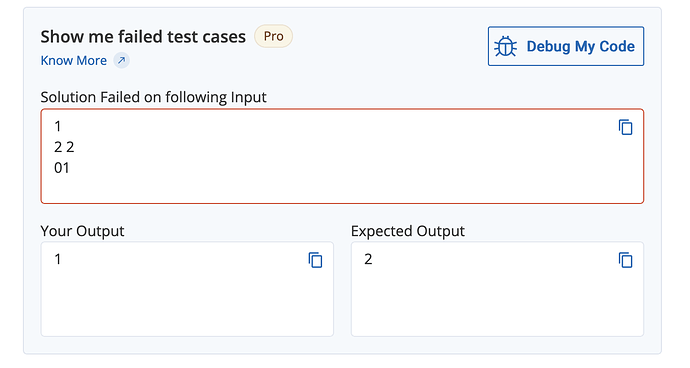
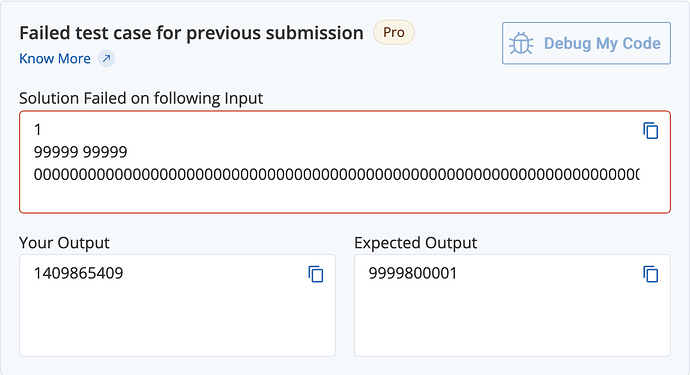
- Some care needs to be taken when implementing this. For example, it might be that the next copy of A (if it exists) also contributes some indices to the answer, for example if A starts with a 0. Also, depending on implementation, a string with all zeros might be an edge case for the solution, causing either TLE or WA since all N\cdot M indices are good.
- Another option with less thinking involved is to binary search for the first and last positions with the target prefix sum. The prefix sum for a given position can be calculated in \mathcal{O}(1) if we know the prefix sums of A, and so this solution runs in \mathcal{O}(\log(N\cdot M)). It still requires \mathcal{O}(N) time to read the input string, however.
TIME COMPLEXITY:
\mathcal{O}(N + M) or \mathcal{O}(N + \log(N\cdot M)) per test case, depending on implementation.
CODE:
Setter (C++)
#ifdef WTSH
#include <wtsh.h>
#else
#include <bits/stdc++.h>
using namespace std;
#define dbg(...)
#endif
#define int long long
#define endl "\n"
#define sz(w) (int)(w.size())
using pii = pair<int, int>;
const int mod = 998244353;
// -------------------- Input Checker Start --------------------
long long readInt(long long l, long long r, char endd)
{
long long x = 0;
int cnt = 0, fi = -1;
bool is_neg = false;
while(true)
{
char g = getchar();
if(g == '-')
{
assert(fi == -1);
is_neg = true;
continue;
}
if('0' <= g && g <= '9')
{
x *= 10;
x += g - '0';
if(cnt == 0)
fi = g - '0';
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if(g == endd)
{
if(is_neg)
x = -x;
if(!(l <= x && x <= r))
{
cerr << "L: " << l << ", R: " << r << ", Value Found: " << x << '\n';
assert(false);
}
return x;
}
else
{
assert(false);
}
}
}
string readString(int l, int r, char endd)
{
string ret = "";
int cnt = 0;
while(true)
{
char g = getchar();
assert(g != -1);
if(g == endd)
break;
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) { return readInt(l, r, ' '); }
long long readIntLn(long long l, long long r) { return readInt(l, r, '\n'); }
string readStringSp(int l, int r) { return readString(l, r, ' '); }
string readStringLn(int l, int r) { return readString(l, r, '\n'); }
void readEOF() { assert(getchar() == EOF); }
vector<int> readVectorInt(int n, long long l, long long r)
{
vector<int> a(n);
for(int i = 0; i < n - 1; i++)
a[i] = readIntSp(l, r);
a[n - 1] = readIntLn(l, r);
return a;
}
// -------------------- Input Checker End --------------------
int sumN = 0;
void solve()
{
int n = readIntSp(1, 1e5);
sumN += n;
int m = readIntLn(1, 1e5);
string a = readStringLn(n, n);
assert(*min_element(a.begin(), a.end()) >= '0' and *max_element(a.begin(), a.end()) <= '1');
int S = count(a.begin(), a.end(), '1');
if(S == 0)
cout << n * m << endl;
else if(S * m % 2 == 1)
cout << 0 << endl;
else
{
string b = a;
if(m % 2 == 0)
b += a, S += S;
int cur = 0, ans = 0;
for(int i = 0; i < sz(b); i++)
{
cur += b[i] - '0';
if(2 * cur == S)
ans++;
}
cout << ans << endl;
}
}
int32_t main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int T = readIntLn(1, 1e5);
for(int tc = 1; tc <= T; tc++)
{
// cout << "Case #" << tc << ": ";
solve();
}
readEOF();
assert(sumN <= 2e5);
return 0;
}
Tester (C++)
// Tester: Nikhil_Medam
#include <bits/stdc++.h>
#pragma GCC optimize ("-O3")
using namespace std;
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
#define int long long
#define double long double
const int N = 1e5 + 5;
int t, n, m;
string s;
int32_t main() {
cin >> t;
while(t--) {
cin >> n >> m >> s;
int sum = 0;
for(int i = 0; i < n; i++) {
sum += (s[i] - '0');
}
if(sum == 0) {
cout << n * m << endl;
}
else if ((sum * m) % 2 == 1) {
cout << 0 << endl;
}
else {
if(m % 2 == 0) {
int cnt_0_start = 0, cnt_0_end = 0;
for(int i = 0; i < n; i++) {
if(s[i] == '1') {
break;
}
cnt_0_start++;
}
for(int i = n - 1; i >= 0; i--) {
if(s[i] == '1') {
break;
}
cnt_0_end++;
}
cout << cnt_0_start + cnt_0_end + 1 << endl;
}
else {
int ans = 0, cur_sum = 0;
for(int i = 0; i < n; i++) {
cur_sum += (s[i] - '0');
ans += (cur_sum == sum / 2);
if(cur_sum > sum / 2) {
break;
}
}
cout << ans << endl;
}
}
}
return 0;
}
Editorialist (Python)
for _ in range(int(input())):
n, m = map(int, input().split())
s = input()
# pref[i] = suf[i+1]
# pref[i] + suf[i+1] = S
# pref[i] = S/2
tot = s.count('1')
target = tot*m
if target%2 == 1:
print(0)
continue
if target == 0:
print(n*m)
continue
target //= 2
cur = 0
while m > 0:
if cur + tot < target:
m -= 1
cur += tot
continue
else:
break
ans = 0
for j in range(min(m, 2)):
for i in range(n):
ans += cur == target
cur += s[i] == '1'
print(ans)