Plzz explzin how to do it…it doesn’t have any editorial.
here is question link:CodeChef: Practical coding for everyone
I tried solving it using tree linearization with segment tree(Also known as “Euler tour” as mentioned in the end). Now, what all of it means. Lets take the below tree as an example.
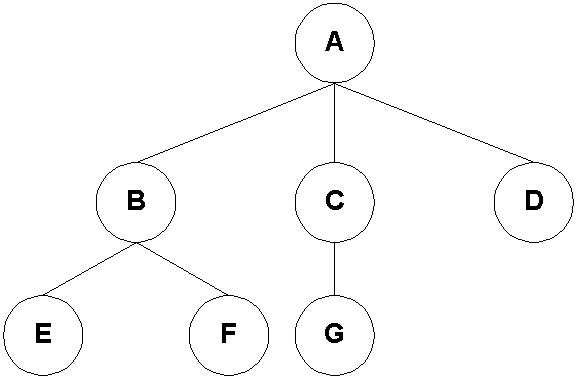
Here, if you do a DFS from A and keep adding the vertices as you visit them in a C++ vector, you will get something like this: V = [A, B, E, F, C, G, D] .
If you record the start time and the end time of each vertex. For example start time of A is 1, start time of B is 2, etc and end time of A is 8 and end time of B is 5. End time might be a bit confusing but endTime[Node] = Time when this node is finished being visited+1.
The crucial observation in this array is that for each node [startTime[Node], endTime[Node]) (This is just the subarray with index starting at starTime[Node] and ending at endTime[Node] but not containing it).
Now we have an array where a subarray corresponds to a subtree, what now? Now for the purpose of this problem, we can use a segment tree on this array to support both the operations. Suppose, we want to add X to all nodes in subtree of B, we can just add X to all elements in the subarray [startTime[B], endTime[B]), using segment tree it’s a trivial task. also it’s now trivial to support the queries of read type.
I hope I could explain you my idea. I don’t know why I got WA here, either it maybe some implementation bug or maybe my logic is wrong overall.
NOTE: This idea is not only applicable for this problem, this can actually be used for any problem with subtree queries. This has a well known name: “Euler tour”.