Can somebody please explain how to approach this problem?
PROBLEM LINK: CodeChef: Practical coding for everyone
@everule1
Yikes, there’s a lot to do here.
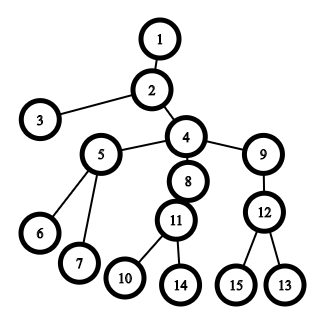
Let’s start with the example graph. We broke it down into the groups, like this
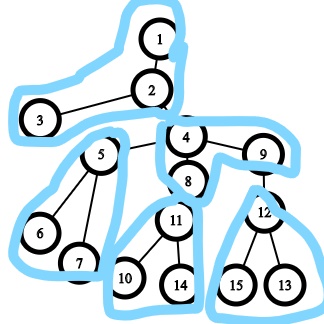
//Yes that’s the best I can edit.
Notice that some of them are subtrees. And iteratively removing them, will make all the groups a subtree eventually. But how do we prove this to be true.
Let’s try contradiction. Say If it wasn’t a subtree. If we removed it, It would leave us with two trees, one of them being a subtree of the initial tree. Therefore It would have become a subtree eventually anyways, so we don’t need to account for it.
So let’s start. Which subtree can I choose? Before asking this, we need to take note of a trivial observation.
The number of nodes must be a multiple of m, to be able to divide it equally into groups of n/m.
Now let’s start the bulk of the procedure. Say, we need a subtree of size n/m(let’s call that k), and that’s well and good, but what about the ones that are not subtrees initially?
Now we need to notice a very important point here.
When we remove a subtree, the size of the subtree either remains constant, or reduces by k. So for a node to be able to have a subtree of size k, it must have initially had a subtree of size ak with arbitrary a. So we need m such nodes right?
What if the node with a subtree ak doesn’t have a subtrees of size k. Then our method wouldn’t work.
Luckily, we can prove that it is not possible to generate such a configuration
Let’s try proving it
So we can start by ignoring the subtree, since the size of all the subtrees will still be a multiple of k as shown earlier. Now we have removed ak elements and we have a graph of n-ak elements has n/k -1 nodes with size as a multiple of k. Now we need at least n-k elements to produce such a graph.
Why?
For each subtree we’ll need at least k elements. Because, to join to subtrees of size xK and yK, and get another subtree of size zK, z must be at least x+y+1, since the joining node creates an extra node, and for the subtree size to divide k, we’ll need k nodes.
So It is sufficient to find m nodes with size a*k.
Now how can we do this in the time limit?
Let’s analyse the time complexity
DFS - O(n)
Each query -O(x)
This will not pass the Time limit.
Let’s analyse for how many x will there actually exist a answer
The number of factors of a number is approximately n^{1/3}
Now the sum of their factors is actually somewhere around nlog n,But this is not a strict upper bound, this does not hold for larger n. So if we memoise the answer and only compute it for those that have a answer, we should get
O(q+nlog\ n)
Tell me If I got something wrong, because I don’t trust myself.
//Also I just realised I don’t know how to make drop downs or large text, so If someone could tell me how to do that, that would be nice.
[details="wrapper"]
Wrapped text
[/details]
produces
wrapper
Wrapped text
Hope this helps. 
Thanks a lot brother ,will let you know in case I don’t get any part of your solution