Hi, I was trying to solve this problem
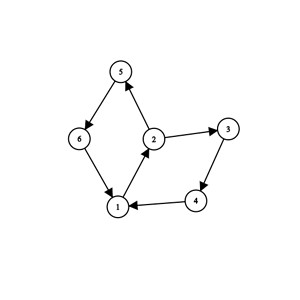
My approach to this was like just checking if the size of the SCC which contains the queried node is greater than equal to k or not if it is then the answer is Yes else it is No. But one can easily see that its not the intended solution if we consider the following test case :
all nodes here are in one strongly connected component say if we query for node 2 with k = 6 then we will get a Yes from above solution (as the size of this SCC is 6) but we can see that we will visit node 1 again in a path to 2 starting from 2 itself. Though answer would be correct for k’s which are less than 4
Can somebody please help with the correct solution for this problem?
@everule1 @rahul_g
AC code (just for reference)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll ;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef vector<ll> vi;
typedef vector<pll> vpll;
typedef unordered_map <ll,ll> umap ;
//#pragma GCC optimize "trapv"
#define loop(i,a,b) for(ll i=a ;i<b;i++)
#define For(i,n) for(int i=0;i<(ll)n;i++)
#define Rev(i,n) for(int i=n-1;i>=0;i--)
#define Rep(i,n) for(int i=1;i<=n;++i)
#define F first
#define S second
#define pb push_back
#define em emplace_back
#define all(v) (v).begin(),(v).end()
#define mems(x, y) memset(x, y, sizeof(x))
#define sz(v) (v).size()
#define mp(a,b) make_pair(a,b)
#define pf(n) cout<<n<<"\n"
#define pff(n) cout << n << " " ;
#define ar array
#define endl "\n"
#define int ll
#define time cerr << "\nTime elapsed: " << 1000 * clock() / CLOCKS_PER_SEC << "ms\n";
long const M=1e9+7;
const long mxN =1e5+2 ;
int n,m,k,q;
// Kosaraju's Algorithm for SCCs
vi adj[mxN],radj[mxN],order,component;
bool visited[mxN],ans[mxN] ;
void dfs1(int v){
visited[v]=1 ;
for(int x:adj[v])
if(!visited[x])
dfs1(x) ;
order.pb(v) ;
}
void dfs2(int v){
visited[v]=1 ;
component.pb(v) ;
for(int x:radj[v])
if(!visited[x])
dfs2(x) ;
}
void solve(){
cin >> n >> m >> k ;
mems(visited,0) ;mems(ans,0) ;
For(i,m){
int u,v ;
cin >> u >> v ;
adj[u].pb(v) ;radj[v].pb(u) ;
}
Rep(i,n)
if(!visited[i])
dfs1(i) ;
reverse(all(order)) ;
mems(visited,0) ;
for(int i:order)
if(!visited[i]){
dfs2(i) ;
if(sz(component)>=k)
for(int x:component)
ans[x]=1 ;
component.clear() ;
}
cin >> q ;
For(i,q){
int x; cin >> x ;
cout << (ans[x]?"Yes":"No") << endl ;
}
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
//cout << setprecision(20) << fixed ;
solve() ;
//ll t ; cin >> t ; while(t--)solve();
return 0;
}