Problem - SPOJ.com - Problem BENEFACT
I am new to Graphs.I have studied the basic Algorithms.
Please anybody help me in understanding how to go with the problem.
Can Anybody help?
Just pick an arbitrary node 1. Find the node that’s furthest away from 1, and then find the node that’s furthest away from that. This distance is the answer.
1 Like
@everule1 thanks for your reply,
But i did’nt understand why we are doing the second part
After finding the farthest point from node 1 why we are finding the next farthest point?Please explain @everule1.
Thank you so much in advance!
Oh right. Node 1 doesn’t need to be an endpoint of the longest path.
1 Like
First thing to note, while not particularly important, that the endpoints will be leaves of the tree, and that there is only one path between 2 nodes of a tree graph, without
crossing a vertex twice, so that is also the shortest path.
Basically the proof is that given 2 nodes, and a root, the path will go up and then come down. Let’s start with the case where the largest path turns at node 1 itself. The longest path would be 2 of the furthest leaves in 2 different branches. In which case our algorithm would very clearly be correct.
Now say that instead the point at which the largest path turns is at some other node. To prove that one of the endpoints consists of a node that’s furthest away from 1, Let’s call the distance from 1 to the node at which it turns d, and let’s call that node h
Now given that it turns at h, the leaf in the other branch of h, not containing the furthest node is larger than d + furthest node in some other branch of 1, otherwise we would take that path. But if that is the case, That means This node is deeper than all the other leaves from 1. Therefore The largest path always has a endpoint at the node furthest away from any given node.
I’ve made an assumption that d is positive. This method does not work for negative edge lengths.
1 Like
This requires a bit of drawing to see what exactly is going on.
1 Like
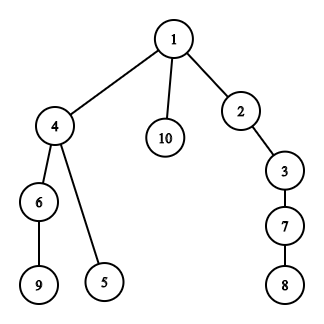
The maximum distance of a pair of nodes whose shortest path passes through 1, Is the sum of the 2 largest depths of its branches.
The depth of the branch with 4 is 3.
The depth of the branch with 2 is 4.
The depth of the branch with 10 is 1.
The sum of the 2 deepest branches is 7.
And so is the distance between 9 and 8, the longest path in the graph.
This is also applicable to weighted graphs.
1 Like
i understood the diagram
1 Like
but why you said this?
Till 1 it’s going up and then it’s going down to 8. Basically this logic also applies to subtrees of the graph.
1 Like
here d is 7?
if we consider that longest path is from node 1
Oh I accidentally used d for both the index and the distance, I’ll fix it.
1 Like
No problem.I was confused with d though! 
Can you explain it as simple as possible?What is it saying?
Just please explain it as simple as possible
@everule1