PROBLEM LINK: CodeChef: Practical coding for everyone
Author: Himanshu Khandelwal
Editorialist: Himanshu
DIFFICULTY:
MEDIUM
PREREQUISITES:
DP, Math
PROBLEM:
Find optimal partitioning of an array subject to constraints such that weight is maximized as mentioned in the problem.
EXPLANATION:
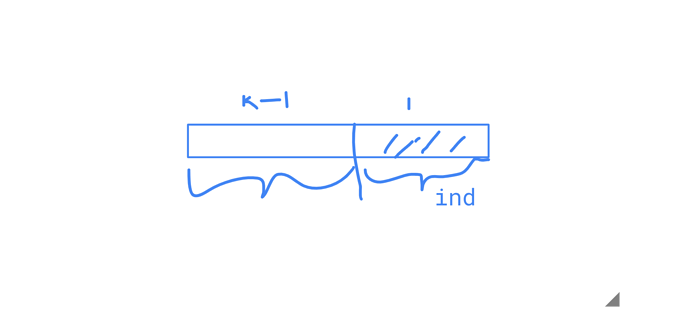
Memoize the recurrence relation to find the solution.
find(ind,k) = [for all i>ind&&i<n] max(find(i,k-1)+round(sum(ind, i-1)))
SOLUTIONS:
Setter's Solution
/*
Author: @himkha_100
Himanshu Khandelwal, NITW
*/
#include<bits/stdc++.h>
#define MOD 1000000007
#define INFI 1e15
#define INFIM 1e18
#define ll long long int
#define s(t) scanf("%lld",&t)
#define p(t) printf("%lld\n",t)
#define pb push_back
#define f(t) for(int i=0;i<t;i++)
#define fi first
#define se second
#define all(t) t.begin(),t.end()
#define ci(t) cin>>t
#define co(t) cout<<t
#define mii map<int,int>
#define pii pair<int,int>
using namespace std;
struct node{
int val;
int pos;
};
bool ac(int x,int y)
{
return x>y;
}
ll a[3001];
ll k;
ll n;
ll dp[3001][11];
ll pre[3005];
ll sum(int x, int y)
{
return pre[y+1]-pre[x];
}
ll round(ll k)
{
int l=k%10;
if(l>=5)
{
return k+10-l;
}
else
{
return k-l;
}
}
ll find(int ind, int k)
{
if(dp[ind][k]!=-1) return dp[ind][k];
if(k==1||ind==n-1)
{
return dp[ind][k]=round(sum(ind,n-1));
}
else
{
ll ma=0;
for(int i=ind+1;i<n;i++)
{
ll b=round(sum(ind,i-1))+find(i,k-1);
ma=max(ma,b);
}
return dp[ind][k]=ma;
}
}
int main()
{
int t;
cin>>t;
while(t--)
{
f(3001)
{
for(int j=0;j<11;j++)
{
dp[i][j]=-1;
}
}
s(n);
s(k);
k=min(k,n);
pre[0]=0;
f(n)
{
s(a[i]);
pre[i+1]=pre[i]+a[i];
}
p(find(0,k));
}
return 0;
}