PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author: raysh07
Tester: sushil2006
Editorialist: iceknight1093
DIFFICULTY:
Simple
PREREQUISITES:
None
PROBLEM:
Given A and B, does there exist some integer with A odd divisors and B even divisors?
EXPLANATION:
Every number has at least one odd divisor (that being 1), so if A = 0 we can immediately say that no solution exists.
What about even divisors?
It’s definitely possible for a number to not have any even divisors: specifically, note that odd numbers don’t have any even divisors.
So, suppose we have B = 0, i.e. we want no even divisors.
Our aim is to then find an odd number that has exactly A divisors.
This is always possible: for example, consider N = 3^{A-1}.
The divisors of 3^{A-1} are exactly 1, 3, 9, \ldots, 3^{A-1}, or 3^0, 3^1, 3^2, \ldots, 3^{A-1}.
There are of course A such divisors, and they’re all odd so we have what we want.
(Note that 3 isn’t special here - any p^{A-1} where p is an odd prime will work).
Next, we need to solve for B \gt 0, i.e. find a number which does have some even divisors.
Such an N must be even, obviously.
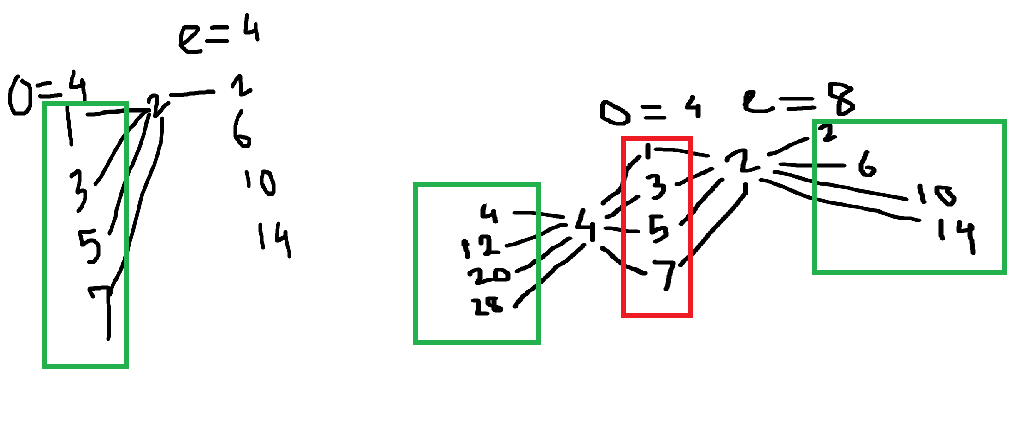
From the solution to the B = 0 case, we can see that powers of elements are important - so let’s look at the powers of 2 present in N.
That is, suppose we have N = 2^k \cdot M, where k \gt 0 and M is odd.
Now, observe that if d is any odd divisor of N, it will give rise to the even divisors 2d, 4d, 8d, \ldots, 2^k\cdot d.
That is, for each odd divisor of N, we obtain exactly k even divisors of N.
This means the number of even divisors of N must be exactly k times the number of odd divisors!
In other words, if B is not a multiple of A, then no solution can exist.
When B is a multiple of A, a valid N always exists: by combining the two ideas above, we can choose N = 2^k\cdot 3^{A-1}, where k = \frac{B}{A}.
This has A odd factors (that being 3^0, 3^1, \ldots, 3^{A-1}), and each odd factor gives us \frac{B}{A} even factors so there are B even factors in total, as we wanted!
So, quite simply, the answer is "Yes" if A\gt 0 and B is a multiple of A, and "No" otherwise.
TIME COMPLEXITY:
\mathcal{O}(1) per testcase.
CODE:
Editorialist's code (PyPy3)
for _ in range(int(input())):
a, b = map(int, input().split())
print('Yes' if a > 0 and b%a == 0 else 'No')