PROBLEM LINK:
Setter- Hasan Jaddouh
Tester- Ivan Safonov
Editorialist- Abhishek Pandey
DIFFICULTY:
SIMPLE
PRE-REQUISITES:
2-D Arrays, Bitwise Operations, Logical Reasoning.
PROBLEM:
Given a 2-D array of size N\times M, where elements are either 0 or 1. We can apply operation of OR’ING an entire row/column with another. We need to find minimum number of moves to make a particular cell A_{ij}=1. This must be done for all cells independently.
QUICK EXPLANATION:
Key Strategy- Deducing that its simple case-making, along with apt application of data structures is the key to get quick AC here.
We know that ans is -1 only if all elements are 0. If even 1 element is 1, it is possible to make the all other array elements 1 as well. Obviously, if A_{ij}=0 for some (i,j) and there is any cell in same row or column which is 1, then we can make A_{ij}=1 in a single move. Else, it will always take 2 moves.
EXPLANATION:
The editorial will have 4 sections. The first one will discuss when answer is 0, second when ans is 1, the next will discuss when answer is 2 and last one will discuss if answer is -1.
1. When answer is 0-
0 moves signify that no moves are needed to make A_{ij}=1. This is possible if and only if A_{ij}=1 initially in the input array. This is because, if A_{ij}=0, we will need at least 1 move to make it 1.
2. When answer is 1-
This is the case if A_{ij} lies in either same row, or same column with another cell A_{kl} such that A_{kl}=1. In this case, we can directly apply the given operation to make A_{ij}=1. An example illustration is given below-
Click to view
3. When answer is 2-
This section has 2 parts. The first part is to prove that “If any single element of array is 1, then its possible to make the entire array 1.”
Have an attempt and then look at the hidden box to see the proof details.
Click to view
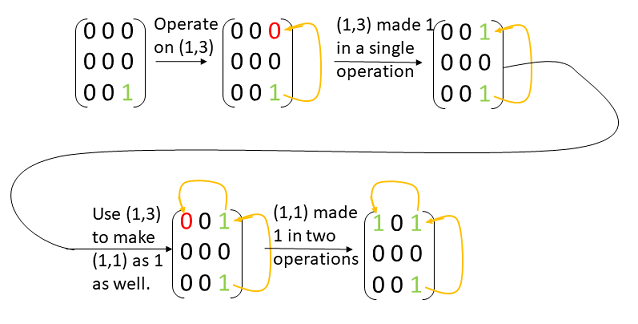
Say we have cell (i,j) as 1, i.e A_{ij}=1. Say we want to turn cell (x,y) to 1, i.e. A_{xy}=0 and we want to make it 1. Now, we can apply operation from row/column to any other row or column. Lets apply operation on row i and row x. We used operation once here.
Now, we got at least one 1 in row x. Say this cell is (x,z). We got A_{xz}=1. Now simply apply operation from column z to column y. We obtained A_{xy}=1 in only 2 operations.
Note that in this proof, cell (i,j) and (x,y) can be any general cells, we made no special assumptions. Hence, we can say that any cell can be made 1 in AT MOST 2 operations. We may use even lesser if special assumptions hold (eg- A_{xy}=1 already, or there is a single 1 in row x or row y), but it will never take more than 2 operations.
Look at the proof above in case you didnt. Notice that, we made the target cell 1 in 2 operations, and we used no special assumptions - i.e. we talked for any general cells. Hence, 2 is a upper bound on number of operations. If no special assumptions like above hold, then answer is always 2.
An illustration of above is given in tab below for reference-
Click to view
4. When answer is -1 -
Refer to proof in above section. We proved that if at least one cell A_{ij}=1, then we can make entire array as 1. Hence, the answer is -1. if and only if, there is no element A_{ij}=1, i.e. all elements are 0. Then, we cannot make any cell -1.
SOLUTION:
As a convenience to fellow readers, I have also copy pasted the codes in tabs below. Please refer to them while @admin links the solutions to the editorial Thank you ![]()
Click to view
#include <iostream>
#include <algorithm>
#include <string>
#include <assert.h>
using namespace std;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
int T;
int n,m;
int row[1010];
int column[1010];
string fld[1010];
int sm_nm = 0;
int main(){
T=readIntLn(1,100);
while(T--){
n=readIntSp(1,1000);
m=readIntLn(1,1000);
sm_nm += n*m;
assert(sm_nm<=1000000);
bool found=false;
for(int i=0;i<n;i++){
fld[i] = readStringLn(m,m);
for(int j=0;j<m;j++){
assert(fld[i][j] == '0' || fld[i][j] =='1');
if(fld[i][j]=='1'){
row[i] = 1;
column[j] = 1;
found = 1;
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(!found){
cout<<-1<<" ";
} else {
if(fld[i][j] == '1'){
cout<<0<<" ";
} else if(row[i] || column[j]){
cout<<1<<" ";
} else {
cout<<2 << " ";
}
}
}
cout<<endl;
}
}
assert(getchar()==-1);
}
Click to view
#include <bits/stdc++.h>
#include <cassert>
using namespace std;
typedef long long ll;
typedef long double ld;
// read template
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
// end
const int M = 1e3 + 239;
ll sum;
bool a[M], b[M];
int n, m;
string s[M];
void solve()
{
//n = readIntSp(1, 1000);
//m = readIntLn(1, 1000);
cin >> n >> m;
sum += (ll)n * (ll)m;
for (int i = 0; i < n; i++) cin >> s[i]; //s[i] = readStringLn(m, m);
bool ch = true;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
ch &= (s[i][j] == '0' || s[i][j] == '1');
assert(ch);
for (int i = 0; i < n; i++)
{
a[i] = 0;
for (int j = 0; j < m; j++) a[i] |= (s[i][j] - '0'); //is any 1 in i-th row
}
for (int j = 0; j < m; j++)
{
b[j] = 0;
for (int i = 0; i < n; i++) b[j] |= (s[i][j] - '0'); //is any 1 in j-th column
}
ch = false;
for (int i = 0; i < n; i++) ch |= a[i];
for (int i = 0; i < n; i++, cout << "\n")
for (int j = 0; j < m; j++, cout << " ")
{
if (!ch) cout << -1; // ch = 0 ==> all s[i][j] = 0 ==> all answers = -1
else if (s[i][j] == '1') cout << 0; // answer is 0, because s[i][j] = 1
else if (a[i] || b[j]) cout << 1; // it can be done in 1 operation
else cout << 2; // it can be done in 2 operations
}
}
int main()
{
//int T = readIntLn(1, 100);
int T;
cin >> T;
sum = 0;
while (T--) solve();
//assert(getchar() == -1);
assert(sum <= (ll)(1e6));
return 0;
}
Time Complexity= O(N*M) (for input).
Checking if there is a 1 in given row or column is checked in O(1) by doing a O(N*M) pre-processing before hand while taking input.
CHEF VIJJU’S CORNER 
1. There is an interesting version of problem. Given a 2-D array, with some 1 and 0's as values of array elements, solve the following-
- Find the row with maximum 1's given that all 1's lie before all 0's.
- Find row with minimum 1's if all 0's like before all 1's.
- Given any general array, find minimum number of moves to make any row OR column all 1.
For each of the three questions, either prove that they arent solvable in polynomial time, or give an algorithm which solves them in polynomial time.
2. One major part of this question is checking if there is a 1 in same row or column. How will you do that? Lets have a look at this idea -
“For every cell (i,j) such that A_{ij}=1, store i in a vector rows and store j in another vector column. Now, for each cell (x,y) such that A_{xy}=0, just binary search if x exists in rows or y exists in columns.”
Is this correct? Is this the best time complexity we can use? Answer these w.r.t. the above idea.
(Hint: Refer to setter’s solution)
3. Getting a WA? Does your code use int arr[n][m]={}; anywhere? Its UNDEFINED BEHAVIOUR and causes your code to print garbage values to judge when submitting. Specify the dimensions of an array as a number only!!
