PROBLEM LINK:
Contest Div 1
Contest Div 2
Contest Div 3
Practice
Setter: flamestorm153
Tester: Anshu Garg
Editorialist: Keyur Jain
DIFFICULTY
Easy
PREREQUISITES
Manhattan DIstance
PROBLEM
Chef has an array A with N elements. He wants to find N points P_1, \dots, P_N with integer coordinates on the 2D coordinate plane such that, for all pairs of indices i and j (1 \leq i \lt j \leq N), the Manhattan distance from P_i to P_j is A_i+A_j. Help him find any N points satisfying the condition, or state that no such points exist.
As a reminder, the Manhattan distance between the points (x_1, y_1) and (x_2, y_2) is defined as |x_1 - x_2| + |y_1 - y_2|.
QUICK EXPLANATION
- Answer is not possible for N > 4
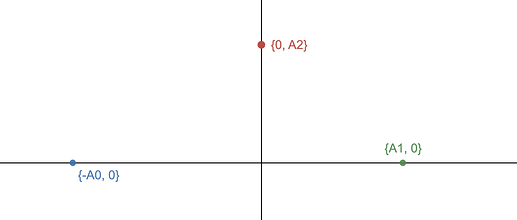
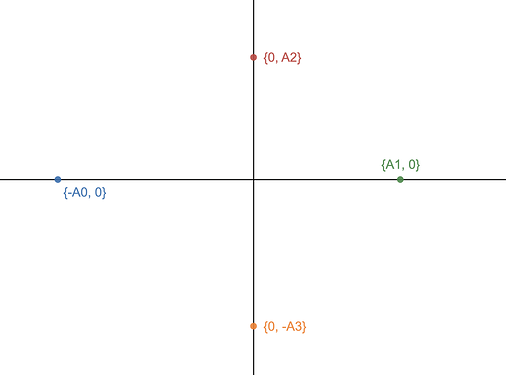
- For N <= 4, we choose one point on each of the axes (+X, -X, +Y, -Y). The final ans can be ((A_0, 0), (-A_1, 0), (0, A_2), (0, -A_3))
EXPLANATION
Lets try to solve for increasing N.
For N = 1, we can choose any point and we have a solution.
For N = 2, we can choose two points on a single line at a distance A_0 + A_1 apart. They can be (-A_0, 0) and (A_1, 0), two points on the X-axis. Note that there can be many solutions here.
For N = 3, this gets a little bit tricky. Let us assume that the first two points are (-A_0, 0) and (A_1, 0) and the third point is (x,y), so we solve for (x, y).
Three points that satisfy the constraints given in the question cannot be colinear. The proof is left as an exercise to the users. Hence, y != 0, since the two points we have chosen so far lie on the x-axis and will result in all three points being colinear. Let us also assume that y > 0, since the solution with y < 0 can be mirrored into the positive y direction.
We know that manhattan distance between P_0 and P_2 should be A_0 + A_2. This brings us to equation 1:
- (x + A_0) + y = A_0 + A_2
Similarly, using points P_1 and P_2 we get equation 2 :
- (A_1 - x) + y = A_1 + A_2
You can solve the above two equations along with y > 0 to get the solution as P_2 = (0, A_2)
for N = 4, we can try to find the fourth point in a similar way by creating three equations, one each for the manhattan distance between (x,y) and the existing points, and we would end up with the solution P_3 = (0, -A_3).
for N >= 5, no solution exists.
One way would be to try to solve for a point (x, y) that is equidistance from a set of valid points.
Alternatively, for each point we draw a manhattan circle centred at it with radius A_i. The condition implies that each pair of circles forms a tangent.
Since (under manhattan metric) each circle is actually a square, it only has four corners and four sides. Hence it follows that at most four circles can be pairwise tangents, and at most four points can be pairwise equidistant from each other.
TIME COMPLEXITY
The time complexity of the solution itself is O(1)
The time complexity including the time for parsing input is simply O(N)
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
const int MAX = 200007;
const int MOD = 1000000007;
const int d[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
void solve() {
int n;
cin >> n;
int a[n + 7];
for (int i = 0; i < n; i++) {
cin >> a[i];
}
if (n > 4) {cout << "NO\n";}
else {
cout << "YES\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < 2; j++) {
cout << d[i][j] * a[i] << ' ';
}
cout << '\n';
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int tt; cin >> tt; for (int i = 1; i <= tt; i++) {solve();}
// solve();
}
Tester's Solution
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
const int M = 1000000007;
const int MM = 998244353;
template<typename T, typename U> static inline void amin(T &x, U y){ if(y<x) x=y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x<y) x=y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2351
#endif
long long readInt(long long l,long long r,char end){
long long x = 0;
int cnt = 0;
int first =-1;
bool is_neg = false;
while(true) {
char g = getchar();
if(g == '-') {
assert(first == -1);
is_neg = true;
continue;
}
if('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if(cnt == 0) {
first = g - '0';
}
++cnt;
assert(first != 0 || cnt == 1);
assert(first != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && first > 1)));
}
else if(g == end) {
if(is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
assert(false);
}
}
}
string readString(int l,int r,char end){
string ret = "";
int cnt = 0;
while(true) {
char g = getchar();
assert(g != -1);
if(g == end) {
break;
}
++cnt;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
// check N = 1, 2, 3, 4
// check when coordinates exceed 1e18 or shifting them
// check when returning N > 4 we return before taking the input
// try outputting extra integers to verify checker
int sumN = 0;
int _runtimeTerror_()
{
int N = readIntLn(1,2e5);
// int N; cin >> N;
vector<int> a(N);
for(int i=0;i<N;++i) {
// cin >> a[i];
// continue;
if(i == N - 1) {
a[i] = readIntLn(1,1e9);
}
else {
a[i] = readIntSp(1,1e9);
}
}
sumN += N;
assert(sumN <= 2e5);
if(N > 4) {
cout << "No\n";
return 0;
}
vector<int> dx = {-1,1,0,0}, dy = {0,0,1,-1};
cout << "yES\n";
for(int i=0;i<N;++i) {
cout << a[i] * dx[i] + (ll)(-1e17) << " " << a[i] * dy[i] + (ll)(-1e17) << "\n";
}
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initialize();
#endif
int TESTS = 1;
// cin >> TESTS;
TESTS = readIntLn(1,1e4);
while(TESTS--)
_runtimeTerror_();
assert(getchar() == -1);
return 0;
}
Editorialist's Solution
public class ChefAndPairwiseDistances {
public void solve(int testNumber, InputReader in, OutputWriter out) {
int n = in.readInt();
int[] arr = in.readIntArray(n);
if (n > 4) {
out.printLine("NO");
} else {
out.printLine("YES");
out.printLine(-arr[0], 0);
if (n > 1) {
out.printLine(arr[1], 0);
}
if (n > 2) {
out.printLine(0, -arr[2]);
}
if (n > 3) {
out.printLine(0, arr[3]);
}
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()