Problem LInk : CodeChef: Practical coding for everyone
A number is divisible by 9, if the sum of the digit is divisible by 9.
Image for reference:
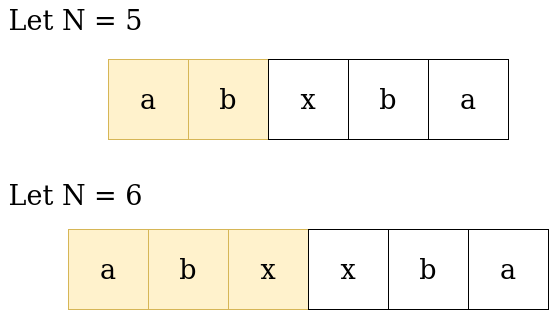
For N belongs to odd except 1,
There always exist a unique x for which the sum is divisible by 9 i.e.
( 2*(a + b) + x ) % 9 = 0
For every a, b , there exist a unique x
Example :
for N = 5 ,a = 4 ,b = 9
a + b + x + b + a => 26 + x must be div by 9
Then x must be 1.
So the number of pallindromes, if the length is odd is pow(9, len/2 ).
Similarly for N = even
Let N = 6
For every a, b , there always exist a unique x to make sum div by 9 i.e.
( 2*(a + b + x)) % 9 = 0 // as in the case of odd
Example
For N = 6
a = 4
b = 9
a + b + x + x + b + a = 26 + 2x must be div by 9
Then x must be 5
So the number of pallindrome, if length is even ,is pow( 9, (len/2) – 1)
Now, the question left to calculate the sum of Numbers :
NOTE : THIS METHOD IS NOT VALID FOR N = 1 OR N = 2
Consider the Kth position in N.
At Kth position , each digit [0,9] will repeat {Total ways of forming favoulable pallindromes} / 9 times.
So, the sum of all the digits on Kth position = 45*{ways/9}
So the sum can be easily found, For ref see code.
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
#define MOD 1000000007
ll power(ll a, ll b)
{
if (b == 0)
{
return 1;
}
ll temp = power(a, b / 2);
temp = (temp * temp) % MOD;
if (b % 2 != 0)
{
temp = (temp * a) % MOD;
}
return temp;
}
int main()
{
ll test;
cin >> test;
while(test--){
ll len;
cin >> len;
// this method will not work for n = 1 and 2, so
if(len == 1){
cout << "9" << endl;
continue;
}
if(len == 2){
cout << "99" << endl;
continue;
}
ll ways = len / 2;
if (len % 2 == 0)
ways--;
ll res = power(9, ways-1);
ll sum = 0;
for (int i = 0; i < len; i++)
{
sum = sum * 10 + (45 * res );
sum = sum % MOD;
}
cout << sum << endl;
}
return 0;
}