PROBLEM LINK:
Practice
Div-1 Contest
Div-B Contest
Author: Yuriy Fedorov
Tester: Felipe Mota
Editorialist: Alei Reyes
DIFFICULTY:
EASY
PREREQUISITES:
Vectors, Convex-Hull
PROBLEM:
There are N vertical segments, the i-th with endpoints (i,0), (i,h_i).
The segment j is vissible from segment i, if the segment (i, h_i), (j,h_j) does not intersect another vertical segment.
Find the pair (i,j) such that j is vissible from i, and |j-i| is maximum.
QUICK EXPLANATION:
Build the convex hull of the points (i,h_i) from right to left (in decreasing order of i), the rightmost vissible point from i is given by the segment of the convex hull that starts at (i,h_i).
EXPLANATION:
Let’s denote the top of the i-th segment by P_i = (i,h_i), and let nxt[i] be the maximum j such that j is vissible from i.
Subtask 1
Let’s brute force each pair (i,j) and iterate over each i \lt k \lt j to determine if the vertical segment (k,0), (k,h_k) intersects (i,h_i), (j,h_j).
We can use vectors to check the intersection, the cross product allows us to determine if two segments are in clockwise or anti-clockwise by looking to the sign of (P_j - P_i) \times (P_k-P_i). It is also possible to use geometry and calculate the equation of the lines, and their intersection, however vectors make it easier. The complexity of this approach is O(N^3).
Subtask 2 and 3
The plan to is optimize our solution by finding nxt[i] using the values of nxt[i+1],nxt[i+2], \ldots, nxt[N].
Let j=nxt[i] and k=nxt[j], note that we should always go in clockwise direction i.e (P_k-P_j) \times (P_j-P_i) \gt 0, otherwise it would be possible to see k from i (a contradiction).
Let’s draw a segment from each P_i to P_{nxt[i]} and look at the sequence of points H_i = (P_i, P_{nxt[i]}, P_{nxt[nxt[i]]}, ...). The idea is to reuse the information gathered in H_{i+1} to find nxt[i].
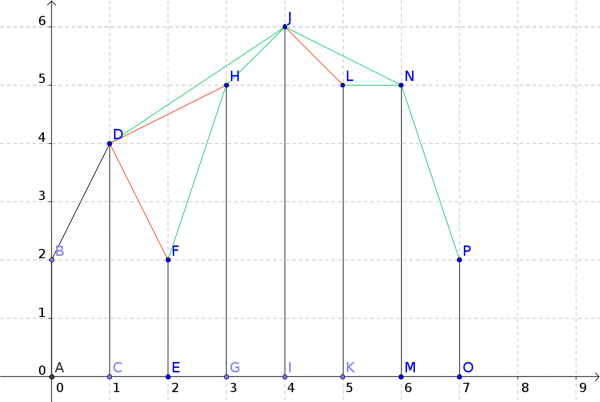
For example in the above picture H_F = (F, H, J, N, P), the green lines represent the segments with endpoints P_i, P_{nxt[i]}.
To calculate nxt[i] we have to find the smallet j such that the points P_i, H_{i+1,j} and H_{i+1,j+1} are clockwise. For example, in the picture to find nxt[D] we have to look at the sequence H_F and discard F because DFH are not clockwise, similarly H is discarded and nxt[D]=J. The red lines represent the discarded segments.
If the previous algorithm is implemented naively you will get a quadratic complexity (subtask 2), however note that to determine nxt[i] we have to remove a preffix of H_{i+1}, that means each point is removed and added once, so the complexity is linear. Note that the sequence H_i is actually the upper-hull of the points P_i, \ldots ,P_N.