PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Contest Division 4
Setter: TheScrasse
Tester: Abhinav Sharma, Lavish Gupta
Editorialist: Devendra Singh
DIFFICULTY:
1098
PREREQUISITES:
None
PROBLEM:
You are given an integer N. Let A be an N \times N grid such that A_{i, j} = i + N\cdot(j-1) for 1 \leq i, j \leq N. For example, if N = 4 the grid looks like:

You start at the top left corner of the grid, i.e, cell (1, 1). You would like to reach the bottom-right corner, cell (N, N). To do so, whenever you are at cell (i, j), you can move to either cell (i+1, j) or cell (i, j+1) provided that the corresponding cell lies within the grid (more informally, you can make one step down or one step right).
The score of a path you take to reach (N, N) is the sum of all the numbers on that path.
You are given an integer K that is either 0 or 1. Is there a path reaching (N, N) such that the parity of its score is K?
Recall that the parity of an integer is the (non-negative) remainder obtained when dividing it by 2. For example, the parity of 246 is 0 and the parity of 11 is 1. In other words, an even number has parity 0 and an odd number has parity 1.
EXPLANATION:
When N is even, an answer always exists irrespective of the value of K.
N is even
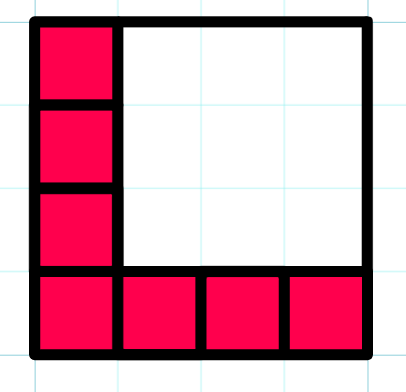
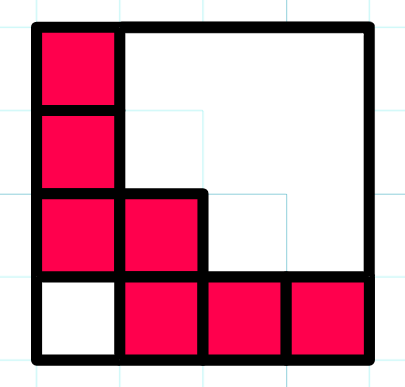
Choose a path similar to one of the two paths shown above. We can show that these paths have different parities and exactly one of these paths has parity equal to K. There is a difference of one cell in both of these paths and these cells have different parity.
A_{N,1} = N\cdot (N-1)+1 which is odd as N is even
A_{N-1,2} = N\cdot (N-2)+2 which is even as N is even
Hence both of these paths have different parities and we can choose one which has the parity of sum equal to K
In case when N is odd, answer exists only when K=1
N is odd
All paths of odd length (number of cells here) end at an odd value and all the paths with even length end at at even value. For length 1 it is true as A_{1,1} =1 odd.
Let us suppose this is true for general length L. Let the path end at an index A_{i,j} and the length of path is odd. This means by our assumption A_{i,j} is odd.
\therefore A_{i,j} = N\cdot (i-1) +j is odd
\implies A_{i,j+1} = N\cdot (i-1)+j+1 is even
\implies A_{i+1,j} = N\cdot (i)+j= A_{i,j}+N is even (as N is odd)
Similarly we can show the same for even length paths.
Therefore the claim is true by induction. Since, N is odd therefore the path length is odd and the paths looks like odd -> even -> odd -> … . …odd, where odd number occurs N times and even number occurs N-1 times. Odd(N) times addition of odd numbers is an odd number and addition of an odd number and even number is also odd. Therefore the parity of path in case of odd N is always odd.
TIME COMPLEXITY:
O(1) for each test case.
SOLUTION:
Setter's Solution(Python)
for _ in range(int(input())):
n, k = map(int, input().split())
print('yes' if n%2 == 0 or n%2 == k else 'no')
Editorialist's solution
#include "bits/stdc++.h"
using namespace std;
#define ll long long
#define pb push_back
#define all(_obj) _obj.begin(), _obj.end()
#define F first
#define S second
#define pll pair<ll, ll>
#define vll vector<ll>
ll INF = 1e18;
const int N = 1e5 + 11, mod = 1e9 + 7;
ll max(ll a, ll b) { return ((a > b) ? a : b); }
ll min(ll a, ll b) { return ((a > b) ? b : a); }
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
void sol(void)
{
int n, k;
cin >> n >> k;
if (n % 2 == 0)
cout << "YES\n";
else if (k)
cout << "YES\n";
else
cout << "NO\n";
return;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int test = 1;
cin >> test;
while (test--)
sol();
}