PROBLEM NAME: Alice and Mex
DIFFICULTY : Medium
PREREQUISITES : 2-pointer
PROBLEM : Alice has known the concept of MEX (Maximum excluded), which represents the minimum non-negative integer that does not belong to the array. For instance:
The MEX of [2,3,1,4] is 0 because 0 does not belong to the array.
The MEX of [1,1,0,2,2] is 3 because 3 does not belong to the array.
Bob challenges Alice and gives him an array A of length N and the task is to count the number of subarrays of A having MEX at least M.
Task: Determine the count of subarrays of array A which has the MEX at least M.
CONSTRAINTS :
1 <= T <= 100
1 <= N <= 10^5
0 <= X <= N
0 <= A[i] <= N
SAMPLE INPUT (1) :
3 2
1 0 2
SAMPLE OUTPUT (1) :
2
SHORT EXPLANATION :
The main observation of the problem is that for a subarray to have a MEX as M, it must have all integers [0, M-1] in it, Hence, we initialize two pointers left and right and for each left pointer, we keep moving the right pointer to the right until we cover all integers in the range [0, M-1] in the current window and keep incrementing the answer accordingly.
DETAILED EXPLANATION :
The main observation of the problem is that, suppose the required MEX is M, then for the subarray to have minimum MEX as M it must contain all integers in the range [0, M-1], let’s call this subarray good.
It can be observed that if A(left, right) is good then A(left,right+1) is good as well and if subarray A(left, right) is not good then A(left,right-1) is not good.
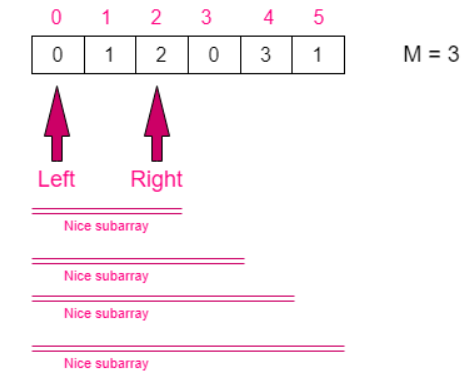
Hence, for each left end left, there is a unique right end right such that all subarrays A(left, right’) such that right <= right’ < N are good. We just need to find this right end right. There would be exactly N-right subarrays with that left end which are nice. If no such right exists, then assume r=N.
Thus, we count the number of subarrays in each of the Q queries
SOLUTION:
#include <bits/stdc++.h>
using namespace std;
#define watch(x) cout<<(#x)<<"="<<(x)<<'\n'
#define mset(d,val) memset(d,val,sizeof(d))
#define setp(x) cout<<fixed<<setprecision(x)
#define loop(i,a,b) for(int i=(a);i<(b);i++)
#define hunt(i,a,b) for(int i=(a);i<=(b);i++)
#define lp(i,a,b) for(int i = a; i >= b; i--)
#define rep(i,n) for(int i = 0; i < n; i++)
#define int long long int
#define pb push_back
#define f first
#define s second
#define pqueue priority_queue
#define fbo find_by_order
#define ook order_of_key
#define ll long long
#define ii pair<int,int>
#define vi vector<int>
#define vii vector<ii>
#define ld long double
#define all(x) begin(x),end(x)
void YES(){cout<<"YES\n";} void NO(){cout<<"NO\n";}
ll Bexp(ll a,int b){ ll ret=1; for (;b;a=a*a,b>>=1) if (b&1) ret=ret*a; return ret; }
ll gcd(ll A , ll B)
{
if(B == 0)return A;
return gcd(B , A%B);
}
ll min(ll a , ll b){return a > b ? b : a;}
ll max(ll a , ll b){return a > b ? a : b;}
int mod(int a, int b) {
return (((a % b) + b) % b);
}
const int MOD = 1e9 + 7;
void fastIO()
{
#ifndef vjudge
if (fopen("input.txt", "r"))
{
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
}
#endif
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
}
void solve(){
int n,x;
cin >> n >> x;
int cnt[n+1],A[n];
memset(cnt,0,sizeof cnt);
rep(i,n)cin >> A[i];
int mex=0,r=0;
//maintain the current mex to keep track wheather the subarray(l,r)
// has all values [0,x-1]
while(r < n && mex < x){
cnt[A[r]]++;
r++;
while(cnt[mex])mex++;
}
if(mex < x){
cout << 0 << endl;
return;
}
int ans = (n-r+1);
for(int l=1;l<n;l++){
--cnt[A[l-1]];
if(cnt[A[l-1]] == 0 && A[l-1] < x){
while(r < n && cnt[A[l-1]] == 0){
cnt[A[r]]++;
r++;
}
}
if((A[l-1]<x) && (cnt[A[l-1]] == 0))break;
ans += (n-r+1);
}
cout << ans << endl;
}
int32_t main() {
fastIO();
int t=1;
cin >> t;
for(int test=1;test<=t;test++){
solve();
}
}
TIME COMPLEXITY :
O(N) where N represents the number of elements
We are traversing the whole array once.
SPACE COMPLEXITY :
O(N), where N represents the number of elements