PROBLEM LINK:
Author: Abhishek Ghosh
Tester: Abhishek Ghosh
Editorialist: Kunal Nehra, Shivang Dua
DIFFICULTY
Easy-Medium
PREREQUISITES
Greedy, Two-Pointers
PROBLEM
We are given a peak array consisting of N integers and an integer K. Peak array is an array which consists of the integers first in strictly increasing order and then in strictly decreasing order. We need to find the array with maximum product at the end of K steps (product of an array means the product of all its elements).
In each step we can increase any one element of the array by 1 such that it still remains a peak array and has the maximum product possible at that step. We need to print the peak array at K^{th} step with the largest product.
(If multiple answers exist, then we print the lexicographically smallest one).
QUICK EXPLANATION
- We can have 2 pointers. One pointer (l) that will start from 0^{th} index and move rightwards but will never cross the peak element and another pointer (r) that will start from N-1 index and move leftwards but will never cross the peak element.
- Increasing the smaller number will make the product larger as compared to increasing the larger number. This is the greedy step that we take for each operation.
- At each level, ‘l’ will point to the minimum integer in its range such that on increasing a[l] by 1 the array remains a peak array, and similarly ‘r’ will point to the minimum integer in its range such that on increasing a[r] by 1 the array remains a peak array.
- At each step increase min(a[l],a[r]) by 1.
- If a[l]=a[r], then count the number of elements before a[l] i.e l and after a[r] i.e n-r-1.
If (l>n-r-1) then increase a[l] by 1. Otherwise, increase a[r] by 1. - After every step, there are always a maximum of 2 possible unique arrays.
EXPLANATION
First of all, we need to define two pointers l and r.
Pointer ‘l’ will start from 0^{th} index and can move in forward direction up to the index of the peak element. Pointer ‘r’ will start from the (N-1)^{th} index and can move in the backward direction up to the index of the peak element.
Observation:
Increasing the smallest number will make the product larger as compared to increasing larger numbers. So we will try to increase the smallest possible number at each step.
Now we will move the pointer ‘l’ to an element such that the element is minimum in the range of l as well as, on increasing the element the array should remain a peak array, and we do the same for the pointer ‘r’.
Both the pointers now point to that element on their respective sides which is the smallest element that can be incremented without violating the property of peak arrays.
Now there will be 3 cases :
Case 1 and 2 (unequal condition)
-
CASE 1:
a[l] < a[r]
Increase a[l] by 1. -
CASE 2:
a[l] > a[r]
Increase a[r] by 1.
Case 3 (equal condition)
- CASE 3:
a[l]==a[r]
Now we need to count the number of elements before a[l] and number of elements after a[r]. Number of elements before a[l] = l.
Number of elements after a[r] = n-r-1.
Now there will be 3 more cases under CASE 3:
- CASE 3(i): (l) > (n-r-1)
Increase a[l] by 1.
Decrease l by 1.- CASE 3(ii): (l) < (n-r-1)
Increase a[r] by 1.
Increase r by 1.- CASE 3(iii): (l) == (n-r-1)
In this case we will have the lexicographically smallest one as our peak array.
Increase a[r] by 1.
Increase r by 1.
The paths that we take at each step can be visualised in the form of a tree, where we have 2 choices. Either we can increase ‘l’ and move leftwards, or we can increase ‘r’ and move rightwards.
None of the remaining steps will ever result in maximum product at all the levels.
It is clear that there can be a maximum of 2 unique paths that are favourable.
Here are few examples for better understanding:
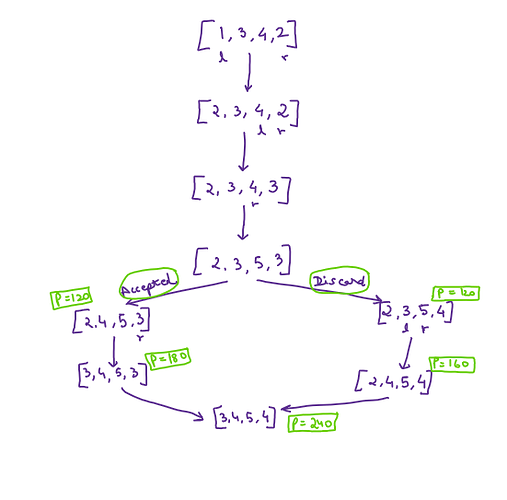
Example 1
Case 3(i)
Both the paths will merge at some step.
This is true for all possible arrays. But in this case, if we move rightwards, then [2,4,5,4] is the
most optimal on the right side with a product of 160, but this has to be discarded, since
[3,4,5,3] is the most optimal on the left side with a product of 180, thus we move leftwards.
Example 2
Case 3(iii)
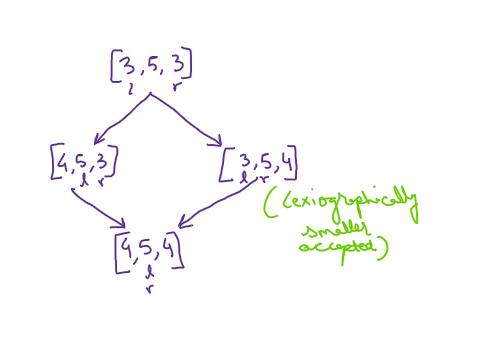
In this case we can move either of the 2 sides, as we are guaranteed to have at least one array with maximum products on each side. But since [3,5,4] is lexicographically smaller than [4,5,3], thus we move rightwards.
Optimization:
Every time the pointers move out of bounds, we do not have to start scanning from their starting indices. We can maintain ‘lmax’ which will be the maximum index ‘l’ has reached, and ‘rmin’ which will be the minimum index ‘r’ has reached.
If ‘l’ moves out of bounds, (l < 0) we can safely point ‘l’ at ‘lmax’.
If ‘r’ moves out of bounds, (r >= n) we can safely point ‘r’ at ‘rmin’.
TIME COMPLEXITY
O(N+K) for each test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int32_t main() {
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int T = 1;
cin >> T;
while(T--) {
int n, k;
cin >> n >> k;
vector<int> arr(n);
for(int &x : arr)
cin >> x;
int l = 0, lmax = 0;
int r = n-1, rmin = n-1;
while(k--) {
while(l < r && arr[l+1] > arr[l] && arr[l+1] == arr[l] + 1) {
l++;
}
lmax = max(lmax, l);
while(l < r && arr[r-1] > arr[r] && arr[r-1] == arr[r] + 1) {
r--;
}
rmin = min(rmin, r);
if(l == r) {
arr[l]++;
l--;
r++;
} else if(arr[l] < arr[r]) {
arr[l]++;
l--;
} else if(arr[l] > arr[r]) {
arr[r]++;
r++;
} else {
int right = n - r;
int left = l + 1;
if(left > right) {
arr[l]++;
l--;
} else {
arr[r]++;
r++;
}
}
if(l < 0) l = lmax;
if(r >= n) r = rmin;
}
for(int x : arr) {
cout << x << " ";
}
cout << "\n";
}
return 0;
}