PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Author: Soumyadeep Pal
Tester: Istvan Nagy
Editorialist: Aman Dwivedi
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Maths, Observation
PROBLEM:
You are given N distinct points in a 2-D plane, numbered 1 through N. The X-coordinate of the points are X_1,X_2,…,X_N respectively and the Y-coordinates are Y_1,Y_2,…,Y_N respectively. Your goal is to make the location of all the N points equal to that of each other. To achieve this, you can do some operations.
In one operation, you choose an index i(1\leq i\leq N) and a real number K and change the location of the i_{th} point in one of the following ways:
-
Set (X_i,Y_i)=(X_i+K,Y_i)
-
Set (X_i,Y_i)=(X_i,Y_i+K)
-
Set (X_i,Y_i)=(X_i+K,Y_i+K)
-
Set (X_i,Y_i)=(X_i+K,Y_i−K)
Find the minimum number of operations to achieve the goal.
QUICK EXPLANATION:
The only points that can yield minimum operations when every other given point has coincided with them are the ones to which a pair of points can be made equal to in 1 operation each.
We find all such points that can potentially be the meeting points leading to minimum operations. For each such point A, we calculate total operations needed to make the location of all N points equal to A and pick the minimum amongst these operations as answer.
EXPLANATION:
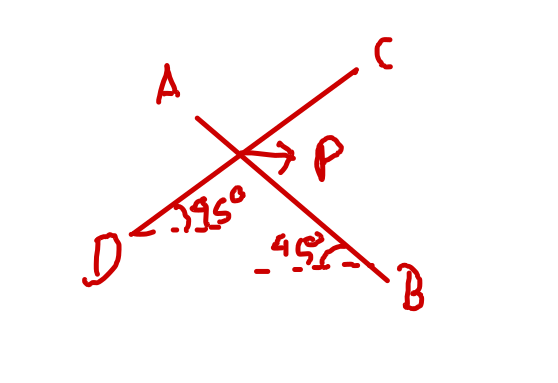
We can observe that a point is allowed to move in 8 directions with respect to the co-ordinate axis, namely {0\degree, 45\degree, 90\degree, 135\degree, 180\degree, 225\degree, 270\degree, 315\degree}
Consider any pair of given points, we can deduce from the given operations that making the location of these 2 points same can always be done in 1 operation per point as follows:
- If the points both lie on a line inclined to the axes at 45\degree in any of the 4 quadrants, then a single operation moving one of the points along this line to meet the other would suffice.
- If the points don’t lie on such a line, then bringing them to the same location would need:
- 1 operation if they lie on a horizontal or vertical line, i.e. moving one point along the horizontal or vertical line to the other as is allowed by the given operations.
- 2 operations otherwise, i.e. moving both points along the allowed directions, towards each other until they collide at the same point.
The maximum value of minimum number of operations to bring all points to same location would be 2*N.
Proof
Let A be considered as the meeting point and N the total number of points:
If N_1 number of points need a single operation to coincide with A and N_2 points need 2 operations, the minimum operations will be N_1+2*N_2 where N_1+N_2=N or N_1+N_2+1=N, in case one point is already positioned at A.
A single point can reach any other point in at most 2 operations, thus even if all points need 2 operations to reach an arbitrary selected meeting point, it will be achieved in a total of 2*N operations, 2 for each point.
We need to look for points where we can achieve a value less than 2*N. Selecting points which can be reached by a pair of points in at most 1 operation each will give us total operations less than 2*N (As stated at the beginning such a point always exists for every pair of points).
Proof
Consider a pair of points initially having to need 2 operations each to reach the meeting point. If we now change the meeting point to a location to which this pair of points can reach in a 1 operation each, we will be left with 2*N-2*2+2*1 total operations which is better than the initial 2*N.
Explaining how this approach is the optimal one
Since considering one of the 2 points in the pair itself as the potential meeting point also reduces the final answer, I will explain how these cases are also covered by the mentioned approach and needn’t be dealt with seperately.
Consider 2 points Y and Z. If we take one of the 2 points, say Y itself as the final location, our maximum value of minimum operations needed to make all points meet would change to 2*N-2. There are 2 possibilities arising as follows:
- No other number of operations are reduced except the ones for Y which changed from 2 to 0 (Since no 2 points are in the same location, no operations except that for Y itself can be 0).
- Operations needed for Y are 0 and number of operations for one other point, say X are reduced from 2 to 1.
- More than one operation apart from those for Y itself are reduced from 2 to 1, let us assume X and W have changed from 2 operations to 1.
The first case is similar to meeting at a location which needs 1 operation from each point Y and Z (as mentioned earlier such a point always exists), both give a minimum number of operations equal to 2*N-2.
The second case is same as finding X as a potential meeting point while looking for locations which need Y and X to meet in most 1 operation each (as X is 1 operation away from Y as stated in case 2).
For case 3 also the point Y is discoverable similar to case 2.
Thus the approach we are going to follow covers all potential points that can be chosen as meeting points to minimize the operations.
We have already established that it is possible to equate locations of 2 points (say {a, b}, {c, d}) in at most 2 operations, we can move a point along horizontal, vertical and diagonal lines on the axis, thus we pick a line inclined in one of these directions (namely {0\degree, 45\degree, 90\degree, 135\degree}) for {a, b} to move along, and we pick one of the remaining 3 directions for {c, d} to move along. This way each of them only moves along most 1 of the allowed lines on the axis until it meets with the other thus giving us the location of their meeting with no more than 1 operation each.
Once we choose 2 points, the above mentioned locations of meeting can be found using intersection of line1_{x} - denoting the line through {a, b} inclined at x\degree to the horizontal axis and line2_{y} - denoting the line through {c, d} inclined at y\degree to the horizontal axis, where x\neq y. This yields the following pairs of intersecting lines:
Once we have these potential meeting points, we will traverse through them and for each point P we calculate the sum of operations needed for each of the given points to coincide with P. Minimum of these sums would be our answer.
TIME COMPLEXITY:
O(N\times N\times N) per test case.
Because there can be N\times N potential meeting points and for each of these we will find the sum of operations for N points.
SOLUTIONS:
Setter
#include<bits/stdc++.h>
using namespace std;
template <class T> ostream &operator << (ostream &os, const vector<T> &p) { os << "["; for (auto&it : p) os << it << " "; return os << "]";}
template <class S, class T> ostream &operator << (ostream &os, const pair<S, T> &p) { return os << "(" << p.first << "," << p.second << ")";}
#ifndef ONLINE_JUDGE
#define deb(...) dbs(#VA_ARGS,VA_ARGS)
template <class T> void dbs(string str, T t) { cerr << str << ":" << t << "\n";}
template<class T, class...S> void dbs(string str, T t, S... s) { int idx = str.find(','); cerr << str.substr(0, idx) << ":" << t << ","; dbs(str.substr(idx + 1), s...);}
#else
#define deb(...){}
#endif
#define ld double
#define int long long
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
// deb(x);
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || ( cnt == 19 && fi > 1) ));
} else if (g == endd) {
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
} else {
deb(l, r, x, cnt);
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
#define fi first
#define se second
#define tiii tuple<int, int, int>
#define mt make_tuple
const int maxv = 2e18;
int num(int a, int b) {
return a + rand() % (b - a + 1);
}
tiii cal (int& a, int& b, int& c, int& p, int& q, int& r) {
//program that reads a, b, c, p, q and r. Let ax + by + c = 0 and px + qy + r = 0 be the equations
// of two lines. Print their point of intersection.
int den = a * q - b * p;
int x = maxv, y = 0;
if (den != 0) {
x = b * r - q * c; y = p * c - a * r;
}
return {x, y, den};
}
void solve(int tc) {
int n; cin >> n;
vector<pair<int, int>> a(n);
map<int, int> diff1, diff2, X, Y;
map<pair<int, int>, int> eq;
for (int i = 0; i < n; i++) {
cin >> a[i].first;
}
for (int i = 0; i < n; i++) {
cin >> a[i].second;
eq[ {a[i].first, a[i].second}]++; // counts no of points haveing same (X, Y)
diff1[a[i].first - a[i].second]++; // counts no of points haveing same (X - Y)
diff2[a[i].first + a[i].second]++; // counts no of points haveing same (X + Y)
X[a[i].first]++; // counts no of points haveing same X
Y[a[i].second]++; // counts no of points haveing same Y
}
auto fun = [&](tiii T) {
int x = get<0>(T), y = get<1>(T), d = get<2>(T);
int cur = 2 * n;
if (x == maxv)return cur;
if (x % d == 0)cur -= X[x / d];
if (y % d == 0)cur -= Y[y / d];
if ((x - y) % d == 0)cur -= diff1[(x - y) / d];
if ((x + y) % d == 0)cur -= diff2[(x + y) / d];
if (x % d == 0 && y % d == 0)cur += 2 * eq[ {x / d, y / d}];
return cur;
};
int ans = 2 * n;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int a1 = 1;
int b1 = 0;
int c1 = -a[i].fi;
tiii p;
int a2, b2, c2;
a2 = 0;
b2 = 1;
c2 = -a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
a2 = 1;
b2 = -1;
c2 = -a[j].fi + a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
a2 = 1;
b2 = 1;
c2 = -a[j].fi - a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
a1 = 0;
b1 = 1;
c1 = -a[i].se;
a2 = 1;
b2 = -1;
c2 = -a[j].fi + a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
a2 = 1;
b2 = 1;
c2 = -a[j].fi - a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
a1 = 1;
b1 = -1;
c1 = -a[i].fi + a[i].se;
a2 = 1;
b2 = 1;
c2 = -a[j].fi - a[j].se;
p = cal(a1, b1, c1, a2, b2, c2);
ans = min(ans, fun(p));
}
}
cout << ans << '\n';
}
signed main() {
ios_base :: sync_with_stdio(0); cin.tie(0); cout.tie(0);
int t; cin >> t;
for (int i = 1; i <= t; i++) solve(i);
return 0;
}
Tester
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T& a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T& a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x = 0;
int cnt = 0;
int fi = -1;
bool is_neg = false;
while (true) {
char g = getchar();
if (g == '-') {
assert(fi == -1);
is_neg = true;
continue;
}
if ('0' <= g && g <= '9') {
x *= 10;
x += g - '0';
if (cnt == 0) {
fi = g - '0';
}
cnt++;
assert(fi != 0 || cnt == 1);
assert(fi != 0 || is_neg == false);
assert(!(cnt > 19 || (cnt == 19 && fi > 1)));
}
else if (g == endd) {
assert(cnt > 0);
if (is_neg) {
x = -x;
}
assert(l <= x && x <= r);
return x;
}
else {
//assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert(g != -1);
if (g == endd) {
break;
}
cnt++;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l, r, ' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l, r, '\n');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
struct MT {
int ctr;
int val;
int type;
bool operator<(const MT& other) const
{
return tie(ctr, val, type) < tie(other.ctr, other.val, other.type);
}
bool operator==(const MT& other) const
{
return tie(ctr, val, type) == tie(other.ctr, other.val, other.type);
}
static pair<int, int> intersection(const MT& a, const MT& b)
{
assert(a.type != b.type);
if (a.type == 0)
{
switch (b.type)
{
case 1:
return { a.val, b.val };
case 2:
return { a.val, b.val - a.val };
case 3:
return { a.val, b.val + a.val };
default:
assert(false);
}
}
if (a.type == 1)
{
switch (b.type)
{
case 0:
return { b.val, a.val };
case 2:
return { b.val - a.val, a.val};
case 3:
return { a.val + b.val, a.val};
default:
assert(false);
}
}
if (a.type == 2)
{
switch (b.type)
{
case 0:
return { b.val, a.val - b.val};
case 1:
return { a.val - b.val, b.val };
case 3:
return { (a.val + b.val) / 2, a.val - (a.val + b.val) / 2};
default:
assert(false);
}
}
if (a.type == 3)
{
switch (b.type)
{
case 0:
return { b.val, a.val + b.val };
case 1:
return { a.val + b.val, b.val };
case 2:
return { (a.val + b.val) / 2, b.val - (a.val + b.val) / 2 };
default:
assert(false);
}
}
return { 0, 0 };
}
};
int main(int argc, char** argv)
{
#ifdef HOME
if (IsDebuggerPresent())
{
freopen("../POINTMEE-1.in", "rb", stdin);
//freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
int T = readIntLn(1, 300);
int sumN = 0;
forn(tc, T)
{
int N = readIntLn(2, 200);
sumN += N;
vector<pair<int, int> > w(N);
int idx = 1;
for (auto& wi : w)
{
if (idx == N)
{
wi.first = readIntLn(-1'000'000'000, 1'000'000'000);
}
else
{
wi.first = readIntSp(-1'000'000'000, 1'000'000'000);
}
++idx;
}
idx = 1;
for (auto& wi : w)
{
if (idx == N)
{
wi.second = readIntLn(-1'000'000'000, 1'000'000'000);
}
else
{
wi.second = readIntSp(-1'000'000'000, 1'000'000'000);
}
++idx;
}
sort(w.begin(), w.end());
w.erase(unique(w.begin(), w.end()), w.end());
assert(w.size() == N);
int res = 2 * N;
map<int, int> x, y, xpy, xsy;
set<pair<int, int> > s;
vector<MT> wmt;
for (auto& wi : w)
{
wi.first *= 2;
wi.second *= 2;
s.insert(wi);
x[wi.first]++;
y[wi.second]++;
xpy[wi.first + wi.second]++;
xsy[wi.first - wi.second]++;
}
for(const auto xv : x)
{
wmt.push_back({ xv.second, xv.first, 0 });
}
for (const auto yv : y)
{
wmt.push_back({ yv.second, yv.first, 1 });
}
for (const auto xpyv : xpy)
{
wmt.push_back({ xpyv.second, xpyv.first, 2 });
}
for (const auto xsyv : xsy)
{
wmt.push_back({ xsyv.second, xsyv.first, 3 });
}
sort(wmt.begin(), wmt.end());
reverse(wmt.begin(), wmt.end());
//check all val
// bool all1 = true;
// set<int> sVal;
// forn(i, wmt.size())
// {
// if (sVal.count(wmt[i].val))
// all1 = false;
// sVal.insert(wmt[i].val);
// }
// if (all1)
// {
// printf("%d\n", 2 * N - 2);
// continue;
// }
forn(i, wmt.size())
{
const auto wi = wmt[i];
fore(j, i+1, wmt.size()-1)
{
const auto wj = wmt[j];
if(wi.type == wj.type)
continue;
int bb = 2 * N - (wi.ctr + 3*wj.ctr);
//if(bb >= res)
// break;
const auto wij = MT::intersection(wi, wj);
int xx = wij.first;
int yy = wij.second;
int xppy = wij.first + wij.second;
int xssy = wij.first - wij.second;
int curr = 2 * (N+s.count(wij)) - x[xx] - y[yy] - xpy[xppy] - xsy[xssy];
if (curr < res)
res = curr;
}
}
printf("%d\n", res);
}
assert(sumN <= 600);
assert(getchar() == -1);
return 0;
}
Editorialist
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve() {
int n, ans=0, temp=0;
cin>>n;
int a[n], b[n];
for(int i=0; i<n; i++) {
cin>>a[i];
a[i]*=2;
}
for(int i=0; i<n; i++) {
cin>>b[i];
b[i]*=2;
}
vector<int> x, y;
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
if(i==j) continue;
int a1=a[i], b1=b[i], c=a[j], d=b[j];
x.pb_(a1); y.pb_(d);
x.pb_(c); y.pb_(b1+c-a1);
x.pb_(c); y.pb_(b1-c+a1);
x.pb_(a1+b1-d); y.pb_(d);
x.pb_(a1-b1+d); y.pb_(d);
x.pb_((a1+b1+c-d)/2); y.pb_((b1+a1-c+d)/2);
// if you were to run the loop from i+1,
//you'd have to insert the following into x and y too:
// x.pb_(c); y.pb_(b1);
// x.pb_(a1); y.pb_(d+a1-c);
// x.pb_(a1); y.pb_(d-a1+c);
// x.pb_(c+b1-d); y.pb_(b1);
// x.pb_(c-b1+d); y.pb_(b1);
// x.pb_((a1-b1+c+d)/2); y.pb_((b1-a1+c+d)/2);
}
}
for(int i=0; i<x.size(); i++) {
temp=0;
int top=y[i], right=x[i];
for(int j=0; j<n; j++) {
if(right==a[j] && top==b[j]) temp+=0;
else if(right==a[j] || top==b[j]) temp++;
else if(abs(right-a[j])==abs(top-b[j])) temp++;
else temp+=2;
}
if(i==0) ans=temp;
else ans=min(temp, ans);
}
cout<<ans<<endl;
}
int32_t main()
{
int t=1;
cin>>t;
while(t--) {
solve();
}
}