PROBLEM LINK:
Setter- Erfan Alimohammadi
Tester- Roman Bilyi
Editorialist- Abhishek Pandey
DIFFICULTY:
MEDIUM
PRE-REQUISITES:
Convex Hull, Geometry, Handling Corner Cases.
PROBLEM:
Given the co-ordinates of Police and Thieves respectively, how many more Police officers are needed to enclose all thieves in a convex hull.
QUICK-EXPLANATION:
Key to AC- Realize that the answer is never more than 3! Now all that is left is case work.
The first thing to observe is that the answer can never be greater than 3. This is because the problem does not impose any constraints for the value of co-ordinates to be in any prescribed range/limit. Hence, it is always possible to place co-ordinates very, very far away to make a very big triangle enclosing everyone.
Now, ans is 0 if the police already enclose all the thieves. This can be easily checked by making a convex hull of both police and thieves, and making sure no thief lies of the edge or vertex (because if it is so, then by definition of convex hull the thief must be inside).
Similarly, the case of 3 is easy to see - Possible if no police officer lies on the hull!
Now, to decide whether the answer is 1 or 2, depends on if we can find a contiguous subset of police officers on the hull (take as many as possible), such that there are >1 police officers in it and the lines from it to the adjacent thieves converge or diverge. (Recall that we took as many police officers in the contiguous subset as possible - so this means that the vertex before the first police officer and vertex after the last police officer are thieves!)
EXPLANATION:
We will discuss answer for each case. separately, so it is easier for you to read only the relevant parts ![]()
1. When answer is 0-
Clearly, this is possible if the convex hull of police officers already encloses the thieves. But wait, how do we do it? Making a polygon and checking if a point lies inside it or not will be O(N^2) and hence will time out!!
We need to use the definition of convex hull here ![]()
If we make a convex hull using both, points of police and thief - then any thief not lying on edge or vertex of the convex hull MUST lie strictly inside it (according to the very definition of convex hull!)!! And now we can iterate over the points in hull in linear time and solve this case!
When the answer is 3-
After seeing above argument for case 0 (or perhaps reading the quick explanation ![]() ), you might have already guessed how to do this part.
), you might have already guessed how to do this part.
Make a convex hull using both thieves and police, and check any police lies on the vertices (remember - if its not a police on the vertex, then its a thief!). A police officer lying on edge does not help in reducing the answer (Why?), so it will be good to make a new convex hull (just for this case) to include points only at vertices of the hull.
Once our hull is set, we check all vertices of it. If their are thieves at all of them, then the answer is 3 as the thieves “enclose” the police (any enclosed officer cannot be part of final, enclosing hull!)
3. When answer is 1 or 2-
This section is left as an exercise to the reader. Have fun!!! ![]()
.
.
.
.
.
.
.
Had fun? Good!
This is easier to explain with a picture, so look at the image below (ALL credits to images go to our lovely tester @romawhite - Kudos to him for being such a sweetheart!)
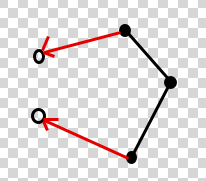
This is image of a case where the answer is 1. The black dots are Police Officers, and the hollow dots are thieves. Look at the red vectors! Looking at the image, we can say that-
"If red vectors converge, then we can place a police officer at some far away distance point to get answer as 1. Else, since ans \leq 3 and we already checked the cases for 0,1,3, then the answer is 2. "
Alternatively-
“If the red vectors converge, then the answer is 1, else if they diverge the answer is 2.”
To make the case for Ans=2 more clear, refer to image below (which is made by our lovely tester @romawhite !!)
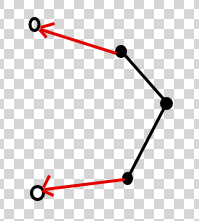
Now, easy to say, but how to check it?
Lets go step by step! The first part is to iterate through the hull, and group the contiguous police officers on hull together. Now, for every such group, realize that the points adjacent to this group are thieves, else they’d also be a part of group! Keep track of starting and end points of the group, and Voila! We are able to get the red vectors in image!!
How to proceed after getting them? Simple! Converging, or Diverging can be checked by sign vector product! Depending on how you define things in your implementation, positive sign will mean one thing and negative sign will mean the other. You can verify that the signs will be opposite by apply thumb-rule on various examples!
Now, what if I ask you how many signs are there? 1?\ 2? \ 0.5?
All of above are wrong! Consider 3 signs for this problem - positive, negative, and zero! What to do if the sign is 0? How will be handle the case if these vectors are parallel?
Vector product being 0 means that the vectors are parallel or anti parallel. Realize that this can also happen if there is a thief on edge of the convex hull!
First, check if they are parallel or anti parallel using the scalar product. If they are antiparallel, its easy to see that this means that the thief is on the edge of the hull! Answer for this case is 1. However, if they are parallel, then the answer is 2.
Ultimately, remember that you can place an officer at a very, very far away position. Hence you only need one favorable group, which, if included in the hull along with the newly placed officer, would contain all the thieves inside! This means, that, if even 1 good grouping exists for which answer is 1, the final answer is 1 as we can make a hull using that group and place 1 officer at a very far, far place! If there is no such grouping, the answer is 2
But wait a minute…doesn’t something feel weird??? How did we solve a geometry problem without getting stuck at some damn corner cases? Turns out, there are corner cases to handle!!
Look at the below case-
1
3 1
10 0
10 6
10 10
10 5
The police officer, and the thieves all lie on the same straight line X=10. On a closer inspection, you will realize that this satisfies our conditions for Ans=1. But if you see closely, the answer has to be 2 as otherwise the thief lies on the edge which is not allowed!! Then what?
Before declaring the answer to be 1, additionally check for this case, that if all police officers ar lying on the same line. I’d recommend you to look at tester’s code for the implementation details ![]()
Once we take care of all of above, we have checked off another problem from our TODO list!
SOLUTION
Tester (Romawhite)
#include "bits/stdc++.h"
using namespace std;
#define FOR(i,a,b) for (int i = (a); i < (b); i++)
#define RFOR(i,b,a) for (int i = (b) - 1; i >= (a); i--)
#define ITER(it,a) for (__typeof(a.begin()) it = a.begin(); it != a.end(); it++)
#define FILL(a,value) memset(a, value, sizeof(a))
#define SZ(a) (int)a.size()
#define ALL(a) a.begin(), a.end()
#define PB push_back
#define MP make_pair
typedef long long Int;
typedef vector<int> VI;
typedef pair<int, int> PII;
const double PI = acos(-1.0);
const int INF = 1000 * 1000 * 1000;
const Int LINF = INF * (Int) INF;
const int MAX = 307;
const int MOD = 998244353;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
void assertEof(){
assert(getchar()==-1);
}
struct Point{
int x;
int y;
int type;
bool operator<(const Point& p)const {
return MP(x, y) < MP(p.x, p.y);
}
};
Int vmult(Int x1, Int y1, Int x2, Int y2)
{
return x1 * y2 - x2 * y1;
}
Int scmult(Int x1, Int y1, Int x2, Int y2)
{
return x1 * x2 + y1 * y2;
}
vector<Point> convex_hull(vector<Point> A, bool on_edge) {
sort(ALL(A));
vector<Point> U, D;
U.push_back(A[0]);
D.push_back(A[0]);
FOR(i,1,SZ(A))
{
while (SZ(U) >= 2)
{
Int vm = vmult(U.back().x - U[SZ(U) - 2].x, U.back().y - U[SZ(U) - 2].y, A[i].x - U.back().x, A[i].y - U.back().y);
if (vm < 0 || (vm == 0 && !on_edge))
{
U.pop_back();
}
else
{
break;
}
}
U.push_back(A[i]);
}
FOR(i,1,SZ(A))
{
while (SZ(D) >= 2)
{
Int vm = vmult(D.back().x - D[SZ(D) - 2].x, D.back().y - D[SZ(D) - 2].y, A[i].x - D.back().x, A[i].y - D.back().y);
if (vm > 0 || (vm == 0 && !on_edge))
{
D.pop_back();
}
else
{
break;
}
}
D.push_back(A[i]);
}
RFOR(i,SZ(D) - 1, 1)
U.push_back(D[i]);
return U;
}
int main(int argc, char* argv[])
{
// freopen("in.txt", "r", stdin);
//ios::sync_with_stdio(false); cin.tie(0);
int t = readIntLn(1, 10);
FOR(tt,0,t)
{
int n = readIntSp(0, 100000);
int m = readIntLn(1, 100000);
vector<Point> A;
FOR(i,0,n)
{
int x = readIntSp(-200000000, 200000000);
int y = readIntLn(-200000000, 200000000);
A.emplace_back(Point{x, y, 0});
}
FOR(i,0,m)
{
int x = readIntSp(-200000000, 200000000);
int y = readIntLn(-200000000, 200000000);
A.emplace_back(Point{x, y, 1});
}
vector<Point> B = convex_hull(A, false);
vector<Point> C = convex_hull(A, true);
bool ok = true;
FOR(i,0,SZ(C))
{
if (C[i].type == 1)
ok = false;
}
if (ok)
{
cout << 0 << endl;
continue;
}
ok = true;
FOR(i,0,SZ(B))
{
if (B[i].type == 0)
ok = false;
}
if (ok)
{
cout << 3 << endl;
continue;
}
int ans = 2;
int l = -1;
ok = false;
FOR(i,0,2 * SZ(C))
{
int id = i % SZ(C);
if (C[id].type == 0)
{
if (l == -1) {
l = id;
ok = false;
}
else {
Int x1 = C[(l + 1) % SZ(C)].x - C[l].x;
Int y1 = C[(l + 1) % SZ(C)].y - C[l].y;
Int x2 = C[id].x - C[l].x;
Int y2 = C[id].y - C[l].y;
if (vmult(x1, y1, x2, y2) != 0)
ok = true;
}
}
else
{
if (l != -1)
{
int r = (id - 1 + SZ(C)) % SZ(C);
Int x1 = C[(l - 1 + SZ(C)) % SZ(C)].x - C[l].x;
Int y1 = C[(l - 1 + SZ(C)) % SZ(C)].y - C[l].y;
Int x2 = C[id].x - C[r].x;
Int y2 = C[id].y - C[r].y;
if (vmult(x1, y1, x2, y2) > 0 || (ok && vmult(x1, y1, x2, y2) == 0 && scmult(x1, y1, x2, y2) < 0))
ans = 1;
}
l = -1;
}
}
cout << ans << endl;
}
assertEof();
cerr << 1.0 * clock() / CLOCKS_PER_SEC << endl;
}
Tester(Hasan)
#include <iostream>
#include <algorithm>
#include <string>
#include <set>
#include <map>
#include <assert.h>
using namespace std;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
assert(cnt>0);
if(is_neg){
x= -x;
}
if(!(l<=x && x<=r)){
cerr<<l<<" "<<r<<" "<<x<<endl;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
int T;
int n;
int m;
set<pair<int,int>> hh;
struct p{
long long x,y,t;
};
bool operator<(p a, p b){
if(a.x == b.x){
return a.y<b.y;
}
return a.x<b.x;
}
p arr[200200];
long long cross(long long x1,long long y1,long long x2,long long y2){
return x1 * y2 - x2 * y1;
}
long long is_left(p a, p b, p c){
return cross(b.x-a.x,b.y-a.y,c.x-b.x,c.y-b.y) > 0;
}
long long is_right(p a, p b, p c){
return cross(b.x-a.x,b.y-a.y,c.x-b.x,c.y-b.y) < 0;
}
p upper[200200];
p lower[200200];
p pol[200200];
int up=0,lw=0,pn=0;
int main(){
//freopen("2.in.txt","r",stdin);
//freopen("input.txt","w",stdout);
T=readIntLn(1,10);
for(int iii=0;iii<T;iii++){
/*if(iii==6){
cout<<1<<endl;
n=readIntSp(0,100000);
m=readIntLn(1,100000);
cout<<n<<" "<<m<<endl;
for(int i=0;i<n;i++){
int x,y;
x=readIntSp(-1000000000,1000000000);
y=readIntLn(-1000000000,1000000000);
cout<<x<<" "<<y<<endl;
}
for(int i=0;i<m;i++){
int x,y;
x=readIntSp(-1000000000,1000000000);
y=readIntLn(-1000000000,1000000000);
cout<<x<<" "<<y<<endl;
}
return 0;
}*/
hh.clear();
n=readIntSp(0,100000);
m=readIntLn(1,100000);
up=lw= 0;
for(int i=0;i<n;i++){
int x,y;
x=readIntSp(-1000000000,1000000000);
y=readIntLn(-1000000000,1000000000);
assert(hh.count(make_pair(x,y)) == 0);
hh.insert(make_pair(x,y));
arr[i].x = x;
arr[i].y = y;
arr[i].t = 1;
}
for(int i=0;i<m;i++){
int x,y;
x=readIntSp(-1000000000,1000000000);
y=readIntLn(-1000000000,1000000000);
assert(hh.count(make_pair(x,y)) == 0);
hh.insert(make_pair(x,y));
arr[n+i].x = x;
arr[n+i].y = y;
arr[n+i].t = 2;
}
sort(arr,arr+n+m);
for(int i=0;i<n+m;i++){
if(arr[i].t == 2){
i=i;
}
while(up>=2 && !is_right(upper[up-2],upper[up-1],arr[i])){
up--;
}
while(lw>=2 && !is_left(lower[lw-2],lower[lw-1],arr[i])){
lw--;
}
upper[up++]=arr[i];
lower[lw++]=arr[i];
}
bool all_police=true,all_theif=true;
for(int i=0;i<up;i++){
if(upper[i].t == 1)all_theif=false;
}
for(int i=0;i<lw;i++){
if(lower[i].t == 1)all_theif=false;
}
if(all_theif){
cout<<3<<endl;
continue;
}
up=lw= 0;
for(int i=0;i<n+m;i++){
if(arr[i].t == 2){
i=i;
}
while(up>=2 && is_left(upper[up-2],upper[up-1],arr[i])){
up--;
}
while(lw>=2 && is_right(lower[lw-2],lower[lw-1],arr[i])){
lw--;
}
upper[up++]=arr[i];
lower[lw++]=arr[i];
}
for(int i=0;i<up;i++){
if(upper[i].t == 2)all_police=false;
}
for(int i=0;i<lw;i++){
if(lower[i].t == 2)all_police=false;
}
if(all_police){
cout<<0<<endl;
continue;
}
pn=0;
for(int i=0;i<up-1;i++){
pol[pn++]=upper[i];
}
for(int i=lw-1;i>=1;i--){
pol[pn++]=lower[i];
}
bool found=false;
/*for(int i=0;i<pn;i++){
int a=i,b=(i+1)%pn,c=(i+2)%pn,d=(i+3)%pn;
if(pol[b].t != 1)continue;
if(pol[c].t != 1)continue;
p third ;
third.x = pol[a].x + (pol[c].x - pol[b].x);
third.y = pol[a].y + (pol[c].y - pol[b].y);
if(is_right(pol[d],pol[c],third)){
found
}
}*/
int cur=0;
for(int i=0;i<pn;i++){
if(pol[i].t != 1){
if(cur == i){
cur =(cur + 1)%pn;
}
continue;
}
while(pol[cur].t == 1){
cur = (cur+1)%pn;
}
int a=(i+pn-1)%pn,b=i,c=(cur+pn-1)%pn,d=cur;
p third ;
third.x = pol[a].x + (pol[c].x - pol[b].x);
third.y = pol[a].y + (pol[c].y - pol[b].y);
if(is_right(pol[d],pol[c],third)){
found=true;
}
if(cur == i){
cur =(cur + 1)%pn;
}
}
if(found){
cout<<1<<endl;
} else {
cout<<2<<endl;
}
}
assert(getchar()==-1);
}
Time Complexity=O((N+M)Log(N+M))
Space Complexity=O((N+M)Log(N+M))
CHEF VIJJU’S CORNER 
For ans=3 case, why police on edges do not help
They are surrounded by, or enclosed by thieves on both sides! Its not possible for this police to be part of the final, enclosing hull because thieves on vertices are considered outside!!
Having Trouble Debugging?
- Dont forget that the points can be collinear - this can cause some convex hull algorithms to fail!
- Make sure to avoid some ugly geometry stuff like Ray Intersection etc. as it can get ugly pretty fast!
- Modularize the code!! Then find that which part of it is failing! A clean implementation helps a LOT in debugging!!
- Be cautious of overflows! And precision issues if using double etc!!
- Dont forget that all operations, except for case Ans=3, are done of such a hull which allows points between vertices, i.e. on the edges!!