PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Contest: Division 4
Author:
Tester: sushil2006
Editorialist: iceknight1093
DIFFICULTY:
Medium
PREREQUISITES:
None
PROBLEM:
Given N, solve the following problem for each K = 0, 1, 2, \ldots, N:
- Construct a polygon with at most 150 vertices, all of which have integer coordinates in [0, 10^4], such that exactly K unordered pairs of edges of the polygon intersect non-trivially.
Two edges intersect non-trivially if their intersection is a single point that’s not an endpoint of either edge.
EXPLANATION:
The number of vertices we’re allowed is 150, which is in general much smaller than the number of intersections we want.
In particular, note that with X vertices, we can have at best \frac{X\cdot (X-1)}{2} - X pairs of intersections: all pairs, minus adjacent edges.
For X = 150 this value is a bit over 11000, which is quite close to the upper limit of N = 10^4.
So, we definitely need to be able to come up with a configuration where almost all pairs of segments intersect.
One way to do that, is to utilize a circle.
Consider a circle with some 2M points marked on its diameter (for now, assume they’re equidistant).
Now, look at the following edges:
- For each 1 \leq i \leq M, the edge (i, i+M).
- For each 1 \leq i \lt M, the edge (i, i+M+1).
- To close the polygon, the edge (M, M+1).
If you try drawing this out, you’ll notice that nearly all pairs of these edges intersect each other - we’ll have close to 2M^2 intersections; in fact something along the lines of 2M^2 - 5M or so, which is quite close to optimal.
One issue here is that vertices on the circle might not have integer coordinates, but that’s easy to remedy: note that the circle wasn’t really necessary, just 2M points placed appropriately so that the edges created this way intersect.
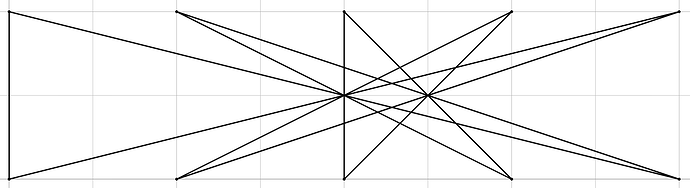
For example, one alternative is to create two rows of M points each, label them 1 to 2M in clockwise order, and then use the same construction of edges: this gives us the same intersections.
This looks like the following figure, for M = 5:
For a fixed target K, suppose we perform this construction with the largest possible M we can, while ensuring that the number of intersections created is \leq K.
Let the current value of M be M_0.
Since 2\cdot 72^2 - 5\cdot 72 \gt 10^4, we’ll definitely use at most 2\cdot 71 = 142 vertices here, meaning there will be a few leftover - at least 8 for sure.
We then require a handful more intersections to reach exactly K.
Let’s bound this extra a bit.
We know that M_0 + 1 didn’t work for us, i.e. 2(M_0+1)^2 - 5(M_0+1) \gt K.
This tells us that the number of extra intersections needed is less than 4M_0 - 3, which is quite nice because we already have around 2M_0 edges to intersect with.
For example, one way to finish is as follows.
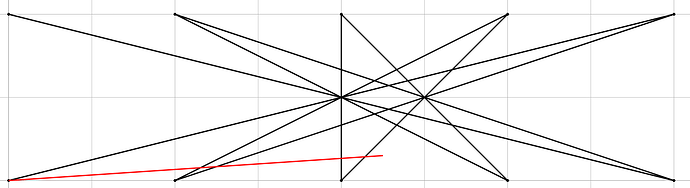
Delete the leftmost vertical edge to “open up” the polygon.
Now, from the bottom-left vertex, we can easily create upto (2M_0 - 2) intersections by starting a new edge there and directing it up-right a bit, limiting its length as needed.
This would look like the red segment below:
Similarly, we can create another (2M_0 - 2) intersections from the top-left vertex by starting
an edge there and directing it down-right a bit.
To ensure that the coordinates are integers, you can play around with the scaling a bit: create enough vertical and horizontal space between the points and there’ll be no problem; coordinates aren’t an issue because we have only \approx 70 points in each row so they can be spaced out nicely within 10^4.
Note that creating an even number of intersections this way is safe, since you won’t be “inside” the polygon and can just use a couple more edges to close out the polygon without creating any more intersections.
If you want to create an odd number of intersections a little more care is needed, but it’s not too hard from here either: a simple solution is to just create one less intersection than needed (so it becomes even), and then create the last intersection somewhere outside while closing out the polygon.
This uses at most two more vertices to end up in a situation where either 0 or 1 more intersection is needed.
We still have at least 6 vertices free to close out the polygon and maybe create another intersection, which is not too hard to do.
TIME COMPLEXITY:
\mathcal{O}(N\sqrt N) per testcase.
CODE:
Author's code (C++)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define all(c) ((c).begin()), ((c).end())
#define sz(x) ((int)(x).size())
#ifdef LOCAL
#include <print.h>
#else
#define trace(...)
#define endl "\n" // remove in interactive
#endif
struct PT {
ll x, y;
PT(int x, int y) : x(x), y(y) {}
PT operator + (const PT &p) const { return PT(x+p.x, y+p.y); }
PT operator - (const PT &p) const { return PT(x-p.x, y-p.y); }
PT operator * (long long c) const { return PT(x*c, y*c ); }
};
// code to print a point with << operator
ostream& operator<<(ostream& os, const PT& p) {
return os << "(" << p.x << ", " << p.y << ")";
}
long long cross(PT p, PT q) { return p.x*q.y-p.y*q.x; }
bool SegmentsIntersectProperly(PT a, PT b, PT c, PT d){
// if(LinesParallel(a, b, c, d)) return false;
ll C1 = cross(d-a, b-a), C2 = cross(c-a, b-a);
if(C1 * __int128_t(C2) >= 0){
// trace(C1, C2);
return false;
}
// if (cross(d-a, b-a) * __int128_t(cross(c-a, b-a)) >= 0)return false;
ll C3 = cross(a-c, d-c), C4 = cross(b-c, d-c);
if (C3 * __int128_t(C4) >= 0){
// trace(C3, C4);
return false;
}
// if (cross(a-c, d-c) * __int128_t(cross(b-c, d-c)) >= 0) return false;
return true;
}
vector<PT> getGadget(int k, PT p){
if(k == 1) return {p, p + PT(0, 1) * 2};
vector<PT> res = {p, p + PT(k-1, 1) * 2};
for(int i = 1; i < k; i++){
res.push_back(p + PT(i, 0) * 2);
res.push_back(p + PT(k - 1 - i, 1) * 2);
}
return res;
}
int farthest = 0;
const int INF = 1e4;
int maxn = 0;
vector<PT> construct(int k, bool dbg = false){
int K = k;
if(k == 0) return {PT(0, 0), PT(0, 1), PT(1, 1)};
const int O = 500;
PT p(O, O);
int max_nint = 0;
// while(k > 0){
int t = 2;
while(((2 * t - 2) * (2 * t - 3)) / 2 <= k) t++; t--;
k -= ((2 * t - 2) * (2 * t - 3)) / 2;
int closest = k;
vector<PT> res = getGadget(t, p);
if(k >= 2 * t - 2){
k -= 2 * t - 2;
res.push_back(PT(O + 2 * t, O));
for(int x = O - 1; x <= O + 2 * t - 1; x += 2){
PT here = PT(x, O + 2);
int num_intersections = 0;
for(int i = 0; i < sz(res) - 1; i++){
if(SegmentsIntersectProperly(res[i], res[i+1], res.back(), here)){
num_intersections++;
}
if(num_intersections > k) break;
}
if(num_intersections <= k) closest = min(closest, k - num_intersections);
if(num_intersections >= k - 1 && num_intersections <= k){
k -= num_intersections;
res.push_back(here);
res.push_back(PT(O - 10, O + 3));
if(k) res.push_back(PT(O - 10, O + 4));
return res;
}
}
} else{
// if(dbg) cerr << 2 * t << " " << k << endl;
for(int x = O - 1; x <= O + 2 * t - 1; x += 2){
PT here = PT(x, O);
int num_intersections = 0;
for(int i = 0; i < sz(res) - 1; i++){
if(SegmentsIntersectProperly(res[i],res[i+1], res.back(), here)){
num_intersections++;
}
if(num_intersections > k) break;
}
if(num_intersections <= k) closest = min(closest, k - num_intersections);
if(num_intersections >= k - 1 && num_intersections <= k){
k -= num_intersections;
res.push_back(here);
res.push_back(PT(O - 4, O - 1));
if(k) res.push_back(PT(x > O ? O - 3: O - 5, O - 1));
return res;
}
}
}
assert(false);
return res;
}
int main(){
ios_base::sync_with_stdio(false);
int K;
cin >> K;
for(int i = 0; i <= K; i++){
vector<PT> polygon = construct(i);
cout << sz(polygon) << endl;
for(auto &pt : polygon){
cout << pt.x << " " << pt.y << endl;
}
}
// trace("Farthest:", farthest);
// trace(maxn);
}