POSTMAN - Editorial

editorial
1

PROBLEM LINK:

Practice
Author: (codechefnitj | CodeChef User Profile for Codechef NITJ Chapter | CodeChef)
Editorialist: CodeChefNITJ

DIFFICULTY:

MEDIUM

PREREQUISITES:

dfs, Euler Tree Traversal, intime, outime

PROBLEM:

if there is a path from house 1 to any other house such that every house in the list either lies on that path or has a distance of 1 from any other house lying on the path

EXPLANATION:

Here firstly we need to observe the structure carefully:

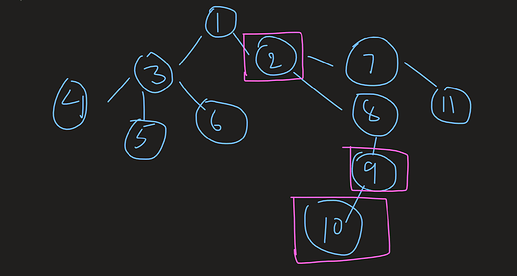
Untitled
Untitled1338×716 85.6 KB

Let us assume we have a list as [2,9,10] and need to move from 1 to all these houses.
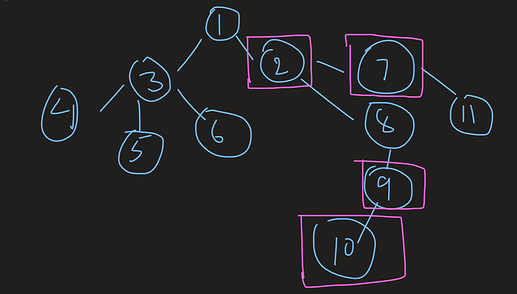
Firstly let us find the deepest node which is 10 here. We can see 10 is in the subtree of each node [2,9]. If we could somehow prove that the deepest node is in the subtree of each other nodes. Then we may say that there is a path from 1 to the deepest node while passing through all other nodes.(Why?)

But here’s a problem:

Untitled
Untitled1243×709 103 KB

here 10 is not in the subtree of 7, but the answer will be "Yes".
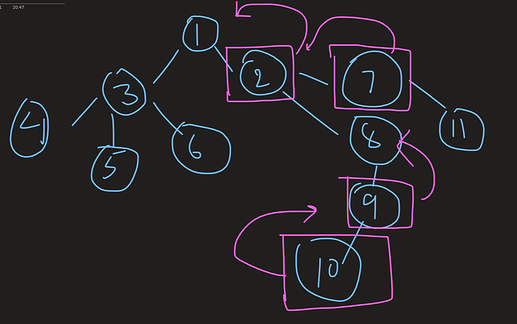
To counter the problem of one unit distance what we shall do is change each node = parent[node].After this we can easily apply subtree idea and get our answer.

Untitled
Untitled1184×744 105 KB

structure after this shall be:

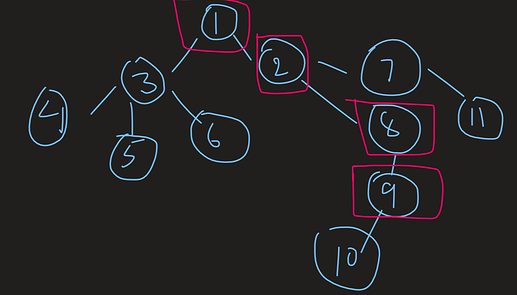
Untitled
Untitled1184×677 87.9 KB

Now we are just left to somehow find if the deepest node is in subtree of other nodes.

To do that we shall user euler tree tour technique with intime and outime arrays and it will help us to find subtree thing.

You can also refer given video to understand this:

TIME COMPLEXITY:

each query takes O(k) time and there are q queries thus so the time complexity will be O(q*k)

SOLUTIONS:

Editorialist's Solution 
#include <bits/stdc++.h>
//#include <boost/multiprecision/cpp_int.hpp>
//using namespace boost::multiprecision;
using namespace std;
#define ll long long int
//#define bint cpp_int
#define pii pair<int, int>
#define mod 1000000007
#define REP(i, a, b) for (int i = a; i < b; i++)
#define maxN 200001
#define all(x) (x).begin(), (x).end()
//int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
//int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
//int dx[] = {-1, 0, 1, 0, 1, -1, 1, -1};
//int dy[] = {0, -1, 0, 1, -1, -1, 1, 1};

vector<int> arr[maxN];
int parent[maxN], n;
int depth[maxN];
int intime[maxN], outime[maxN], timer;

void dfs(int node = 1, int par = 0, int d = 0)
{
    parent[node] = par;
    depth[node] = d;
    intime[node] = ++timer;

    for (int child : arr[node])
    {
        if (child == par)
            continue;

        dfs(child, node, d + 1);
    }

    outime[node] = ++timer;
}

bool isAnces(int par, int node)
{
    return intime[par] <= intime[node] && outime[par] >= outime[node];
}

bool query()
{
    int k, d = -1, node = 0, dum;
    vector<int> vec;

    cin >> k;

    REP(i, 0, k)
    {
        cin >> dum;
        vec.push_back(dum);

        if (d < depth[dum])
            d = depth[dum], node = dum;
    }

    for (int &e : vec)
    {
        if (e != node && parent[e] > 0)
        {
            e = parent[e];
        }
    }

    bool flag = true;

    for (int e : vec)
    {
        flag &= isAnces(e, node);
    }

    return flag;
}

void solve()
{
    int m, a, b;

    cin >> n >> m;

    REP(i, 0, n - 1)
    {
        cin >> a >> b;
        arr[a].push_back(b), arr[b].push_back(a);
    }

    dfs();

    while (m--)
    {
        if (query())
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
}

int main(int argc, char const *argv[])
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int t = 1;

    // cin >> t;

    while (t--)
    {
        solve();
    }

    return 0;
}