Postman intern question

help
#1

1_
1_720×619 51.1 KB
1___
1___707×617 31.8 KB
1_____
1_____705×630 29.5 KB
1_1
1_1703×624 39.1 KB

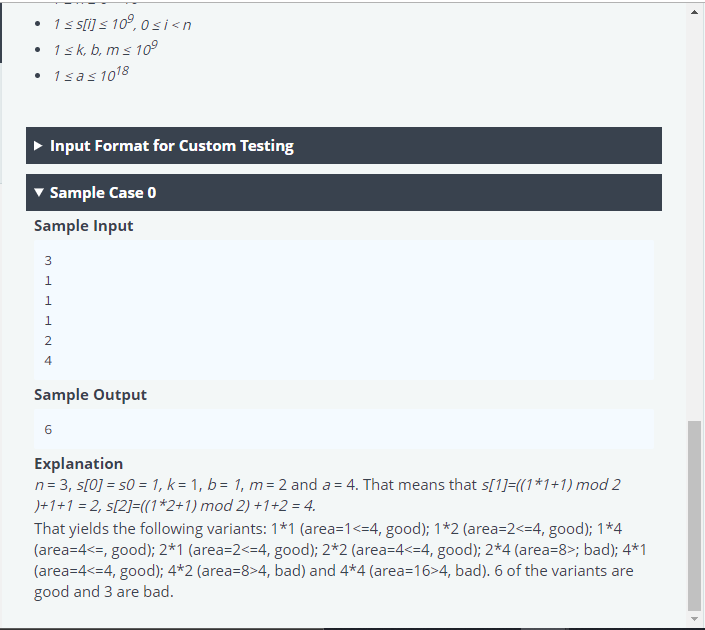
my code:
#define ll long long int
vector s;
long variantsCount(int n, int s0, int k, int b, int m, long a) {

 s.push_back(s0);

for(ll i=1;i<n;i++) 
    s[i] = ((k%m*s[i-1]%m)%m + b%m)%m + 1 + s[i-1];
    
ll lo=0,hi=n-1;
ll cnt=0;

while(lo<=hi) {
    if(s[lo]*s[hi] <= a) {
        cnt+=2*(hi-lo+1) -1;lo++;
    } else {
        hi--;
    }
}

return cnt;

}// only function part

But it does not work on most solutions. Can anyone help?

1 Like
#2

I passed 7 test cases and did all other mcq’s and program still couldn’t make it to the cut off list it is just a scam don’t waste your time.

2 Likes
#3

Nothing is scam. They selected all the candidates scoring near to full marks and there were many of them.

6 Likes
#4

Good luck. lol

#5

Yeah couldn’t solve this one

1 Like
#6

nothing is spam bro, they interviewed those guys who scored full in the coding part as well as whose most MCQ’s were correct.

#7

I gave the same test more than a week ago. I completely solved all the programming questions and I am sure that I have correctly answered most of the MCQs. But till now I didn’t get any mail from them.

#8

I recieved rejection mail within 4 hours, btw can you guys tell the approach for this question

1 Like
#9

Can you help me in solving out this question?

#11

Please help me in solving this question

#12

Solution or hint please

#13

I solved this using two pointers technique. It was medium level question that must be solved in O(n).

#14

But I am unable to implement that in O(n). Any hint?

#15

I solved all the problem there were 3 of them including this Configuration System too. and all the mcq still I was not selected. They mailed me the result in 30 minutes only. On asking the reason they said sorry we can’t disclose. Its because they have already hired the interns and might be not looking for it.

#16

I just need the approach to upsolve this problem for knowledge only bczz the contest is over

#17

The array generated using the formula given in the question will be sorted automatically. So no need to sort it again, otherwise you will get memory limit exceed verdict.
Take two pointers, first in the beginning and other in the end. Let them be start and end. For every start position, find the position of end pointer such that arr[start] * arr[end] <= area.
Here is the pseudocode:

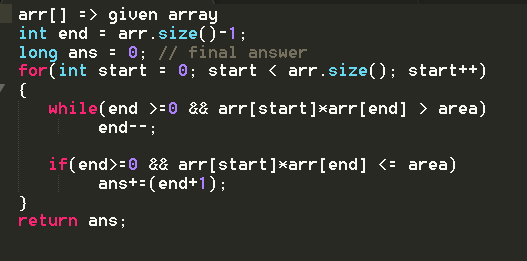
image

#18

Damn, thanks for the algo !

#19

Thanks a lot

#20

Can you give some hints for this question?
Trying for last two days

1
1788×652 64.3 KB
2

#21

Hint: Use DP. States would be: current position, number of bars left, last-placed bar

Solution:
Code complexity (N^2)*(B) = 10^8. A better solution might be available.

	public static long solve(int idx, int b, long[] arr, long xor, int len, int last, long[][][] dp) {
		if (idx == arr.length) {
			if (b == 0) {
				return xor * (len - 1); // final segment value
			} else {
				return Long.MAX_VALUE; // invalid state
			}
		}

		// dp[idx][b][last] is the minimum value you can get from segment
		// [idx,arr.length] when you have 'b' bars to place and the last bar was place
		// placed at index 'last'
		
		if (dp[idx][b][last] != -1) {
			return dp[idx][b][last];
		}
		
		
		long placeBar = Long.MAX_VALUE;
		if (b > 0) {
			long myVal = (xor ^ arr[idx]) * len;
			long restVal = solve(idx + 1, b - 1, arr, 0, 1, idx, dp);
			if (restVal != Long.MAX_VALUE) {
				placeBar = myVal + restVal;
			}
		}
		long notPlaceBar = solve(idx + 1, b, arr, xor ^ arr[idx], len + 1, last, dp);

		return dp[idx][b][last] = Math.min(placeBar, notPlaceBar);
	}