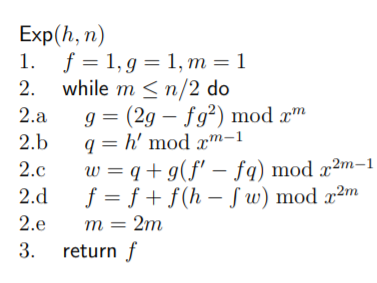PROBLEM LINK:
Author: Ildar Gainullin
Tester: Felipe Mota
Editorialist: Rajarshi Basu
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Generating Functions, FFT
PROBLEM:
In your house, you have a lot of integers. These integers are coloured by Q colours (numbered 1 through Q). For each valid i, you have b_i integers with colour i and each of these integers has value a_i.
For each integer i such that 1 \le i \le N, you need to find the number of different partitions of i. Here, a partition of i consists of one or more integers from your house such that the sum of values of these integers is equal to i. Two partitions are different if there is a colour such that the number of integers with this colour in one partition is different from the number of integers with this colour in the other partition. Since these numbers could be very big, compute them modulo 998,244,353.
Constraints:
- N,Q \leq 150000
EXPLANATION:
Motivation towards intended solution
Let’s jump for the full solution. One initial attempt might be to use dp, maybe with some optimisation? But it will quickly turn out that it’s very difficult to come up with a DP solution. Rather, a much better strategy in problems where we are told that \sum_{}^{} a_i = k for some array a[.] and k, is to approach it using Generating Functions. Maybe try with this in mind?
A slightly different problem
Usually, when we try to solve a ‘Simpler’ instance, we set some of the constraints to 0 or 1. Well, in this case we can set \forall i, b_i = 1. And solve it. But a better scenario is trying setting \forall i, b_i = \infty . Although we might not be able to compute this fast, we will get some vital insights into the problem.
Solution For this Simple problem
In short, let’s say we are trying to answer how many combinations are there such that \sum a_i*b_i = n for some value of n. Then, the solution for this is the coefficient of X^n in (1 + X^{a_1} + X^{2a_1} + X^{3a_1} + \dots)*(1 + X^{a_2} + X^{2a_2} + X^{3a_2} + \dots)*(1 + X^{a_3} + X^{2a_3} + X^{3a_3} + \dots)* \dots*(1 + X^{a_q} + X^{2a_q} + X^{3a_q} + \dots). We denote this as [X^n]\prod_{i}(\sum_{j=0}^{\infty} X^{ja_i}). Hence, to answer all values of n \in \{1,2,3 \dots N\}, we just need to find the first N coefficients. Looks like we are getting somewhere right?
Do note that although we get a very compact equation, this may not be very straightforward to solve.
Reducing our problem
Now, our problem gives us some upper bounds on the b_i s, which make writing a nice formal power series to represent it, harder. However, what if we could try changing it to some combination infinite series again \dots
Solution
The key is to write (1 + X^{a_i} + X^{2a_i} + \dots + X^{b_ia_i}) as \sum_{j=0}^{\infty}X^{ja_i} - \sum_{j=b_i+1}^{\infty}X^{ja_i} . We can quickly show that the above expression can be written as \frac{1-X^{(b_i+1)a_i}}{1-X^{a_i}}. Thus, what we now have to find is [X^n] \prod_{i} \frac{1-X^{(b_i+1)a_i}}{1-X^{a_i}}. Note that here we have used the identity (1+X+X^{a} + X^{2a} + X^{3a} + \dots) = \frac{1}{1-X^a}.
The critical step
Take the natural logarithm!
We use the following identity:
- \ln (1-X^a) = - \sum_{j=0}^{\infty}\frac{X^{j*a}}{j} \dots \dots (1)
- The key point here is that for a particular a_i, there are only \frac{n}{a_i} non-zero terms with exponent less than N.
Lets dive deeper?
We had last left off saying that answer for a certain n is [X^n] \prod_{i} \frac{1-X^{(b_i+1)a_i}}{1-X^{a_i}}.
Let’s take the natural log, and see what happens:
- F(X) = \prod_{i} \frac{1-X^{(b_i+1)a_i}}{1-X^{a_i}}
- \ln(F(X)) = \sum_{i}\ln( \frac{1-X^{(b_i+1)a_i}}{1-X^{a_i}})
- \ln(F(X)) = \sum_{i} \ln(1-X^{(b_i+1)a_i}) -\sum_{i} \ln(1-X^{a_i})
Now we use the aforementioned expansion of natural log, and since for a particular a_i, there can be only \frac{n}{a_i} non-zero terms in the expansion of \ln (1-X^{a_i}) (Look Closely at equation (1))(Note that we only care for exponents at most N), thus, we can group all the different exponents togther, and find \ln(F(X)) in Nlog N time (Remember that \frac{N}{1} + \frac{N}{2} + \frac{N}{3} + ... \frac{N}{N} = O(NlogN)). From here, we can also find F(X) in O(NlogN) time using polynomial exponentiation. Hence, we are done! See Setter’s code for how to implement it.
MORE RESOURCES:
More on Generating Functions.
Library for Polynomial methods
Power series for \ln (1-X)
Operations on Polynomials
SOLUTIONS:
Setter's Code
#include <bits/stdc++.h>
using namespace std;
const int md = 998244353;
namespace faq{
inline void add(int &x, int y) {
x += y;
if (x >= md) {
x -= md;
}
}
inline void sub(int &x, int y) {
x -= y;
if (x < 0) {
x += md;
}
}
inline int mul(int x, int y) {
return (long long) x * y % md;
}
inline int power(int x, int y) {
int res = 1;
for (; y; y >>= 1, x = mul(x, x)) {
if (y & 1) {
res = mul(res, x);
}
}
return res;
}
inline int inv(int a) {
a %= md;
if (a < 0) {
a += md;
}
int b = md, u = 0, v = 1;
while (a) {
int t = b / a;
b -= t * a;
swap(a, b);
u -= t * v;
swap(u, v);
}
if (u < 0) {
u += md;
}
return u;
}
namespace ntt {
int base = 1, root = -1, max_base = -1;
vector<int> rev = {0, 1}, roots = {0, 1};
void init() {
int temp = md - 1;
max_base = 0;
while (temp % 2 == 0) {
temp >>= 1;
++max_base;
}
root = 2;
while (true) {
if (power(root, 1 << max_base) == 1 && power(root, 1 << max_base - 1) != 1) {
break;
}
++root;
}
}
void ensure_base(int nbase) {
if (max_base == -1) {
init();
}
if (nbase <= base) {
return;
}
assert(nbase <= max_base);
rev.resize(1 << nbase);
for (int i = 0; i < 1 << nbase; ++i) {
rev[i] = rev[i >> 1] >> 1 | (i & 1) << nbase - 1;
}
roots.resize(1 << nbase);
while (base < nbase) {
int z = power(root, 1 << max_base - 1 - base);
for (int i = 1 << base - 1; i < 1 << base; ++i) {
roots[i << 1] = roots[i];
roots[i << 1 | 1] = mul(roots[i], z);
}
++base;
}
}
void dft(vector<int> &a) {
int n = a.size(), zeros = __builtin_ctz(n);
ensure_base(zeros);
int shift = base - zeros;
for (int i = 0; i < n; ++i) {
if (i < rev[i] >> shift) {
swap(a[i], a[rev[i] >> shift]);
}
}
for (int i = 1; i < n; i <<= 1) {
for (int j = 0; j < n; j += i << 1) {
for (int k = 0; k < i; ++k) {
int x = a[j + k], y = mul(a[j + k + i], roots[i + k]);
a[j + k] = (x + y) % md;
a[j + k + i] = (x + md - y) % md;
}
}
}
}
vector<int> multiply(vector<int> a, vector<int> b) {
int need = a.size() + b.size() - 1, nbase = 0;
while (1 << nbase < need) {
++nbase;
}
ensure_base(nbase);
int sz = 1 << nbase;
a.resize(sz);
b.resize(sz);
bool equal = a == b;
dft(a);
if (equal) {
b = a;
} else {
dft(b);
}
int inv_sz = inv(sz);
for (int i = 0; i < sz; ++i) {
a[i] = mul(mul(a[i], b[i]), inv_sz);
}
reverse(a.begin() + 1, a.end());
dft(a);
a.resize(need);
return a;
}
vector<int> inverse(vector<int> a) {
int n = a.size(), m = n + 1 >> 1;
if (n == 1) {
return vector<int>(1, inv(a[0]));
} else {
vector<int> b = inverse(vector<int>(a.begin(), a.begin() + m));
int need = n << 1, nbase = 0;
while (1 << nbase < need) {
++nbase;
}
ensure_base(nbase);
int sz = 1 << nbase;
a.resize(sz);
b.resize(sz);
dft(a);
dft(b);
int inv_sz = inv(sz);
for (int i = 0; i < sz; ++i) {
a[i] = mul(mul(md + 2 - mul(a[i], b[i]), b[i]), inv_sz);
}
reverse(a.begin() + 1, a.end());
dft(a);
a.resize(n);
return a;
}
}
}
using ntt::multiply;
using ntt::inverse;
vector<int>& operator += (vector<int> &a, const vector<int> &b) {
if (a.size() < b.size()) {
a.resize(b.size());
}
for (int i = 0; i < b.size(); ++i) {
add(a[i], b[i]);
}
return a;
}
vector<int> operator + (const vector<int> &a, const vector<int> &b) {
vector<int> c = a;
return c += b;
}
vector<int>& operator -= (vector<int> &a, const vector<int> &b) {
if (a.size() < b.size()) {
a.resize(b.size());
}
for (int i = 0; i < b.size(); ++i) {
sub(a[i], b[i]);
}
return a;
}
vector<int> operator - (const vector<int> &a, const vector<int> &b) {
vector<int> c = a;
return c -= b;
}
vector<int>& operator *= (vector<int> &a, const vector<int> &b) {
if (min(a.size(), b.size()) < 128) {
vector<int> c = a;
a.assign(a.size() + b.size() - 1, 0);
for (int i = 0; i < c.size(); ++i) {
for (int j = 0; j < b.size(); ++j) {
add(a[i + j], mul(c[i], b[j]));
}
}
} else {
a = multiply(a, b);
}
return a;
}
vector<int> operator * (const vector<int> &a, const vector<int> &b) {
vector<int> c = a;
return c *= b;
}
vector<int>& operator /= (vector<int> &a, const vector<int> &b) {
int n = a.size(), m = b.size();
if (n < m) {
a.clear();
} else {
vector<int> c = b;
reverse(a.begin(), a.end());
reverse(c.begin(), c.end());
c.resize(n - m + 1);
a *= inverse(c);
a.erase(a.begin() + n - m + 1, a.end());
reverse(a.begin(), a.end());
}
return a;
}
vector<int> operator / (const vector<int> &a, const vector<int> &b) {
vector<int> c = a;
return c /= b;
}
vector<int>& operator %= (vector<int> &a, const vector<int> &b) {
int n = a.size(), m = b.size();
if (n >= m) {
vector<int> c = (a / b) * b;
a.resize(m - 1);
for (int i = 0; i < m - 1; ++i) {
sub(a[i], c[i]);
}
}
return a;
}
vector<int> operator % (const vector<int> &a, const vector<int> &b) {
vector<int> c = a;
return c %= b;
}
vector<int> derivative(const vector<int> &a) {
int n = a.size();
vector<int> b(n - 1);
for (int i = 1; i < n; ++i) {
b[i - 1] = mul(a[i], i);
}
return b;
}
vector<int> primitive(const vector<int> &a) {
int n = a.size();
vector<int> b(n + 1), invs(n + 1);
for (int i = 1; i <= n; ++i) {
invs[i] = i == 1 ? 1 : mul(md - md / i, invs[md % i]);
b[i] = mul(a[i - 1], invs[i]);
}
return b;
}
vector<int> logarithm(const vector<int> &a) {
vector<int> b = primitive(derivative(a) * inverse(a));
b.resize(a.size());
return b;
}
vector<int> exponent(const vector<int> &a) {
vector<int> b(1, 1);
while (b.size() < a.size()) {
vector<int> c(a.begin(), a.begin() + min(a.size(), b.size() << 1));
add(c[0], 1);
vector<int> old_b = b;
b.resize(b.size() << 1);
c -= logarithm(b);
c *= old_b;
for (int i = b.size() >> 1; i < b.size(); ++i) {
b[i] = c[i];
}
}
b.resize(a.size());
return b;
}
vector<int> power(const vector<int> &a, int m) {
int n = a.size(), p = -1;
vector<int> b(n);
for (int i = 0; i < n; ++i) {
if (a[i]) {
p = i;
break;
}
}
if (p == -1) {
b[0] = !m;
return b;
}
if ((long long) m * p >= n) {
return b;
}
int mu = power(a[p], m), di = inv(a[p]);
vector<int> c(n - m * p);
for (int i = 0; i < n - m * p; ++i) {
c[i] = mul(a[i + p], di);
}
c = logarithm(c);
for (int i = 0; i < n - m * p; ++i) {
c[i] = mul(c[i], m);
}
c = exponent(c);
for (int i = 0; i < n - m * p; ++i) {
b[i + m * p] = mul(c[i], mu);
}
return b;
}
vector<int> sqrt(const vector<int> &a) {
vector<int> b(1, 1);
while (b.size() < a.size()) {
vector<int> c(a.begin(), a.begin() + min(a.size(), b.size() << 1));
vector<int> old_b = b;
b.resize(b.size() << 1);
c *= inverse(b);
for (int i = b.size() >> 1; i < b.size(); ++i) {
b[i] = mul(c[i], md + 1 >> 1);
}
}
b.resize(a.size());
return b;
}
vector<int> multiply_all(int l, int r, vector<vector<int>> &all) {
if (l > r) {
return vector<int>();
} else if (l == r) {
return all[l];
} else {
int y = l + r >> 1;
return multiply_all(l, y, all) * multiply_all(y + 1, r, all);
}
}
vector<int> evaluate(const vector<int> &f, const vector<int> &x) {
int n = x.size();
if (!n) {
return vector<int>();
}
vector<vector<int>> up(n * 2);
for (int i = 0; i < n; ++i) {
up[i + n] = vector<int>{(md - x[i]) % md, 1};
}
for (int i = n - 1; i; --i) {
up[i] = up[i << 1] * up[i << 1 | 1];
}
vector<vector<int>> down(n * 2);
down[1] = f % up[1];
for (int i = 2; i < n * 2; ++i) {
down[i] = down[i >> 1] % up[i];
}
vector<int> y(n);
for (int i = 0; i < n; ++i) {
y[i] = down[i + n][0];
}
return y;
}
vector<int> interpolate(const vector<int> &x, const vector<int> &y) {
int n = x.size();
vector<vector<int>> up(n * 2);
for (int i = 0; i < n; ++i) {
up[i + n] = vector<int>{(md - x[i]) % md, 1};
}
for (int i = n - 1; i; --i) {
up[i] = up[i << 1] * up[i << 1 | 1];
}
vector<int> a = evaluate(derivative(up[1]), x);
for (int i = 0; i < n; ++i) {
a[i] = mul(y[i], inv(a[i]));
}
vector<vector<int>> down(n * 2);
for (int i = 0; i < n; ++i) {
down[i + n] = vector<int>(1, a[i]);
}
for (int i = n - 1; i; --i) {
down[i] = down[i << 1] * up[i << 1 | 1] + down[i << 1 | 1] * up[i << 1];
}
return down[1];
}
}
typedef long long ll;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, q;
cin >> n >> q;
vector <int> val(n + 1), f(n + 1), coef(n + 1);
for (int i = 0; i < q; i++) {
int a, b;
cin >> a >> b;
coef[a]++;
if (a * (ll) (b + 1) <= n) {
coef[a * (ll) (b + 1)]--;
}
}
for (int i = 1; i <= n; i++) {
if (coef[i] < 0) coef[i] += md;
}
for (int i = 1; i <= n; i++) {
val[i] = faq::inv(i);
}
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j += i) {
faq::add(f[j], faq::mul(val[j / i], coef[i]));
}
}
f = faq::exponent(f);
for (int i = 1; i <= n; i++) cout << f[i] << ' ';
cout << endl;
}
Tester's Code
#include <bits/stdc++.h>
using namespace std;
/**
Reference:
https://cp-algorithms.com/algebra/polynomial.html
https://github.com/e-maxx-eng/e-maxx-eng-aux/blob/master/src/polynomial.cpp
**/
namespace algebra {
const int inf = 1e9;
const int magic = 500; // threshold for sizes to run the naive algo
namespace fft {
const int maxn = 1 << 19;
typedef double ftype;
typedef complex<ftype> point;
point w[maxn];
const ftype pi = acos(-1);
bool initiated = 0;
void init() {
if(!initiated) {
for(int i = 1; i < maxn; i *= 2) {
for(int j = 0; j < i; j++) {
w[i + j] = polar(ftype(1), pi * j / i);
}
}
initiated = 1;
}
}
template<typename T>
void fft(T *in, point *out, int n, int k = 1) {
if(n == 1) {
*out = *in;
} else {
n /= 2;
fft(in, out, n, 2 * k);
fft(in + k, out + n, n, 2 * k);
for(int i = 0; i < n; i++) {
auto t = out[i + n] * w[i + n];
out[i + n] = out[i] - t;
out[i] += t;
}
}
}
template<typename T>
void mul_slow(vector<T> &a, const vector<T> &b) {
vector<T> res(a.size() + b.size() - 1);
for(size_t i = 0; i < a.size(); i++) {
for(size_t j = 0; j < b.size(); j++) {
res[i + j] += a[i] * b[j];
}
}
a = res;
}
template<typename T>
void mul(vector<T> &a, const vector<T> &b) {
if(min(a.size(), b.size()) < magic) {
mul_slow(a, b);
return;
}
init();
static const int shift = 15, mask = (1 << shift) - 1;
size_t n = a.size() + b.size() - 1;
while(__builtin_popcount(n) != 1) {
n++;
}
a.resize(n);
static point A[maxn], B[maxn];
static point C[maxn], D[maxn];
for(size_t i = 0; i < n; i++) {
A[i] = point(a[i] & mask, a[i] >> shift);
if(i < b.size()) {
B[i] = point(b[i] & mask, b[i] >> shift);
} else {
B[i] = 0;
}
}
fft(A, C, n); fft(B, D, n);
for(size_t i = 0; i < n; i++) {
point c0 = C[i] + conj(C[(n - i) % n]);
point c1 = C[i] - conj(C[(n - i) % n]);
point d0 = D[i] + conj(D[(n - i) % n]);
point d1 = D[i] - conj(D[(n - i) % n]);
A[i] = c0 * d0 - point(0, 1) * c1 * d1;
B[i] = c0 * d1 + d0 * c1;
}
fft(A, C, n); fft(B, D, n);
reverse(C + 1, C + n);
reverse(D + 1, D + n);
int t = 4 * n;
for(size_t i = 0; i < n; i++) {
int64_t A0 = llround(real(C[i]) / t);
T A1 = llround(imag(D[i]) / t);
T A2 = llround(imag(C[i]) / t);
a[i] = A0 + (A1 << shift) + (A2 << 2 * shift);
}
return;
}
}
template<typename T>
T bpow(T x, size_t n) {
return n ? n % 2 ? x * bpow(x, n - 1) : bpow(x * x, n / 2) : T(1);
}
template<typename T>
T bpow(T x, size_t n, T m) {
return n ? n % 2 ? x * bpow(x, n - 1, m) % m : bpow(x * x % m, n / 2, m) : T(1);
}
template<typename T>
T gcd(const T &a, const T &b) {
return b == T(0) ? a : gcd(b, a % b);
}
template<typename T>
T nCr(T n, int r) { // runs in O(r)
T res(1);
for(int i = 0; i < r; i++) {
res *= (n - T(i));
res /= (i + 1);
}
return res;
}
template<int m>
struct modular {
int64_t r;
modular() : r(0) {}
modular(int64_t rr) : r(rr) {if(abs(r) >= m) r %= m; if(r < 0) r += m;}
modular inv() const {return bpow(*this, m - 2);}
modular operator * (const modular &t) const {return (r * t.r) % m;}
modular operator / (const modular &t) const {return *this * t.inv();}
modular operator += (const modular &t) {r += t.r; if(r >= m) r -= m; return *this;}
modular operator -= (const modular &t) {r -= t.r; if(r < 0) r += m; return *this;}
modular operator + (const modular &t) const {return modular(*this) += t;}
modular operator - (const modular &t) const {return modular(*this) -= t;}
modular operator *= (const modular &t) {return *this = *this * t;}
modular operator /= (const modular &t) {return *this = *this / t;}
bool operator == (const modular &t) const {return r == t.r;}
bool operator != (const modular &t) const {return r != t.r;}
operator int64_t() const {return r;}
};
template<int T>
istream& operator >> (istream &in, modular<T> &x) {
return in >> x.r;
}
template<typename T>
struct poly {
vector<T> a;
void normalize() { // get rid of leading zeroes
while(!a.empty() && a.back() == T(0)) {
a.pop_back();
}
}
poly(){}
poly(T a0) : a{a0}{normalize();}
poly(vector<T> t) : a(t){normalize();}
poly operator += (const poly &t) {
a.resize(max(a.size(), t.a.size()));
for(size_t i = 0; i < t.a.size(); i++) {
a[i] += t.a[i];
}
normalize();
return *this;
}
poly operator -= (const poly &t) {
a.resize(max(a.size(), t.a.size()));
for(size_t i = 0; i < t.a.size(); i++) {
a[i] -= t.a[i];
}
normalize();
return *this;
}
poly operator + (const poly &t) const {return poly(*this) += t;}
poly operator - (const poly &t) const {return poly(*this) -= t;}
poly mod_xk(size_t k) const { // get same polynomial mod x^k
k = min(k, a.size());
return vector<T>(begin(a), begin(a) + k);
}
poly mul_xk(size_t k) const { // multiply by x^k
poly res(*this);
res.a.insert(begin(res.a), k, 0);
return res;
}
poly div_xk(size_t k) const { // divide by x^k, dropping coefficients
k = min(k, a.size());
return vector<T>(begin(a) + k, end(a));
}
poly substr(size_t l, size_t r) const { // return mod_xk(r).div_xk(l)
l = min(l, a.size());
r = min(r, a.size());
return vector<T>(begin(a) + l, begin(a) + r);
}
poly inv(size_t n) const { // get inverse series mod x^n
assert(!is_zero());
poly ans = a[0].inv();
size_t a = 1;
while(a < n) {
poly C = (ans * mod_xk(2 * a)).substr(a, 2 * a);
ans -= (ans * C).mod_xk(a).mul_xk(a);
a *= 2;
}
return ans.mod_xk(n);
}
poly operator *= (const poly &t) {fft::mul(a, t.a); normalize(); return *this;}
poly operator * (const poly &t) const {return poly(*this) *= t;}
poly reverse(size_t n, bool rev = 0) const { // reverses and leaves only n terms
poly res(*this);
if(rev) { // If rev = 1 then tail goes to head
res.a.resize(max(n, res.a.size()));
}
std::reverse(res.a.begin(), res.a.end());
return res.mod_xk(n);
}
pair<poly, poly> divmod_slow(const poly &b) const { // when divisor or quotient is small
vector<T> A(a);
vector<T> res;
while(A.size() >= b.a.size()) {
res.push_back(A.back() / b.a.back());
if(res.back() != T(0)) {
for(size_t i = 0; i < b.a.size(); i++) {
A[A.size() - i - 1] -= res.back() * b.a[b.a.size() - i - 1];
}
}
A.pop_back();
}
std::reverse(begin(res), end(res));
return {res, A};
}
pair<poly, poly> divmod(const poly &b) const { // returns quotiend and remainder of a mod b
if(deg() < b.deg()) {
return {poly{0}, *this};
}
int d = deg() - b.deg();
if(min(d, b.deg()) < magic) {
return divmod_slow(b);
}
poly D = (reverse(d + 1) * b.reverse(d + 1).inv(d + 1)).mod_xk(d + 1).reverse(d + 1, 1);
return {D, *this - D * b};
}
poly operator / (const poly &t) const {return divmod(t).first;}
poly operator % (const poly &t) const {return divmod(t).second;}
poly operator /= (const poly &t) {return *this = divmod(t).first;}
poly operator %= (const poly &t) {return *this = divmod(t).second;}
poly operator *= (const T &x) {
for(auto &it: a) {
it *= x;
}
normalize();
return *this;
}
poly operator /= (const T &x) {
for(auto &it: a) {
it /= x;
}
normalize();
return *this;
}
poly operator * (const T &x) const {return poly(*this) *= x;}
poly operator / (const T &x) const {return poly(*this) /= x;}
void print() const {
for(auto it: a) {
cout << it << ' ';
}
cout << endl;
}
T eval(T x) const { // evaluates in single point x
T res(0);
for(int i = int(a.size()) - 1; i >= 0; i--) {
res *= x;
res += a[i];
}
return res;
}
T& lead() { // leading coefficient
return a.back();
}
int deg() const { // degree
return a.empty() ? -inf : a.size() - 1;
}
bool is_zero() const { // is polynomial zero
return a.empty();
}
T operator [](int idx) const {
return idx >= (int)a.size() || idx < 0 ? T(0) : a[idx];
}
T& coef(size_t idx) { // mutable reference at coefficient
return a[idx];
}
bool operator == (const poly &t) const {return a == t.a;}
bool operator != (const poly &t) const {return a != t.a;}
poly deriv() { // calculate derivative
vector<T> res;
for(int i = 1; i <= deg(); i++) {
res.push_back(T(i) * a[i]);
}
return res;
}
poly integr() { // calculate integral with C = 0
vector<T> res = {0};
for(int i = 0; i <= deg(); i++) {
res.push_back(a[i] / T(i + 1));
}
return res;
}
size_t leading_xk() const { // Let p(x) = x^k * t(x), return k
if(is_zero()) {
return inf;
}
int res = 0;
while(a[res] == T(0)) {
res++;
}
return res;
}
poly log(size_t n) { // calculate log p(x) mod x^n
assert(a[0] == T(1));
return (deriv().mod_xk(n) * inv(n)).integr().mod_xk(n);
}
poly exp(size_t n) { // calculate exp p(x) mod x^n
if(is_zero()) {
return T(1);
}
assert(a[0] == T(0));
poly ans = T(1);
size_t a = 1;
while(a < n) {
poly C = ans.log(2 * a).div_xk(a) - substr(a, 2 * a);
ans -= (ans * C).mod_xk(a).mul_xk(a);
a *= 2;
}
return ans.mod_xk(n);
}
poly pow_slow(size_t k, size_t n) { // if k is small
return k ? k % 2 ? (*this * pow_slow(k - 1, n)).mod_xk(n) : (*this * *this).mod_xk(n).pow_slow(k / 2, n) : T(1);
}
poly pow(size_t k, size_t n) { // calculate p^k(n) mod x^n
if(is_zero()) {
return *this;
}
if(k < magic) {
return pow_slow(k, n);
}
int i = leading_xk();
T j = a[i];
poly t = div_xk(i) / j;
return bpow(j, k) * (t.log(n) * T(k)).exp(n).mul_xk(i * k).mod_xk(n);
}
poly mulx(T x) { // component-wise multiplication with x^k
T cur = 1;
poly res(*this);
for(int i = 0; i <= deg(); i++) {
res.coef(i) *= cur;
cur *= x;
}
return res;
}
poly mulx_sq(T x) { // component-wise multiplication with x^{k^2}
T cur = x;
T total = 1;
T xx = x * x;
poly res(*this);
for(int i = 0; i <= deg(); i++) {
res.coef(i) *= total;
total *= cur;
cur *= xx;
}
return res;
}
vector<T> chirpz_even(T z, int n) { // P(1), P(z^2), P(z^4), ..., P(z^2(n-1))
int m = deg();
if(is_zero()) {
return vector<T>(n, 0);
}
vector<T> vv(m + n);
T zi = z.inv();
T zz = zi * zi;
T cur = zi;
T total = 1;
for(int i = 0; i <= max(n - 1, m); i++) {
if(i <= m) {vv[m - i] = total;}
if(i < n) {vv[m + i] = total;}
total *= cur;
cur *= zz;
}
poly w = (mulx_sq(z) * vv).substr(m, m + n).mulx_sq(z);
vector<T> res(n);
for(int i = 0; i < n; i++) {
res[i] = w[i];
}
return res;
}
vector<T> chirpz(T z, int n) { // P(1), P(z), P(z^2), ..., P(z^(n-1))
auto even = chirpz_even(z, (n + 1) / 2);
auto odd = mulx(z).chirpz_even(z, n / 2);
vector<T> ans(n);
for(int i = 0; i < n / 2; i++) {
ans[2 * i] = even[i];
ans[2 * i + 1] = odd[i];
}
if(n % 2 == 1) {
ans[n - 1] = even.back();
}
return ans;
}
template<typename iter>
vector<T> eval(vector<poly> &tree, int v, iter l, iter r) { // auxiliary evaluation function
if(r - l == 1) {
return {eval(*l)};
} else {
auto m = l + (r - l) / 2;
auto A = (*this % tree[2 * v]).eval(tree, 2 * v, l, m);
auto B = (*this % tree[2 * v + 1]).eval(tree, 2 * v + 1, m, r);
A.insert(end(A), begin(B), end(B));
return A;
}
}
vector<T> eval(vector<T> x) { // evaluate polynomial in (x1, ..., xn)
int n = x.size();
if(is_zero()) {
return vector<T>(n, T(0));
}
vector<poly> tree(4 * n);
build(tree, 1, begin(x), end(x));
return eval(tree, 1, begin(x), end(x));
}
template<typename iter>
poly inter(vector<poly> &tree, int v, iter l, iter r, iter ly, iter ry) { // auxiliary interpolation function
if(r - l == 1) {
return {*ly / a[0]};
} else {
auto m = l + (r - l) / 2;
auto my = ly + (ry - ly) / 2;
auto A = (*this % tree[2 * v]).inter(tree, 2 * v, l, m, ly, my);
auto B = (*this % tree[2 * v + 1]).inter(tree, 2 * v + 1, m, r, my, ry);
return A * tree[2 * v + 1] + B * tree[2 * v];
}
}
};
template<typename T>
poly<T> operator * (const T& a, const poly<T>& b) {
return b * a;
}
template<typename T>
poly<T> xk(int k) { // return x^k
return poly<T>{1}.mul_xk(k);
}
template<typename T>
T resultant(poly<T> a, poly<T> b) { // computes resultant of a and b
if(b.is_zero()) {
return 0;
} else if(b.deg() == 0) {
return bpow(b.lead(), a.deg());
} else {
int pw = a.deg();
a %= b;
pw -= a.deg();
T mul = bpow(b.lead(), pw) * T((b.deg() & a.deg() & 1) ? -1 : 1);
T ans = resultant(b, a);
return ans * mul;
}
}
template<typename iter>
poly<typename iter::value_type> kmul(iter L, iter R) { // computes (x-a1)(x-a2)...(x-an) without building tree
if(R - L == 1) {
return vector<typename iter::value_type>{-*L, 1};
} else {
iter M = L + (R - L) / 2;
return kmul(L, M) * kmul(M, R);
}
}
template<typename T, typename iter>
poly<T> build(vector<poly<T>> &res, int v, iter L, iter R) { // builds evaluation tree for (x-a1)(x-a2)...(x-an)
if(R - L == 1) {
return res[v] = vector<T>{-*L, 1};
} else {
iter M = L + (R - L) / 2;
return res[v] = build(res, 2 * v, L, M) * build(res, 2 * v + 1, M, R);
}
}
template<typename T>
poly<T> inter(vector<T> x, vector<T> y) { // interpolates minimum polynomial from (xi, yi) pairs
int n = x.size();
vector<poly<T>> tree(4 * n);
return build(tree, 1, begin(x), end(x)).deriv().inter(tree, 1, begin(x), end(x), begin(y), end(y));
}
};
using namespace algebra;
const int mod = 998244353;
typedef modular<mod> base;
typedef poly<base> polyn;
/**
Solution outline:
\prod_{1}^{Q} \frac{1 - x^{(ai * (bi + 1))}}{1 - ai*x} =
\exp(\log (\prod_{1}^{Q} \frac{1 - x^{(ai * (bi + 1))}}{1 - ai*x})) =
\exp(\sum_{1}^{Q} \log(\frac{1 - x^{(ai * (bi + 1))}}{1 - ai*x})) =
\exp(\sum_{1}^{Q} \log({1 - x^{(ai * (bi + 1))}}) - log(1 - ai*x))
MUL_{1..Q} (1 - x ^ (a * (b + 1))) / (1 - x ^ a) =
exp(log (MUL_{1..Q} (1 - x ^ (ai * (bi + 1))) / (1 - x ^ ai))) =
exp(ADD_{1..Q} log((1 - x ^ (ai * (bi + 1))) / (1 - x ^ ai)))) =
exp(ADD_{1..Q} log(1 - x ^ (ai * (bi + 1))) - log(1 - x ^ ai))
**/
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, q;
cin >> n >> q;
vector<base> cnt_power(n + 1, 0), lg_sum(n + 1, 0);
for(int i = 0; i < q; i++){
int a, b;
cin >> a >> b;
cnt_power[a] += 1;
if(1ll * a * (b + 1) <= n)
cnt_power[a * (b + 1)] -= 1;
}
for(int i = 1; i <= n; i++){
base inv = base(1) / base(i);
for(int j = 1; j * i <= n; j++){
lg_sum[j * i] += cnt_power[j] * inv;
}
}
polyn poly(lg_sum);
poly = poly.exp(n + 1);
for(int i = 1; i <= n; i++){
if(i > 1){
cout << ' ';
}
cout << poly.a[i];
}
cout << '\n';
return 0;
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()