PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Sumegh Roychowdhury
Tester: Zhong Ziqian
Editorialist: Taranpreet Singh
DIFFICULTY:
Simple
PREREQUISITES:
Basic Math would be enough. Greatest Common Divisor and Simulation.
PROBLEM:
Find the position of Kth Ridge on a cardboard when the following procedure is performed Kth time, alternatively
Pick the right side of the board and fold it so that it matches with the left end. OR
Pick up the left end of the board and fold it to meet the right end of cardboard.
SUPER QUICK EXPLANATION
- The new ridge formed is always the midpoint between the previous two ridges formed. For a start, We can see, that the first two ridges are at positions 1/2 and 1/4 respectively.
EXPLANATION
Let us first understand how ridges are being created.
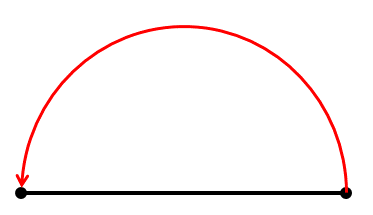
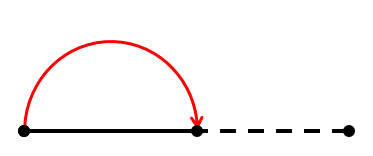
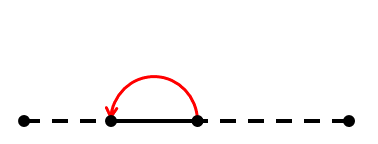
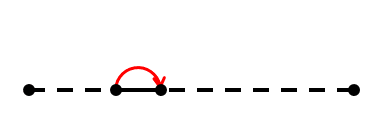
We can see, that the size of cardboard gets reduced to half, and the ridge is formed at left or right end of cardboard alternatingly.
So, it is not hard to see, that at every step,
It is not hard to see, that every time we fold the cardboard, we form a new ridge, which is exactly at the midpoint of the previous two ridges.
This gives way to the solution. At every step, we can find the midpoint of the previous two ridges and use it for calculating the positions of next ridges. Since N is quite Small, we can even precompute answers for all values of N.
Now, We need to print the answer in reduced form. Basically, if two number A and B have GCD G, then (A/G)/(B/G) represent the same fraction in reduced terms.
GCD of two numbers can be easily found using Euclid’s GCD algorithm, which you may find here.
As for first two ridges, we can assume Right end and the Left end to be first and second ridge respectively, for a simpler implementation, or just see positions of first two ridges from samples.
Time Complexity
Time complexity is O(N) per test case.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()