Need explanation in problem many squares CodeChef: Practical coding for everyone
Editorials will be out soon.
Okk
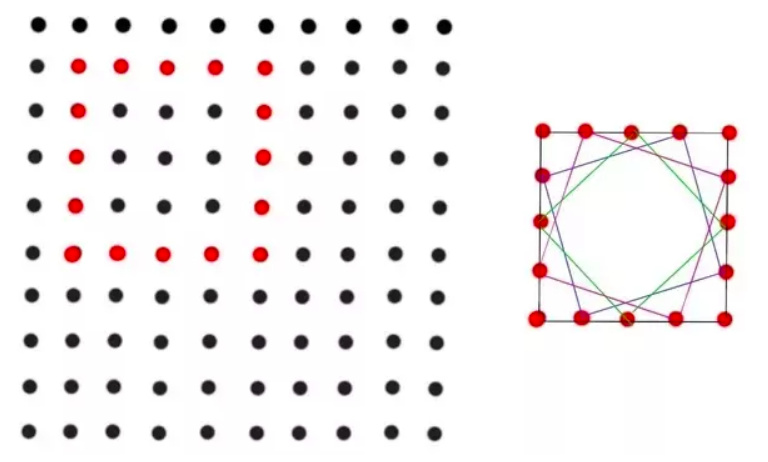
We have to find the sum of areas of all possible squares formed in a m* n grid of points. A square is valid if all its vertices lie on the points of m* n grid
That I also know but I want the explainaton to second test case
4 7
502
For a square of size k, there exist k-1 more squares embedded in it(of different sizes).
ex: for k=3, there is an outer square of side 3, and 2 squares of side sqrt(5) and so on…
Let m \leq n without loss of generality
Sum of Areas of all squares in m \times n grid be A(m, n)
A(m, n) = \sum_{i = 1}^m(m-i+1) \times(n - i + 1) \times S(i)
S(k) is the sum of areas of squares in k \times k grid with vertices on the perimeter
It can be observed that
S(k) = \sum_{i = 0}^{k-1} (i^2 + (k-i)^2)
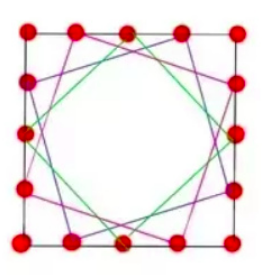
I used the same approach, this is giving TLE in my case.
After expanding it, let k_1 = (m+1)(n+1) , k_2 = (m + n + 2)
A(m, n) = \sum_{i = 1}^{m}(2i^5 - 2k_2i^4 + (2k_1+1)i^3 - k_2i^2+k_1i)/3
Use sum of k th powers of first n natural number’s formulae to answer each test case in O(1)
My submission: Link
Thanks a lot!
thanks brother
soon ?