PROBLEM LINK:
Author: admin3
Testers: Hasan Jaddouh
Editorialist: Pawel Kacprzak
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Greedy, sortings, segments geometry
PROBLEM:
Given a grid of with N rows and N columns, with special square grid of size K \times K in its center, and position of M snakes (vertical of horizontal segments of consecutive cells), where no snakes are inside the special square, the task is to leave minimum number of snakes on the grid (remove the maximum unnecessary snakes), so that the special square will be protected by the remaining snakes. The special square is protected by the snakes if and only if there doesn’t exist an arrow that can be shot along a row or a column, which can enter the special square and leave the whole grid on the other side. Notice that arrows can pass only cells not occupied by snakes.
EXPLANATION:
We say that a snake protects a side of the special square if and only if there exists an arrow that can be shot as described in the statement and the snake prevents it either from entering the special square or leaving it on the other side. The first thing to notice is that there is no snake which can protect both a vertical and horizontal side of the special grid at the same time. This is true because snakes are straight segments. Thus the problem can be divided into two separate problems: finding the minimum number of snakes required to protect horizontal sides of the special square and finding the minimum number of snakes required to protect vertical sides of the special square. We’ll focus here on the first of these problems because the solution to the other one follows the same idea.
Now, we want to find the minimum number of snakes required to protect horizontal sides of the special square. Let’s reformulate the problem a little bit. Snakes denote horizontal segments, and the set of all these segments is S. We have also a special horizontal segment A which we want to cover completely by the minimum, in terms of the number of elements, subset of S. Notice that A is the segment denoting the top (or the bottom, it doesn’t matter, because we only care about horizontal coordinates) side of the special square, and that set S can be computed as the set of the snakes with a non-empty intersection with A on the horizontal axis. For example, as illustrated in the below picture, the set S contains red, blue and orange snakes:
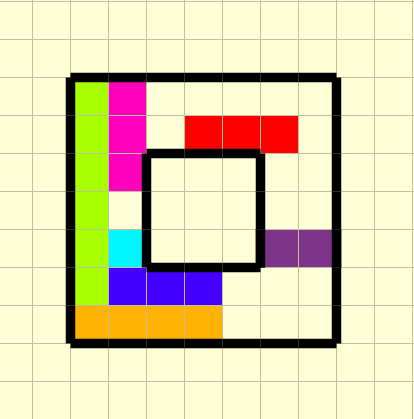
We reduced the original problem to a problem of finding the smallest subset of the given set of horizontal segments S, which covers completely the whole segment A. This is one of the classical problems, which can be solved greedily. The idea is to sort the segments in S by their left endpoints and process them from left to right in that order trying to cover the left-most not yet covered point of A. More specifically, let’s assume that x is the left-most not yet covered point of A. We examine all segments from S with left endpoint not greater than x and we take to the result the one with the largest right endpoint. Let this largest endpoint be k, so we update x to k+1 and continue the process until either all points of A are covered, so we have the result, or we examined all segments, which means that there is no way to cover A.
The total complexity of this solution is O(N \cdot \log(N)) and it’s dominated by sorting time. Notice that we need to solve this problem two times: one for horizontal sides of the special square, and second, for the vertical sides of the special square. If at least one of these problems has no solution, we, of course, return -1 as the final answer.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution can be found here.
Tester’s solution can be found here.
Editorialist’s solution can be found here.
