PROBLEM LINK:
Author: Pavel Sheftelevich
Tester: Vlad Mosko
Editorialist: Pawel Kacprzak
DIFFICULTY:
MEDIUM
PREREQUISITES:
PROBLEM:
You are given an N \times N grid and K special distinct cells in it. For each of these K cells, let’s say (i, j), we know that all cells which lie on the same diagonals as (i, j) are full of cats.
For example, here are a few diagonals marked on 5 \times 5 grid:
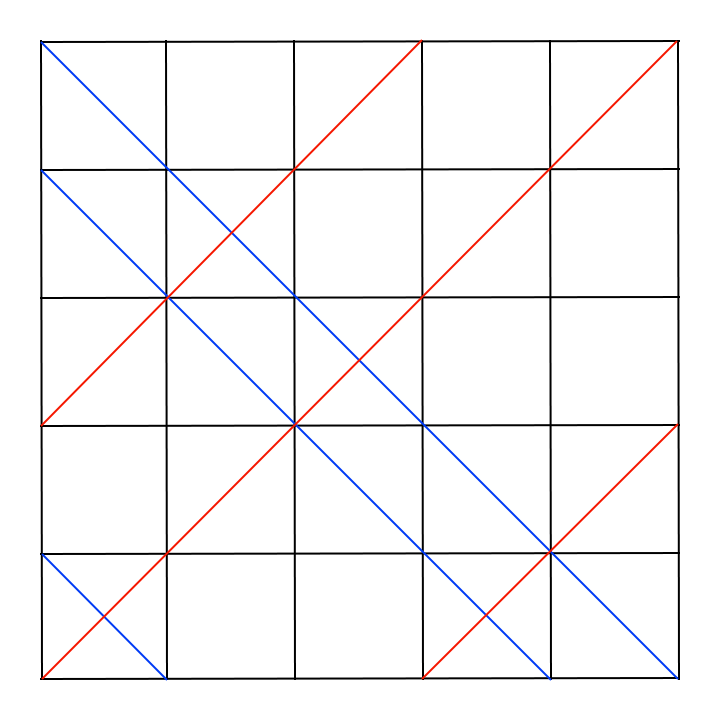
We call blue diagonals left diagonals and red diagonals right ones.
The task is to find out how many cells on the grid are free of cats.
The most straightforward solution is to for each of the given K cells, let’s say (i, j), mark all cells which lie on the same diagonals as (i, j). Since there is always one left and one right diagonal crossing any cell, we have to mark at most O(N) cells for each input cell. At the end we need to subtract the number of marked cells from all cells in the grid. This solution requires total O(N^3) time and might pass some small testcases, but we have to do better.
Let’s enumerate our diagonals first.
Let’s consider any cell (i, j), where i is the row number and j is the column number.
For each left diagonal (a blue one), all cells lying on this diagonal has the same value of i - j. In order to enumerate left diagonals, let’s assign to each one a single integer i - j + N. This allows us to refer to left diagonals by numbers 1, 2, \ldots, 2 \cdot N - 1.
We can make a similar mapping for right diagonals (red ones). Notice that all cells lying on one right diagonal has the same value of i + j. In order to enumerate right diagonals, let’s assign a single integer i + j - 1 to each one. This allows us to refer to right diagonals by numbers 1, 2, \ldots, 2 \cdot N - 1.
This two enumerations are explained further on below drawings:
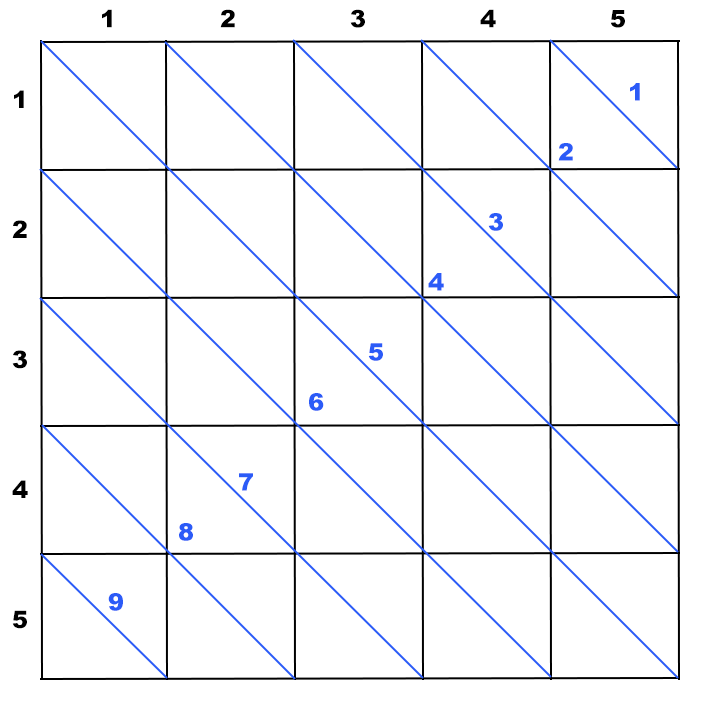
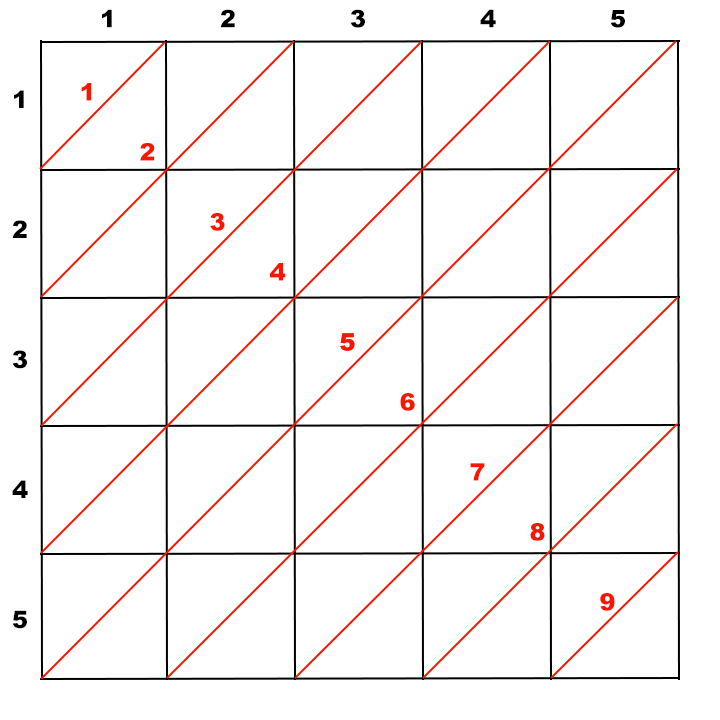
Being able to enumerate the diagonals, while iterating over input cells, we can mark diagonals as occupied by cats. In order to do that, for each input cell, compute the index of left and right diagonals which crosses it and mark them as occupied by cats.
To get the result, we can iterate over all grid cells and for each one, we check if any diagonal crossing it is occupied by cats. The result is the number of cells for which no one of two diagonals crossing it is occupied by cats. This solution has time complexity O(N^2) and while it allows us to solve more testcases than O(N^3) solution, it is still to slow to pass all tests.
Since N can be as big as 10^6, we have to avoid iterating over all grid cells, if we want to speed up our solution. Notice that, if we are able to count the number of cells occupied by cats, we can easily get the result by subtracting this number from N \cdot N - the total number of cells. The first step here is the same as in the O(N^2) method - we iterate over input cells marking diagonals which are full of cats.
From now we refer to diagonal as a diagonal which is marked as being full of cats.
Notice that we can easily get the number of cells crossed by a diagonal (left or right), if we know the number assigned to this diagonal. In our case, we can use the equation below to get the number of cells crossed by a diagonal (both left and right) for a given id number assigned to diagonal:
Based on the above equation, we can iterate over all diagonals and count the total number of cells in these diagonals. Let T be that number.
Everything looks fine right now, but we might take into account too many cells. For example, a left and a right diagonal may cross each other, and we count this crossed cell exactly two times in T. In order to get the final result, we have to subtract the number of cells which are crossed by two diagonals full of cats from T.
How to get the number of cells which are crossed by two diagonals? Notice that a left diagonal cannot cross another left diagonal. This is true for right diagonals also. So for each right diagonal, we want to get the number of left diagonals which cross it.
If you take a closer look at a right diagonal with number K assigned to it, you will notice that it crosses some left diagonals with even numbers assigned to them if and only if K is even too. Otherwise it crosses some left diagonals with odd number assigned to them.
Let K be a number assigned to a right diagonal, then if K \leq N, it crosses all left diagonals with numbers in range [N - K + 1, N + K - 1] with the same parity as K.
Otherwise, if K \gt N, let X = 2 \cdot N - K. Then this diagonal crosses all left diagonals with numbers in range [N - X + 1, N + X - 1] and same parity as K.
So the only thing to do is to get the number of diagonals with even/odd numbers assigned to them is some range [A, B] which are full of cats. How to do that? Well, we can use prefix sums to do that. Precisely, compute the number of diagonals with even/odd numbers assigned to them in range [1, B] for each 1 \leq B \leq 2 \cdot N - 1. Let oddPrefix[B] and evenPrefix[B] represent this prefix sums. Then in order to get the number of, let’s say odd, diagonals which are full of cats in a range [A, B], we just compute oddPrefix[B] - oddPrefix[A - 1].
The total complexity of this method is O(K + N), because in the first step, we iterate over all input cells and in the second step we iterate a few times over all diagonals, and there are O(N) diagonals.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
