Problem Link:
Author: Pavel Sheftelevich
Tester: Kanstantsin Sokal
Editorialist: Sunny Aggarwal
Difficulty:
Medium
Pre-Requisites:
Strings, Polynomial Hashing, Binary Search, Implementation, Palindromes.
Problem Statement:
A string is considered to be a K palindromic string if it can be converted to a usual palindrome by replacing no more than K characters. Given a string S, find the sum of length of all K - palindromic substrings of it.
Brief Explanation:
Calculate the sum of lengths of odd length K-palindromes and even length K-palindromes separately. Calculation for the sum of lengths of even length K-palindromes is identical to the calculation of sum of lengths of odd length K-palindromes. Sum of lengths of odd length K-palindromes can be found by fixing the center of the palindrome and then finding the pair of unequal characters K times at equal length from the center of palindrome on both side of center. This can be using binary search and hashing in O(NKlog(N)).
Solution:
As explained above, it is best to consider odd length K-plaindromes and even length K-plaindromes separately.
How to compute sum of lengths of odd length K-palindromes ?
Let us consider an example where
N = 5, K = 1
S="RADRRD"
We will consider all the characters from 1 to N one by one and treat them as a center of our K-palindrome.
Case 1: 1^{st} character as a center.

Note that this palindrome cannot be extended on left side of center and therefore there is only 1 K-plaindrome i.e "R".
case 2: 2^{nd} character as a center.
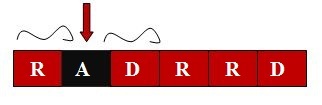
With 2^{nd} character as center there are 2 possible candidates for K-palindrome i.e "A" and "RAD". "A" is already a K-palindrome and "RAD" can be converted to a palindrome by changing at most 1 character either 'R' to 'D' to form "DAD" or 'D' to 'R' to form "RAR".
case 3: 3^{rd} character as a center.
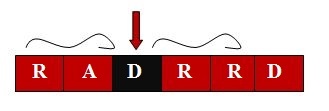
There are 3 possible candidates for K-palindromes i.e "D", "ADR", "RADRR". "D" is already a 1-palindrome, "ADR" can be converted to 1-palindrome, "RADRR" can also be converted to 1-palindrome.
case 4: 4^{th} character as a center.
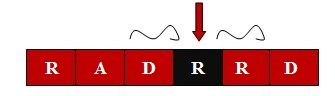
There are 3 possible candidates for K-palindromes i.e "R", "DRR", "ADRRD". "R" is already a 1-palindrome, "DRR" can be converted to 1-palindrome, “ADRRD” can’t be converted to 1-palindrome as it requires more than 1 character replacement to be a palindrome.
case 5: 5^{th} character as a center.
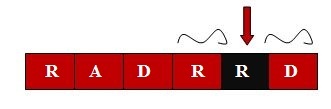
There are only 2 possible candidates for K-palindromes i.e "R" and "RRD". "R" is already a 1-palindrome, "RRD" can be converted to 1-palindrome.
case 6: 6^{th} character as a center.
There are only 1 possible candidates for K-palindromes i.e "D" and it is already a 1-palindrome.
It is easy to notice from above that for each center, we are finding the maximum length X such that X characters on the left of center + center + X characters on the right of center together forms K-palindrome. This can be done efficiently using binary search on X and hashing. A very good tutorial on hashing along with its usage in many different kind of problems is available here and here.
Using binarysearch we will find the first mismatch across the center and correct it by changing the hash value, then we will find the next mismatch and correct it and so on upto K times.
There are N possible centers of odd palindromes and we are applying K times binary search on each center. Therefore, the overall complexity of calculating sum of lengths of odd length K palindrome is NKlog(N).
Note that calculating sum of lengths of even length K-palindrome is almost identical to what explained above.
Please have a look at author’s solution & tester’s solution for implementation details.
Time Complexity:
O(NKlog(N))
Space Complexity:
O(N)
Similiar Problems:
Solution:
Setter’s solution can be found here
Tester’s solution can be found here
Feel free to post comments if anything is not clear to you.
