PROBLEM LINK:
Setter: Mladen Puzic
Tester: Michael Nematollahi
Editorialist: Taranpreet Singh
DIFFICULTY:
PREREQUISITES:
Mo’s algorithm on tree or Heavy-Light Decomposition, Randomization.
PROBLEM:
You are given a tree with N nodes, where a value is assigned to each node, given in array A. You have to process following updates and queries.
- Update value assigned to node p to X.
- Consider all values assigned nodes on the path from L to R on the path from u to v. Say the number of nodes is L. Print Yes, if the values under consideration form a permutation of natural numbers in the range [1, L].
EXPLANATION
First of all, assign random numbers > 0 to each value from 1 to N and for each value in the array A, replace x by the random value assigned to x.
Let us consider we need to answer query (u, v) such that there are L nodes on the path from u to v. Consider the xor of all values on the path from u to v. If the values on path form a permutation of first L natural numbers, then this xor value shall be equal to the xor of values assigned to each i from 1 to L. Xor of values assigned from 1 to i can be easily precomputed using prefix xor for each i from 1 to N. So, the answer to our query becomes Yes, if the xor of numbers on the path from u to v is the prefix xor up to position L.
This gives us the means to check if values of nodes on a path form the permutation or not, if we can somehow implement a data structure capable of updating value for a position, and finding xor of values on a path.
We can either use Heavy-Light Decomposition but there’s a simpler and efficient solution using Euler tour and Mo’s algorithm on trees.
Since the inverse of xor operation is xor operation itself, we can see, that xoring with a number twice doesn’t affect the initial value.
Consider the sample tree as given below.
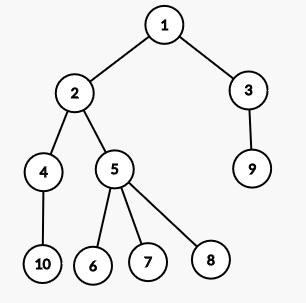
The Euler tour for this Tree shall be
1 2 4 10 10 4 5 6 6 7 7 8 8 5 2 3 9 9 3 1
We can see, that for query (u, v) (Assuming ST_u \leq ST_v where ST denote start times and EN denote end times.), if LCA of u and v is u, then interval [ST_u, ST_v] contains all nodes on path from u to v exactly once, while all other nodes either twice or not at all (ST being . Since xor operation cancels itself, presence of any node twice negates its presence, and we are only left with nodes on the path from u to v. This way, we can get xor of value on the path from u to v as xor of an interval.
Similarly, if LCA of u and v is not u, we need to consider LCA node separately, and remaining nodes on the path from u to v appear exactly once in the interval [EN_u, ST_v].
For updates, we just need to update the start and end position of a node with the random value assigned to value given in update in the segment tree.
TIME COMPLEXITY
Time complexity is O((N+Q)*log(N)) per test case.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
#define STIZE(x) fprintf(stderr, "STIZE%d\n", x);
#define PRINT(x) cerr << #x << ' ' << x << endl;
#define NL(x) printf("%c", " \n"[(x)]);
#define lld long long
#define pll pair<lld,lld>
#define pb push_back
#define fi first
#define se second
#define mid (l+r)/2
#define endl '\n'
#define all(a) begin(a),end(a)
#define sz(a) int((a).size())
#define LINF 2000000000000000000LL
#define INF 1000000000
#define EPS 1e-9
using namespace std;
#define MAXN 500010
#define MAXL 20
mt19937 rng(48201);
vector<int> adj[MAXN];
int N, Q, in[MAXN], out[MAXN], dub[MAXN], anc[MAXN][MAXL], timer;
unsigned lld bit[2*MAXN], prefix[MAXN], val[MAXN];
map<int, unsigned lld> hsh;
map<unsigned lld, bool> used;
void update(int idx, unsigned lld val) {
while(idx < 2*MAXN) {
bit[idx] ^= val;
idx += idx&-idx;
}
}
unsigned lld query(int idx) {
unsigned lld xorr = 0;
while(idx) {
xorr ^= bit[idx];
idx -= idx&-idx;
}
return xorr;
}
unsigned lld query(int l, int r) {
return query(r)^query(l-1);
}
void dfs(int node, int prev, int dubb) {
dub[node] = dubb;
in[node] = ++timer;
anc[node][0] = prev;
for(auto x : adj[node]) {
if(x != prev) dfs(x, node, dubb+1);
}
out[node] = ++timer;
}
void initLCA(int node) {
dfs(1, 1, 0);
for(int i = 1; i <= N; i++) update(in[i], val[i]), update(out[i], val[i]);
for(int d = 1; d < MAXL; d++) {
for(int i = 1; i <= N; i++) {
anc[i][d] = anc[anc[i][d-1]][d-1];
}
}
}
bool inSubtree(int X, int Y) { ///Y in subtree of X
return (in[X] <= in[Y] && out[Y] <= out[X]);
}
int LCA(int X, int Y) {
if(inSubtree(X, Y)) return X;
if(inSubtree(Y, X)) return Y;
for(int d = MAXL-1; d >= 0; d--) {
if(!inSubtree(anc[X][d], Y)) X = anc[X][d];
}
return anc[X][0];
}
unsigned long long getRand() {
unsigned lld x;
while(1) {
x = uniform_int_distribution<unsigned lld> (1, ULLONG_MAX)(rng);
if(!used[x]) {
used[x] = true;
return x;
}
}
}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cerr.tie(0);
int T; cin >> T;
while(T--) {
hsh.clear(); used.clear(); timer = 0;
cin >> N >> Q;
for(int i = 1; i <= N; i++) prefix[i] = 0, adj[i].clear();
for(int i = 1; i <= 2*N; i++) bit[i] = 0;
for(int i = 1; i <= N; i++) {
hsh[i] = getRand();
prefix[i] = prefix[i-1] ^ hsh[i];
}
for(int i = 1; i <= N; i++) {
cin >> val[i];
if(hsh[val[i]] == 0) hsh[val[i]] = getRand();
val[i] = hsh[val[i]];
}
for(int i = 1; i < N; i++) {
int x, y; cin >> x >> y;
adj[x].pb(y);
adj[y].pb(x);
}
initLCA(1);
while(Q--) {
int type, X, Y; cin >> type >> X >> Y;
if(type == 1) {
if(in[Y] < in[X]) swap(X, Y);
int lca = LCA(X, Y);
int L = dub[X] + dub[Y] - 2*dub[lca] + 1;
unsigned lld rez = 0;
if(X == lca) rez = query(in[X], in[Y]);
else rez = query(out[X], in[Y]) ^ val[lca];
if(rez == prefix[L]) cout << "Yes\n";
else cout << "No\n";
} else {
if(hsh[Y] == 0) hsh[Y] = getRand();
unsigned lld y = hsh[Y];
update(in[X], y^val[X]);
update(out[X], y^val[X]);
val[X] = y;
}
}
}
}
Tester's Solution
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef pair<int, int> pii;
#define F first
#define S second
#define tm kljasdf
const int MAXN = 5e5 + 10;
const int B[2] = {690397, 692141};
int n, q, a[MAXN];
vector<int> adj[MAXN];
ull pw(ull a, int b){
ull ret = 1;
while (b){
if (b & 1)
ret = ret*a;
b >>= 1;
a = a*a;
}
return ret;
}
int sub[MAXN], depth[MAXN], par[MAXN];
bool cmp(int u, int v){return sub[u] > sub[v];}
void plant(int v, int p = -1, int de = 0){
if (~p)
adj[v].erase(find(adj[v].begin(), adj[v].end(), p));
sub[v] = 1;
depth[v] = de;
par[v] = p;
for (int u:adj[v]) {
plant(u, v, de+1);
sub[v] += sub[u];
}
sort(adj[v].begin(), adj[v].end(), cmp);
}
int curRt = -1, root[MAXN], st[MAXN], tm, ord[MAXN];
void hld(int v){
if (curRt == -1)
curRt = v;
root[v] = curRt;
ord[tm] = v;
st[v] = tm++;
for (int u:adj[v]){
hld(u);
curRt = -1;
}
}
ull seg[MAXN<<2][2];
void merge(int v){
for (int w = 0; w < 2; w++)
seg[v][w] = seg[v<<1][w] + seg[v<<1^1][w];
}
void reCalc(int v, int val){
for (int w = 0; w < 2; w++)
seg[v][w] = pw(B[w], val);
}
void plantSeg(int v, int b, int e){
if (e - b == 1){
reCalc(v, a[ord[b]]);
return;
}
int mid = b + e >> 1;
plantSeg(v<<1, b, mid);
plantSeg(v<<1^1, mid, e);
merge(v);
}
void upd(int v, int b, int e, int pos){
if (e - b == 1){
reCalc(v, a[ord[pos]]);
return;
}
int mid = b + e >> 1;
if (pos < mid)
upd(v<<1, b, mid, pos);
else
upd(v<<1^1, mid, e, pos);
merge(v);
}
pair<ull, ull> getSeg(int v, int b, int e, int l, int r){
if (l <= b && e <= r) return {seg[v][0], seg[v][1]};
if (r <= b || e <= l) return {0, 0};
int mid = b + e >> 1;
auto x = getSeg(v<<1, b, mid, l, r);
auto y = getSeg(v<<1^1, mid, e, l, r);
return {x.F+y.F, x.S+y.S};
}
pair<pair<ull, ull>, int> get(int u, int v){
pair<pair<ull, ull>, int> ret = {{0, 0}, 0};
while (root[u] ^ root[v]){
if (depth[root[u]] < depth[root[v]])
swap(u, v);
ret.S += depth[u] - depth[root[u]] + 1;
auto x = getSeg(1, 0, n, st[root[u]], st[u]+1);
ret.F.F += x.F, ret.F.S += x.S;
u = par[root[u]];
}
if (depth[u] < depth[v])
swap(u, v);
ret.S += depth[u] - depth[v] + 1;
auto x = getSeg(1, 0, n, st[v], st[u]+1);
ret.F.F += x.F, ret.F.S += x.S;
return ret;
}
ull sv[MAXN][2];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
for (int i = 1; i < MAXN; i++)
for (int w = 0; w < 2; w++){
sv[i][w] = sv[i-1][w] + pw(B[w], i);
}
int te; cin >> te;
while (te--){
cin >> n >> q;
for (int i = 0; i < n; i++) adj[i].clear();
tm = 0;
curRt = -1;
for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i < n-1; i++){
int a, b; cin >> a >> b, a--, b--;
adj[a].push_back(b);
adj[b].push_back(a);
}
plant(0);
hld(0);
plantSeg(1, 0, n);
while (q--){
int type; cin >> type;
if (type == 1){
int u, v; cin >> u >> v, u--, v--;
auto x = get(u, v);
if (sv[x.S][0] != x.F.F || sv[x.S][1] != x.F.S)
cout << "No\n";
else
cout << "Yes\n";
}
else{
int v, val; cin >> v >> val, v--;
a[v] = val;
upd(1, 0, n, st[v]);
}
}
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
class QRYLAND{
//SOLUTION BEGIN
int B = 20;
void pre() throws Exception{}
void solve(int TC) throws Exception{
int n = ni(), q = ni();
int[] a = new int[n];
for(int i = 0; i< n; i++){
a[i] = ni();
if(a[i] > n)a[i] = 0;
}
int[] rand = new int[1+n];
Random r = new Random();
for(int i = 1; i<= n; i++)rand[i] = 1+r.nextInt((1<<30)-1);
int[] pre = new int[1+n];
for(int i = 1; i<= n; i++)pre[i] = pre[i-1]^rand[i];
int[][] e = new int[n-1][];
for(int i = 0; i< n-1; i++)e[i] = new int[]{ni()-1, ni()-1};
int[][] g = makeU(n, e);
time = -1;
int[] depth = new int[n];
int[][] par = new int[B][n];
for(int b = 0; b < B; b++)Arrays.fill(par[b], -1);
int[] eu = new int[2*n];
int[][] ti = new int[n][2];
dfs(g, ti, eu, par, depth, 0, -1);
for(int i = 0; i< 2*n; i++)eu[i] = rand[a[eu[i]]];
SegTree t = new SegTree(eu);
while(q-->0){
int ty = ni();
if(ty == 1){
int x = ni()-1, y = ni()-1;
int lca = lca(par, depth, x, y);
if(ti[x][0] > ti[y][0]){
int tt = x;
x = y;
y = tt;
}
if(lca == x){
int xor = t.q(ti[x][0], ti[y][0]);
int length = depth[x]+depth[y]-2*depth[lca]+1;
pn(xor == pre[length]?"Yes":"No");
}else{
int xor = t.q(ti[x][1], ti[y][0])^t.q(ti[lca][0], ti[lca][0]);
int length = depth[x]+depth[y]-2*depth[lca]+1;
pn(xor == pre[length]?"Yes":"No");
}
}else{
int x = ni()-1, y = ni();
int rnd = 0;
if(1<= y && y<= n)rnd = rand[y];
t.u(ti[x][0], rnd);
t.u(ti[x][1], rnd);
}
}
}
int lca(int[][] par, int[] d, int u, int v){
if(d[u] > d[v]){
int t = u;
u = v;
v = t;
}
for(int b = B-1; b>= 0; b--)if((((d[v]-d[u])>>b)&1) == 1)v = par[b][v];
if(u == v)return u;
for(int b = B-1; b>= 0; b--)
if(par[b][u] != par[b][v]){
u = par[b][u];
v = par[b][v];
}
return par[0][u];
}
int time;
void dfs(int[][] g, int[][] ti, int[] eu, int[][] par, int[] d, int u, int p){
par[0][u] = p;
for(int b = 1; b< B; b++)
if(par[b-1][u] != -1)
par[b][u] = par[b-1][par[b-1][u]];
eu[++time] = u;
ti[u][0] = time;
for(int v:g[u])if(v!= p){
d[v] = d[u]+1;
dfs(g, ti, eu, par, d, v, u);
}
eu[++time] = u;
ti[u][1] = time;
}
class SegTree{
int m= 1;
int[] t;
public SegTree(int[] a){
while(m<a.length)m<<=1;
t = new int[m<<1];
for(int i = 0; i< a.length; i++)t[i+m] = a[i];
for(int i = m-1; i>0; i--)t[i] = t[i<<1]^t[i<<1|1];
}
void u(int p, int value){
t[p+=m] = value;
for(p>>=1;p>0;p>>=1)t[p] = t[p<<1]^t[p<<1|1];
}
int q(int l, int r){
int ans = 0;
for(l+=m,r+=m+1;l<r;l>>=1,r>>=1){
if((l&1)==1)ans^=t[l++];
if((r&1)==1)ans^=t[--r];
}
return ans;
}
}
int[][] makeU(int n, int[][] edge){
int[][] g = new int[n][];int[] cnt = new int[n];
for(int i = 0; i< edge.length; i++){cnt[edge[i][0]]++;cnt[edge[i][1]]++;}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< edge.length; i++){
g[edge[i][0]][--cnt[edge[i][0]]] = edge[i][1];
g[edge[i][1]][--cnt[edge[i][1]]] = edge[i][0];
}
return g;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
DecimalFormat df = new DecimalFormat("0.00000000000");
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new QRYLAND().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to Share your approach, if you want to. (even if its same ![]() ) . Suggestions are welcomed as always had been.
) . Suggestions are welcomed as always had been. ![]()
